
- •«Российская таможенная академия»
- •План чтения лекции №1
- •«Российская таможенная академия»
- •Понятие «эконометрика»
- •Формулировки определений понятия «эконометрика»
- •Задачи эконометрики
- •Эконометрическая модель
- •Задачи эконометрическoго моделирования
- •Классы эконометрических моделей
- •Типы данных и виды переменных в эконометрическом моделировании Типы данных
- •Виды переменных
- •Этапы эконометрического моделирования
- •Модели парной регрессии
- •Множественная регрессия. Мультиколлинеарность данных
- •3.2. Отбор факторов при построении множественной регрессии
- •3.2.1. Требования к факторам
- •3.2.2. Мультиколлинеарность
- •3.3. Выбор формы уравнения регрессии
- •3.4. Оценка параметров уравнения линейной
- •3.5. Качество оценок мнк линейной множественной регрессии. Теорема Гаусса-Маркова
- •3.6. Проверка качества уравнения регрессии. F-критерий Фишера
- •3.7. Точность коэффициентов регрессии. Доверительные интервалы
- •3.8 Прогнозирование по модели множественной регрессии
- •3.9 Гетероскедастичность случайных остатков
- •3.10. Обобщенный метод наименьших квадратов
- •3.11. Фиктивные переменные
- •3.12. Тест Чоу
- •Системы одновременных уравнений
- •4.1. Структурная и приведённая форма модели
- •4.2. Оценивание параметров структурной модели
- •Методы оценивания структурных уравнений различных видов
- •1. Точная идентифицируемость
- •2.Сверхидентифицируемость
- •3.Неидентифицируемость
- •Порядковое условие идентификации
- •Ненулевое ограничение
- •3. Анализ методов оценивания
- •Моделирование изолированного динамического ряда
- •Компоненты динамического ряда
- •Выявление и характеристика основной тенденции развития
- •Экспоненциальное сглаживание.
- •Моделирование основной тенденции
- •Статистическое изучение сезонных колебаний
- •Автокорреляция уровней динамического ряда и характеристика его структуры
- •3; 1; 2; 1; 2; 1; 3; 3; 2; 3; 1; 2; 1; 1; 3; 3; 2; 2; 1; 3; 3; 2; 2; 3; 1; 2; 2; 1; 3; 1.
- •Специфика изучения взаимосвязей по рядам динамики
- •Методы исключения тенденции
- •Метод последовательных разностей
- •Метод отклонений от тренда
- •Включение в модель регрессии фактора времени
- •Обобщенный метод наименьших квадратов при построении модели регрессии по временным рядам
- •Модели с лаговыми переменными
- •Модели с распределенными лагами
- •Метод Койка
- •Модели авторегрессии
- •Интерпретация параметров модели авторегрессии
- •Инструментальные переменные как метод оценивания параметров модели авторегрессии
- •Оценка автокорреляции остатков по модели авторегрессии
- •Авторегрессионные процессы и их моделирование (общая характеристика) Авторегрессионные процессы
- •Модели скользящей средней
- •Модели arma
- •Модели arima
- •Методология построения модели arima для исследуемого временного ряда включает следующую последовательность шагов.
- •Кластерный анализ
Модели с лаговыми переменными
Общая характеристика
До сих пор рассматривались модели по
временным рядам, в которых
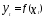 .
Между тем в моделях временных рядов
зависимая переменная
.
Между тем в моделях временных рядов
зависимая переменная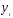 может быть связана не только со значениями
объясняющих переменныххв
момент времениt, но и с их
значениями в предыдущие моменты времени.
Так, например, потребление товаров
длительного пользования зачастую
зависит от доходов не только текущего,
но и предыдущих периодов. Аналогично
величина основных производственных
фондов зависит от размера инвестиций
не только текущего года, но и предыдущих
лет. В этом случае строятся модели с
лаговыми объясняющими переменными.
Например,
может быть связана не только со значениями
объясняющих переменныххв
момент времениt, но и с их
значениями в предыдущие моменты времени.
Так, например, потребление товаров
длительного пользования зачастую
зависит от доходов не только текущего,
но и предыдущих периодов. Аналогично
величина основных производственных
фондов зависит от размера инвестиций
не только текущего года, но и предыдущих
лет. В этом случае строятся модели с
лаговыми объясняющими переменными.
Например,
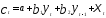 ,
(5.32)
,
(5.32)
где
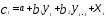 — потребление в период времениt;
— потребление в период времениt;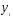 —
доход в период времениt;
—
доход в период времениt;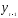 — доход в предыдущий периодt - 1.
— доход в предыдущий периодt - 1.
В данной модели лаговой является
переменная
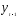 ,
т.е. доход за предыдущий период времени.
Возможна ситуация, когда объясняющая
переменнаяхвлияет на результатуне сразу же, а с определенным
запаздыванием во времени, превышающем
один временной интервал. Так, выпуск
специалистов высшей квалификации
зависит от приема в вузы четырех- или
пятилетней давности.
,
т.е. доход за предыдущий период времени.
Возможна ситуация, когда объясняющая
переменнаяхвлияет на результатуне сразу же, а с определенным
запаздыванием во времени, превышающем
один временной интервал. Так, выпуск
специалистов высшей квалификации
зависит от приема в вузы четырех- или
пятилетней давности.
Объясняющие переменные, взятые в модели
регрессии с запаздыванием во времени,
называются лаговыми переменными.
Величина интервала запаздывания
называется лагом. Так, в модели
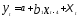 ,
лаговая переменнаяхвзята с
лагом, равным четыре.
,
лаговая переменнаяхвзята с
лагом, равным четыре.
Вместе с тем в правой части модели лаговой переменной может быть и зависимая переменная. Например, спрос на товар может зависеть не только от дохода, но и от достигнутого спроса на него в предыдущий период времени. Или ставка банковского кредита может зависеть не только от объема денежной массы в наличии, но и от достигнутого ранее процента банковского кредита. В этом случае строятся модели с лаговой зависимой переменной. Например,
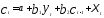 ,
(5.33)
,
(5.33)
где
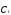 — потребление в период времениt;
— потребление в период времениt;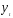 — доход в период времени t;
— доход в период времени t;
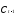 — потребление в предыдущий период
времениt - 1.
— потребление в предыдущий период
времениt - 1.
Модели регрессии по временным рядам с лаговыми переменными принято называть динамическими моделями. Их можно подразделить на три класса
1. Модели с лаговыми объясняющими переменными — модели с распределенными лагами
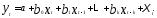 (5.34)
(5.34)
2. Модели с лаговыми зависимыми переменными — модели авторегрессии
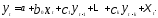 5.35)
5.35)
3. Модели с лаговыми зависимыми и независимыми переменными — авторегрессионные модели с распределенными лагами
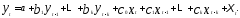 (5.36)
(5.36)
Центральным вопросом при построении
моделей с лаговыми переменными является
выбор величины лага и числа лаговых
переменных. Теоретически трудно
определить величину лага. Определенную
помощь может оказать взаимная
корреляционная функция: рассчитывается
множество коэффициентов корреляции
между уровнями временных рядов
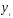 и
и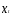 ,
сдвинутыми относительно друг друга на
последовательно увеличивающиеся
интервалы времени. Величина лага
определяется по максимальному значению
коэффициента корреляции. Например,
продажа товара за две декады двумя
филиалами фирмы характеризуется
данными, представленными в таблице
(тыс. ден. ед.).
,
сдвинутыми относительно друг друга на
последовательно увеличивающиеся
интервалы времени. Величина лага
определяется по максимальному значению
коэффициента корреляции. Например,
продажа товара за две декады двумя
филиалами фирмы характеризуется
данными, представленными в таблице
(тыс. ден. ед.).
|
Числа месяца |
Филиал № 1 |
Филиал № 2 |
Числа месяца |
Филиал № 1 |
Филиал № 2 |
|
1 |
5 |
9 |
11 |
9,5 |
13 |
|
2 |
4,5 |
10,8 |
12 |
8 |
14 |
|
3 |
4 |
13,5 |
13 |
7,6 |
15 |
|
4 |
4,1 |
14,5 |
14 |
7,5 |
20 |
|
5 |
5 |
16 |
15 |
7,6 |
24 |
|
6 |
7 |
14,7 |
16 |
10 |
25 |
|
7 |
8 |
14 |
17 |
12,2 |
26 |
|
8 |
9,7 |
12 |
18 |
15 |
26,3 |
|
9 |
10 |
11,9 |
19 |
15,6 |
26,4 |
|
10 |
11 |
12 |
20 |
16 |
27,1 |
Примем объем продаж филиалом № 1 за
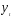 ,
а филиалом № 2 — за
,
а филиалом № 2 — за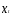 .
Если прокоррелировать
.
Если прокоррелировать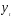 и
и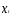 ,
то коэффициент корреляции между ними
составит 0,6912. При последовательном
сдвиге уровней ряда
,
то коэффициент корреляции между ними
составит 0,6912. При последовательном
сдвиге уровней ряда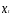 на один временной интервал получатся
коэффициенты корреляции, представленные
в следующей таблице.
на один временной интервал получатся
коэффициенты корреляции, представленные
в следующей таблице.
|
|
|
Величина лага |
|
|
| ||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 | |
|
0,7738 |
0,867 |
0,9445 |
0,9553 |
0,8562 |
0,5977 |
0,0724 | |
Следовательно, объем продаж филиалом
№ 1 в наибольшей мере коррелирует с
объемом продаж по филиалу № 2 с интервалом
в 4 дня. Уравнение регрессии принимает
вид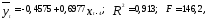 что статистически значимо. Оно позволяет
по данным филиала № 2, взятым на четыре
дня раньше, предсказывать объем продаж
по филиалу № 1. Так, например, при объеме
продаж за 2-е число в 10,8 тыс. ден. ед. по
филиалу № 2 объем продаж по филиалу №
1 составит 6-го числа 7,1 тыс. ден. ед.
Соответственно подставляя в уравнение
регрессии информацию об объеме продаж
филиалом № 2 за 3—16-е числа, получим
объем продаж по филиалу № 1 на 7—20-е
числа.
что статистически значимо. Оно позволяет
по данным филиала № 2, взятым на четыре
дня раньше, предсказывать объем продаж
по филиалу № 1. Так, например, при объеме
продаж за 2-е число в 10,8 тыс. ден. ед. по
филиалу № 2 объем продаж по филиалу №
1 составит 6-го числа 7,1 тыс. ден. ед.
Соответственно подставляя в уравнение
регрессии информацию об объеме продаж
филиалом № 2 за 3—16-е числа, получим
объем продаж по филиалу № 1 на 7—20-е
числа.
Выбор величины лага и количества лагов проводится обычно экспериментально: строятся модели с разным числом лагов и их величиной и изучается значимость коэффициентов регрессии при лаговых переменных; останавливаются на модели, для которой все коэффициенты регрессии при лаговых переменных будут статистически значимыми по t-критерию Стьюдента.
Построение моделей с лаговыми переменными
имеет свою специфику. Дело не только в
выборе величины лага и их числа. Во
многих случаях оценка параметров
моделей с лаговыми переменными не может
быть проведена с помощью традиционного
МНК ввиду нарушения ряда его предпосылок
и требует специальных методов оценивания.
При наличии двух и более лаговых
переменных возникает проблема
мультиколлинеарности факторов, ибо,
как правило,
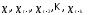 или
или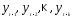 связаны между собой, особенно при
наличии тенденции в рядах динамики.
Это снижает точность оценок коэффициентов
при лаговых переменных и требует
видоизменять приемы оценивания.
связаны между собой, особенно при
наличии тенденции в рядах динамики.
Это снижает точность оценок коэффициентов
при лаговых переменных и требует
видоизменять приемы оценивания.
