Метод отклонений от тренда

Как уже указывалось, метод отклонений от тренда является более точным методом исключения тенденции из данных вре­менного ряда. Это связано не только с тем, что тенденция вы­ражается в виде уравнения тренда любой математической фун­кции. Рассматриваемые для модели регрессии ряды динамики могут иметь разные тенденции. Например, ряд x_tописыва­ется гиперболой, а рядy_t— параболой. В этом случае метод отклонений от тренда позволяет исключить из каждого вре­менного ряда соответствующую ему тенденцию.

Алгоритм построения регрессии при применении метода отклонений следующий.

1. Для каждого временного ряда определяются уравнение тренда и теоретические значения y_t; x_t.

2. По каждому из рядов находятся остаточные величины

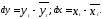
3. Строится модель регрессии

dy = f(dx).(5.17)

В линейной регрессии 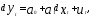парам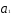етрпоказы­вает как в среднем изменяется величина случайных отклоне­ний по рядуy_tс изменением случайных колебаний рядаx_tна единицу. Если при этом оба ряда характеризуются линейной тенденцией, то параметр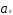= 0, так как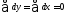. Тогда модель линейной регрессии примет вид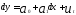и пара­метр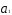будет выступать коэффициентом пропорциональнос­ти. Его величина будет показывать, во сколько раз случайные отклонения по рядуy_tв среднем выше (ниже) случайных от­клонений по рядуx_t.

Для прогноза конкретных значений можно перейти к урав­нению, связывающему между собой уровни временных ря­дов. С этой целью в модель регрессии 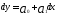подставим значенияdyиdx,раскрыв их содержание, т.е.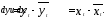

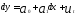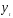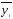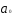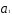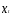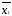Тогда имеем, например, для линейной регрессии , т.е.- = +(-),или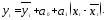

Данную модель можно использовать для прогноза

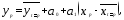(5.18)

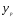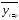где —прогнозное значение у;—прогнозупо тренду приt=р; х_р— прогнозное значениех,найденное либо по модели рег­рессии, либо как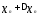;x_t=p— прогнозхисходя из уравнения тренда приt = р.

Результат прогноза зависит от качества прогноза фактора хи от качества трендовых моделей, используемых в прогно­зировании.

Включение в модель регрессии фактора времени

Модель регрессии по двум временным рядам с включением в нее как отдельной независимой переменнойфактора вре­мени tимеет вид

y = a+bx+ct+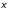, (5.19)

гдеt = 1, 2,3,..., п.

Включая в регрессию фактор времени t,устраняем линей­ную тенденцию из уровней временных рядов. Это объясня­ется спецификой множественной регрессии: коэффициенты регрессии показывают изолированное влияние на результат соответствующего фактора при неизменном уровне других факторов. В (5.19) коэффициент регрессииbхарактеризует «чистое» воздействие переменнойхна результатув условиях неизмен­ной тенденции, т.е. при ее устранении.

Математически доказано, что если временные ряды характеризуются линейной тенденцией, то включение в модель фак­тора времени tравносильно построению модели регрессии по отклонениям от трендов с последующим переходом от нее к исходным уровням временного ряда зависимой переменнойу.

В регрессии y_t=a + bx + ctпараметрbпоказывает, на сколь­ко единиц изменяется в среднемупри изменениихна одну единицу в условиях неизменной тенденции; параметрспока­зывает средний абсолютный приростув условиях неизменно­го уровня объясняющей переменнойх.

Принцип введения в модель фактора времени сохраняется и при изуче­нии трех и более связанных рядов динамики. Так, если стро­ится регрессия у=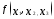, то включение в нее фактора времениtприводит чаще всего к модели вида

y_t=a + b₁x₁+b₂x₂+b₃x₃+ct.

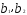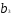В ней параметры ипоказывают изолированное воздействие каждой объясняющей переменной на результату,а параметрс— средний абсолютный приростув условиях неизменности значений переменных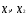и.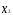

Время в качестве независимой переменной часто вводит­ся в виде линейного члена даже если другие переменные под­вергаются логарифмированию или иному преобразованию.

Например, производственная функция с включением факто­ра времени часто записывается как

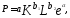
где Р —объем продукции; К—основной капитал;L—занятость;е— основание натурального логарифма;t— фактор времени, взя­тый как ряд натуральных чисел 1,2,...,п.

Если тенденция в рядах динамики характеризуется полиномом второй и более высоких степеней, то в модель регрессии вводятся tиt², а иногдаtв более высокой степени.

В этом случае рассматривается регрессия вида

у = a+bx+ct+dt²(5.20)

при двух временных рядах

или 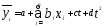(5.21)

при рвременных рядах.

Вводя в модель регрессии фактор времени в виде t, t²,...,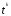, предполагаем, что коэффициенты при переменных остаются во времени неизменными и характеризуют силу связи резуль­татаус соответствующей объясняющей переменнойх.

Если предполагается, что в регрессии коэффициенты при независимой переменной подвержены изменению во времени, то в модель можно ввести преобразованные переменные tx(гдеt— время). Оценка параметров модели дается МНК.

Модель регрессии с включением в нее фактора времени как независимой переменной не всегда эффективна ввиду возможной мультиколлинеарности факторов. Если времен­ные ряды, используемые в регрессии, характеризуются четкой тенденцией (R²>0,9), то корреляцияtи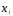может превышать корреляцию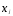су, и параметры регрессии при объясняющих переменныххоказываются ненадежными и экономически не интерпретируемыми.

Время может быть учтено в регрессии и через использова­ние лаговых переменных, т.е. запаздывающих переменных, сдвинутых на определенный интервал времени. Например, спрос на недвижимость в значительной мере определяется до­ходом не текущего, а предыдущих периодов.

Рассмотренные пути учета тенденции при построении мо­дели регрессии по временным рядам не всегда дают желаемые результаты. Регрессия по отклонениям от тренда зачастую име­ет низкий показатель детерминации. Регрессия с включением фактора времени нередко сводится лишь к модели тенденции ввиду статистической незначимости коэффициентов регрессии при объясняющих переменных. Но даже при статистической зна­чимости модели регрессии и ее параметров может остаться автокоррелированность ошибок. Одним из методов ее устранения является обобщенный метод наименьших квадратов.