
- •«Российская таможенная академия»
- •План чтения лекции №1
- •«Российская таможенная академия»
- •Понятие «эконометрика»
- •Формулировки определений понятия «эконометрика»
- •Задачи эконометрики
- •Эконометрическая модель
- •Задачи эконометрическoго моделирования
- •Классы эконометрических моделей
- •Типы данных и виды переменных в эконометрическом моделировании Типы данных
- •Виды переменных
- •Этапы эконометрического моделирования
- •Модели парной регрессии
- •Множественная регрессия. Мультиколлинеарность данных
- •3.2. Отбор факторов при построении множественной регрессии
- •3.2.1. Требования к факторам
- •3.2.2. Мультиколлинеарность
- •3.3. Выбор формы уравнения регрессии
- •3.4. Оценка параметров уравнения линейной
- •3.5. Качество оценок мнк линейной множественной регрессии. Теорема Гаусса-Маркова
- •3.6. Проверка качества уравнения регрессии. F-критерий Фишера
- •3.7. Точность коэффициентов регрессии. Доверительные интервалы
- •3.8 Прогнозирование по модели множественной регрессии
- •3.9 Гетероскедастичность случайных остатков
- •3.10. Обобщенный метод наименьших квадратов
- •3.11. Фиктивные переменные
- •3.12. Тест Чоу
- •Системы одновременных уравнений
- •4.1. Структурная и приведённая форма модели
- •4.2. Оценивание параметров структурной модели
- •Методы оценивания структурных уравнений различных видов
- •1. Точная идентифицируемость
- •2.Сверхидентифицируемость
- •3.Неидентифицируемость
- •Порядковое условие идентификации
- •Ненулевое ограничение
- •3. Анализ методов оценивания
- •Моделирование изолированного динамического ряда
- •Компоненты динамического ряда
- •Выявление и характеристика основной тенденции развития
- •Экспоненциальное сглаживание.
- •Моделирование основной тенденции
- •Статистическое изучение сезонных колебаний
- •Автокорреляция уровней динамического ряда и характеристика его структуры
- •3; 1; 2; 1; 2; 1; 3; 3; 2; 3; 1; 2; 1; 1; 3; 3; 2; 2; 1; 3; 3; 2; 2; 3; 1; 2; 2; 1; 3; 1.
- •Специфика изучения взаимосвязей по рядам динамики
- •Методы исключения тенденции
- •Метод последовательных разностей
- •Метод отклонений от тренда
- •Включение в модель регрессии фактора времени
- •Обобщенный метод наименьших квадратов при построении модели регрессии по временным рядам
- •Модели с лаговыми переменными
- •Модели с распределенными лагами
- •Метод Койка
- •Модели авторегрессии
- •Интерпретация параметров модели авторегрессии
- •Инструментальные переменные как метод оценивания параметров модели авторегрессии
- •Оценка автокорреляции остатков по модели авторегрессии
- •Авторегрессионные процессы и их моделирование (общая характеристика) Авторегрессионные процессы
- •Модели скользящей средней
- •Модели arma
- •Модели arima
- •Методология построения модели arima для исследуемого временного ряда включает следующую последовательность шагов.
- •Кластерный анализ
2.Сверхидентифицируемость
Рассмотрим следующую простую модель Кейнса формирования доходов:
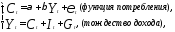 (8)
(8)
где
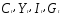 —
объем потребления, совокупный доход,
инвестиции и государственные расходы
соответственно, а
—
объем потребления, совокупный доход,
инвестиции и государственные расходы
соответственно, а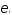 —
случайный член.
—
случайный член.
В исходной модели
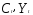 — эндогенные переменные, а
— эндогенные переменные, а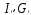 — экзогенные.
— экзогенные.
Разрешая структурную систему относительно эндогенных переменных, получим приведенную систему
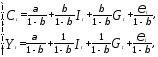 (9)
(9)
Рассмотрим различные методы оценивания
структурных коэффициентов (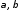 ).
).
Метод инструментальных переменных.
В структурном уравнении функции
потребления в качестве инструментальных
переменных для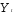 можно использовать как
можно использовать как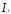 так
и
так
и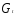 .
Полученные при этом оценки (
.
Полученные при этом оценки (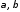 )
будут различаться, но в обоих случаях
они состоятельны.
)
будут различаться, но в обоих случаях
они состоятельны.
Наилучшее решение в данном случае —
применение инструментальной переменной,
которая является комбинацией
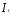 и
и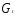 .
.
Структурное уравнение с избыточным числом экзогенных переменных, которые можно использовать как инструментальные, является переопределенным (сверхидентифицируемым).
Двухшаговый метод наименьших квадратов.
Двухшаговый МНК можно рассматривать
как частный случай инструментальных
переменных. В методе ИП было показано,
что структурное уравнение функции
потребления оказалось переопределенным
и сразу две переменные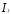 и
и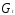 можно
использовать для
можно
использовать для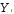 .
.
Однако вместо их раздельного применения
можно предложить их комбинацию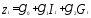 В этом случае требуется оценить значения
коэффициентов
В этом случае требуется оценить значения
коэффициентов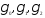 .
.
Фактически вместо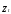 можно использовать оценку
можно использовать оценку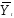 приведенного уравнения
приведенного уравнения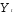 ,
т.е.
,
т.е.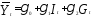 .
.
Подставляя теоретические значения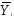 вместо
фактических значений в структурное
уравнение функции потребления, получим
уравнение
вместо
фактических значений в структурное
уравнение функции потребления, получим
уравнение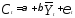 ,
,
которое оценивается обычным МНК. При этом оценки структурных коэффициентов будут состоятельными.
Двухшаговый МНК можно рассматривать как способ конструирования наилучшей из возможных комбинаций инструментальных переменных, если в уравнении имеется избыток экзогенных переменных, которые можно использовать как инструментальные.
Пример 2.Д ля некоторой страны имеются данные о совокупном доходеY, объёме потребленияС, инвестицияхIи государственных расходахG,полученные за 10 лет (усл. ед.):
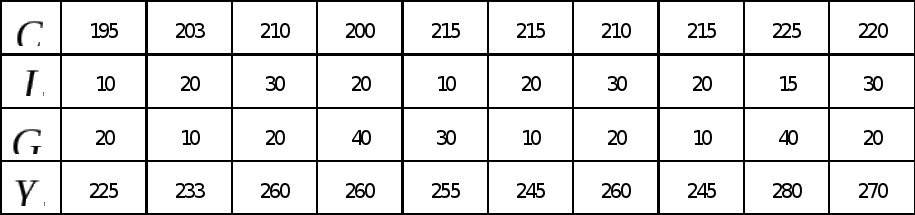
Построим функцию потребления, используя модель Кейнса формирования доходов (8).
Непосредственное оценивание структурного уравнения функции потребления обычным МНК приводит к следующим результатам:
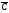 =
109,8 + 0,4Y,
=
109,8 + 0,4Y,
т.е. оценки
 =
109,8,
=
109,8,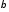 =
0,4.
=
0,4.
Было показано, что исходная модель (8) сверхидентифицируема, поэтому для оценки ее структурных коэффициентов используем ДМНК.
Расчетные значения эндогенной переменной Y, полученные МНК:
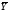 =
201,7 + 1,29I+1,14G.
=
201,7 + 1,29I+1,14G.
Подставим расчетные значения
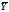 вместо фактических значений в структурное
уравнение функции потребления и оценим
полученное уравнение МНК:
вместо фактических значений в структурное
уравнение функции потребления и оценим
полученное уравнение МНК:
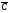 =
171,3 + 0,156Y, т.е. оценки
=
171,3 + 0,156Y, т.е. оценки =
171,3,
=
171,3,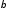 =
0,156.
=
0,156.
Оценки структурных коэффициентов функции потребления, полученные ДМНК, являются состоятельными.
3.Неидентифицируемость
Рассмотрим следующую модель спроса и предложения:
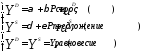
где P- цена товара,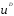 и
и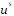 -
случайные члены.
-
случайные члены.
Переменные Y,Рявляются эндогенными, и их значения определяются в процессе установления равновесия.
В рассматриваемой модели нет экзогенных переменных, поэтому ни одно из этих уравнений не является идентифицируемым. Чтобы модель имела статистическое решение, в нее вводятся экзогенные переменные.
Предположим, что продавцы товара облагаются специальным налогом Т, который они должны платить с выручки. При этом уравнение спроса останется неизменным, если переменнаяРозначает рыночную цену, а уравнение предложения изменится:
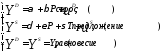 (10)
(10)
где T– экзогенная переменная.
Уравнение спроса будет идентифицируемым, поскольку переменная Тне включена в него и может выступать как инструментальная дляР, а уравнение предложения — неидентифицируемым.
Включим в уравнение спроса экзогенную переменную х— доход на душу населения:
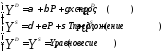 (11)Экзогенную
переменнуюхможно использовать
как инструментальную вместоРдля
уравнения предложения.
(11)Экзогенную
переменнуюхможно использовать
как инструментальную вместоРдля
уравнения предложения.
В итоге получили в целом точно идентифицируемую модель спроса и предложения.
Пусть структурное уравнение спроса имеет временной тренд (скажем, потому что привычки медленно меняются со временем):
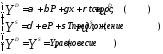 (12)
(12)
где t— переменная
времени, а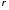 —
коэффициент при ней.
—
коэффициент при ней.
В модели спроса имеются две экзогенные переменные x, t, которые можно использовать в качестве инструментальных дляPв уравнении предложения.
В итоге получили сверхидентифицируемое уравнение предложения и точно идентифицируемое уравнение спроса.
