- •«Российская таможенная академия»
- •План чтения лекции №1
- •«Российская таможенная академия»
- •Понятие «эконометрика»
- •Формулировки определений понятия «эконометрика»
- •Задачи эконометрики
- •Эконометрическая модель
- •Задачи эконометрическoго моделирования
- •Классы эконометрических моделей
- •Типы данных и виды переменных в эконометрическом моделировании Типы данных
- •Виды переменных
- •Этапы эконометрического моделирования
- •Модели парной регрессии
- •Множественная регрессия. Мультиколлинеарность данных
- •3.2. Отбор факторов при построении множественной регрессии
- •3.2.1. Требования к факторам
- •3.2.2. Мультиколлинеарность
- •3.3. Выбор формы уравнения регрессии
- •3.4. Оценка параметров уравнения линейной
- •3.5. Качество оценок мнк линейной множественной регрессии. Теорема Гаусса-Маркова
- •3.6. Проверка качества уравнения регрессии. F-критерий Фишера
- •3.7. Точность коэффициентов регрессии. Доверительные интервалы
- •3.8 Прогнозирование по модели множественной регрессии
- •3.9 Гетероскедастичность случайных остатков
- •3.10. Обобщенный метод наименьших квадратов
- •3.11. Фиктивные переменные
- •3.12. Тест Чоу
- •Системы одновременных уравнений
- •4.1. Структурная и приведённая форма модели
- •4.2. Оценивание параметров структурной модели
- •Методы оценивания структурных уравнений различных видов
- •1. Точная идентифицируемость
- •2.Сверхидентифицируемость
- •3.Неидентифицируемость
- •Порядковое условие идентификации
- •Ненулевое ограничение
- •3. Анализ методов оценивания
- •Моделирование изолированного динамического ряда
- •Компоненты динамического ряда
- •Выявление и характеристика основной тенденции развития
- •Экспоненциальное сглаживание.
- •Моделирование основной тенденции
- •Статистическое изучение сезонных колебаний
- •Автокорреляция уровней динамического ряда и характеристика его структуры
- •3; 1; 2; 1; 2; 1; 3; 3; 2; 3; 1; 2; 1; 1; 3; 3; 2; 2; 1; 3; 3; 2; 2; 3; 1; 2; 2; 1; 3; 1.
- •Специфика изучения взаимосвязей по рядам динамики
- •Методы исключения тенденции
- •Метод последовательных разностей
- •Метод отклонений от тренда
- •Включение в модель регрессии фактора времени
- •Обобщенный метод наименьших квадратов при построении модели регрессии по временным рядам
- •Модели с лаговыми переменными
- •Модели с распределенными лагами
- •Метод Койка
- •Модели авторегрессии
- •Интерпретация параметров модели авторегрессии
- •Инструментальные переменные как метод оценивания параметров модели авторегрессии
- •Оценка автокорреляции остатков по модели авторегрессии
- •Авторегрессионные процессы и их моделирование (общая характеристика) Авторегрессионные процессы
- •Модели скользящей средней
- •Модели arma
- •Модели arima
- •Методология построения модели arima для исследуемого временного ряда включает следующую последовательность шагов.
- •Кластерный анализ
4.2. Оценивание параметров структурной модели
Коэффициенты структурной модели могут быть оценены различными способами в зависимости от вида системы одновременных уравнений. Наибольшее распространение получили следующие методы:
• метод инструментальных переменных (ИП);
• косвенный метод наименьших квадратов (КМНК);
• двухшаговый метод наименьших квадратов (ДМНК).
Методы оценивания структурных уравнений различных видов
1. Точная идентифицируемость
Допустим, требуется оценить параметры уравнения функции потребления в простой модели Кейнса формирования доходов:
 (3)
(3)
где
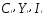 — объем потребления, совокупный доход
и инвестиции соответственно, а
— объем потребления, совокупный доход
и инвестиции соответственно, а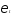 —
случайный член.
—
случайный член.
Структурный коэффициент
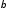 характеризует предельную склонность
к потреблению.
характеризует предельную склонность
к потреблению.
В исходной модели
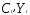 — эндогенные переменные, а
— эндогенные переменные, а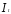 —
экзогенная. Непосредственное оценивание
параметров (
—
экзогенная. Непосредственное оценивание
параметров (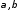 )
в структурном уравнении функции
потребления дает смещенные и
несостоятельные оценки, так как
объясняющая переменная
)
в структурном уравнении функции
потребления дает смещенные и
несостоятельные оценки, так как
объясняющая переменная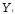 является
эндогенной.
является
эндогенной.
Разрешая структурную систему относительно эндогенных переменных, получим приведенную систему:
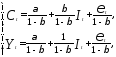 (4)
(4)
В приведенной системе коэффициенты
при переменной
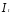 равные
равные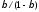 и
и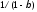 — это инвестиционные мультипликаторы
потребления и дохода соответственно.
Это значит, что если объем инвестиций
возрастет на единицу, то объем потребления
увеличится на
— это инвестиционные мультипликаторы
потребления и дохода соответственно.
Это значит, что если объем инвестиций
возрастет на единицу, то объем потребления
увеличится на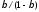 ,
а совокупный доход — на
,
а совокупный доход — на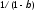 .
.
Рассмотрим различные методы оценивания
структурных коэффициентов
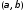 .
.
Косвенный метод наименьших квадратов.
Уравнение для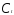 в приведенной форме можно также
представить в виде:
в приведенной форме можно также
представить в виде:
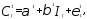 (5)
(5)
где
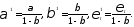 (6)
(6)
В этом уравнении экзогенная переменная
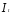 некоррелирована со случайным членом
некоррелирована со случайным членом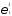 поэтому для оценки параметров (
поэтому для оценки параметров (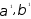 ')
можно использовать обычный МНК.
')
можно использовать обычный МНК.
Замечание. Для удобства рассмотрения оценку параметра и сам параметр будем в дальнейшем обозначать одним символом (параметром).
Оцененное уравнение (5), полученное по выборочным данным с помощью МНК,
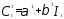 дает
несмещенные и состоятельные оценки
параметров.
дает
несмещенные и состоятельные оценки
параметров.
Из выражения (6) получаем оценки
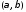 структурных коэффициентов:
структурных коэффициентов:
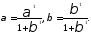 (7)
(7)
Поскольку получены единственные оценки
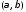 структурных
коэффициентов через оценки (
структурных
коэффициентов через оценки (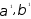 )
приведенных коэффициентов, то структурное
уравнение функции потребления является
однозначно определенным (точно
идентифицируемым).
)
приведенных коэффициентов, то структурное
уравнение функции потребления является
однозначно определенным (точно
идентифицируемым).
Метод инструментальных переменных.Проблема
коррелированности объясняющей переменной
Y, со случайным членом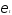 в структурном уравнении (3) для
в структурном уравнении (3) для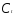 может быть разрешена с помощью метода
ИП.
может быть разрешена с помощью метода
ИП.
Для применения метода ИП необходимо найти такую инструментальную переменную, которая обладает следующими свойствами:
1) коррелирует с неудачно объясняющей
переменной
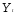 ;
;
2) не коррелирует со случайным членом
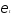 .
.
В данном случае модель сама предоставляет
такую переменную. Величина
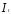 коррелирует с
коррелирует с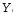 ,
поскольку
,
поскольку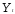 зависит
от
зависит
от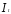 в уравнении (4), и
в уравнении (4), и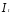 не коррелирует с
не коррелирует с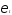 поскольку является экзогенной переменной.
поскольку является экзогенной переменной.
Оценка
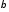 с помощью инструментальной переменной
с помощью инструментальной переменной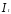 определяется
как
определяется
как
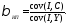
Полученная оценка
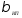 эквивалентна
эквивалентна ,
— оценке
,
— оценке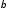 с помощью КМНК. Действительно, из
соотношения (7) и учитывая, что
с помощью КМНК. Действительно, из
соотношения (7) и учитывая, что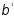 рассчитывается как соv(I,
C)/var(I), получим
рассчитывается как соv(I,
C)/var(I), получим
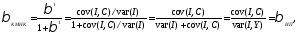
посколькусоv(I, Y) = соv(I,I+ С) = var(I) + cov(I, С).
В общем случае, когда оценка, полученная косвенным методом, единственна, она совпадает с оценкой, полученной методом ИП, т.е. КМНК можно рассматривать как частный случай метода ИП.
Пример 1.Для некоторой страны имеются данные о совокупном доходеY, объеме потребленияСи инвестицияхI, полученные за 10 лет (усл. ед.):
|
|
190 |
198 |
200 |
180 |
200 |
210 |
220 |
210 |
205 |
210 |
|
|
10 |
20 |
30 |
20 |
10 |
20 |
30 |
20 |
15 |
30 |
|
|
200 |
218 |
230 |
200 |
201 |
230 |
250 |
240 |
220 |
240 |
Построим функцию потребления, используя модель Кейнса
формирования доходов (3).
Непосредственное оценивание структурного уравнения функции потребления обычным МНК приводит к следующим результатам:
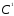 =
60,9 + 0,635Y,
=
60,9 + 0,635Y,
т.е. оценки
 =
60,9,
=
60,9,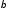 =
0,635.
=
0,635.
Было показано, что исходная модель (3) точно идентифицируема, поэтому для оценки ее структурных коэффициентов используем КМНК.
Оценка для Св приведенной форме
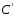 =
188 + 0,695I,
=
188 + 0,695I,
т.е.
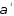 =188,
=188,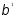 =
0,695.
=
0,695.
Из выражения (7) получим оценки структурных коэффициентов:
 =
188/(1 +0,695) = 110,9,
=
188/(1 +0,695) = 110,9,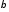 =
0,695/(1 + 0,695) = 0,41,
=
0,695/(1 + 0,695) = 0,41,
т.е.
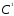 =
110,9 + 0,41Y.
=
110,9 + 0,41Y.
Оценки структурных коэффициентов функции потребления,
полученные КМНК, являются несмещенными и состоятельными.