3.9 Гетероскедастичность случайных остатков

Постоянство дисперсии случайных остатков называют гомоскедастичностъю случайных остатков. Напротив, если эта дисперсия не постоянна, то такое явление называют гетероскедастичностъю случайных остатков.

Проверка выполнения требования гомоскедастичности случайных остатков может быть произведена визуально, на основе графика остатков, или с помощью специальных критериев.

Для проведения визуального анализа необходимо построить график зависимости величин случайных остатков от выровненного значения результирующей переменной. В случае гомоскедастичности «облако» случайных остатков находится в области, параллельной оси абсцисс. Все прочие случаи соответствуют гетероскедастичности случайных остатков. Аналогичные графики можно построить также для зависимости случайных остатков от значений конкретных независимых переменных, входящих в регрессию.

К тестам, позволяющим выявить наличие гетероскедастичности случайных остатков, относят тесты Гольдфельда — Квандта, Парка, Глейзера, Уайта, Бреуша — Пагана, ранговой корреляции Спирмена и т.д.

Тест Гольдфельда—Квандта применяется, если случайные остатки предполагаются нормально распределенными величинами и объем наблюдений достаточно большой. Процедура проверки следующая.

1. Все наблюдения упорядочивают по мере возрастания ка кой-либо независимой переменной, которая, как предполагается, оказывает влияние на изменение дисперсии случайных остатков.

2. Упорядоченную совокупность делят на три группы, причем первая и последняя должны быть равного объема, с числом наблюдений, больших, чем число параметров модели регрессии. Пусть в первую и третью группы отобрано по kнаблюдений.

3. По первой и третьей группам находят параметры уравнений регрессии той же структуры, что и исходное уравнение регрессии, и остаточные суммы квадратов по каждой модели.

4. Используя данные об остаточных суммах квадратов моделей первой и третьей групп, рассчитывают фактическое значение F-критерия Фишера по формуле

(3.59)

5. Сравнивают расчётное значение F-критерия с критическим, найденным длястепеней свободы (Fкр=2,48). Общий объем наблюдений составляет 48 регионов, т.е. их можно разделить на три равные группы по 16 наблюдений в каждой или по 18 наблюдений в первой и третьей группах и 12 наблюдений во второй. Так как критерий Гольдфельда — Квандта предполагает построение уравнений регрессии той же структуры, что и исходное уравнение, остановимся на втором варианте деления совокупности как обеспечивающим боль­шую достоверность регрессионного анализа (18 наблюдений на три коэффициента регрессии, т.е. по шесть наблюдений на каждый коэффициент).

Для рассматриваемого примера Fр1=0,18;Fр2=0,13;Fр3=18,58 соответственно для независимых переменныхX1,X2иX3). Так какF- расчётное больше критического, то гипотеза об отсутствии гетероскедастичности отклоняется.

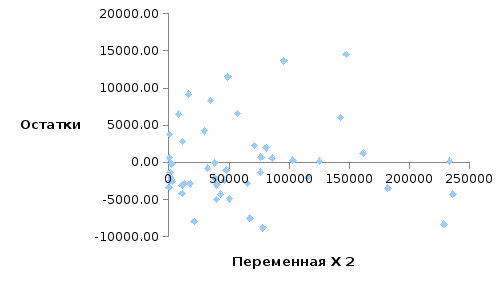
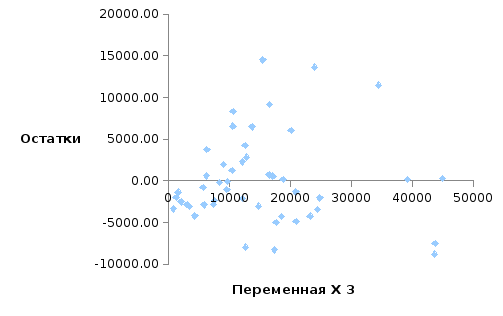
Причинами гетероскедастичности случайных остатков мо­гут быть неверная функциональная форма уравнения регрес­сии (неверная спецификация модели), неоднородность иссле­дуемой совокупности. Соответственно способами устранения гетероскедастичности являются построение модели иной фун­кциональной формы и (или) разбиение совокупности на одно­родные группы. Если по каким-то причинам это сделать не­возможно или нежелательно, то для нахождения параметров уравнения регрессии можно воспользоваться обобщенным методом наименьших квадратов.