
- •Раздел I. Статика
- •Глава 1. Основные понятия и аксиомы статики
- •Введение: предмет, метод, место среди естественных наук и границы применимости теоретической механики
- •1.2 Сила, система сил, эквивалентная система сил и уравновешенная система сил
- •1.3 Аксиомы статики и некоторые следствия из них
- •1.4 Исследование связей и установление направления их реакций
- •Глава 2. Приведение пространственной и плоской систем сходящихся сил к равнодействующей
- •2.1 Геометрический метод определения равнодействующей
- •Пространственной и плоской систем сходящихся сил
- •2.2 Условие равновесия пространственной и плоской систем сходящихся сил в геометрической форме
- •2.3 Разложение силы на сходящиеся составляющие
- •2.4 Проекции силы на ось и на плоскость
- •2.5 Определение силы по ее проекциям на координатные оси
- •2.6 Аналитический метод определения равнодействующей пространственной и плоской систем сходящихся сил
- •2.7 Условия равновесия пространственной и плоской систем сходящихся сил в аналитической форме. Указания к решению задач
- •2.8. Момент силы относительно точки. Теорема Вариньона о моменте равнодействующей
- •Глава 3. Система параллельных сил и теория пар, как угодно расположенных в одной плоскости
- •3.1 Приведение систем двух параллельных сил, направленных
- •В одну сторону, к равнодействующей
- •3.2 Приведение системы двух неравных по модулю параллельных сил, направленных в противоположные стороны, к равнодействующей
- •3.3 Пара сил. Момент пары сил
- •3.4 Эквивалентность пар
- •3.5 Сложение пар, расположенных в одной плоскости. Условие равновесия пар
- •Глава 4. Произвольная плоская система сил
- •4.1 Теорема о параллельном переносе силы. (Метод Пуансо)
- •4.2. Приведение произвольной плоской системы сил к одной силе и к одной паре
- •4.3 Приведение произвольной плоской системы сил к равнодействующей
- •4.4 Теорема Вариньона о моменте равнодействующей произвольной плоской системы сил. Условие равновесия рычага
- •4.5 Приведение произвольной плоской системы сил к одной паре
- •4.6 Условия равновесия произвольной плоской системы сил
- •4.7 Условия равновесия плоской системы параллельных сил
- •4.8 Указания к решению задач
- •4.9 Равновесие сочлененной системы тел
- •Глава 5. Трение скольжения и качения
- •5.1 Трение скольжения
- •5.2 Трение качения
- •5.3 Понятие о ферме
- •5.4 Способ вырезания узлов
- •5.5. Способ разрезов фермы
- •Глава 6. Произвольная пространственная система сил и теория пар, как угодно расположенных в пространстве
- •6.1 Момент силы относительно точки как вектор
- •6.2 Момент силы относительно оси
- •6.3. Зависимость между моментом силы относительно оси и моментом силы относительно точки, лежащей на этой оси
- •6.4 Аналитическое выражение моментов силы относительно координатных осей
- •6.5 Теорема о переносе пары в другую плоскость, параллельную плоскости действия этой пары
- •6.6 Момент пары как вектор
- •6.7 Условие эквивалентности двух пар
- •6.8 Сложение пар, лежащих в разных плоскостях. Условие равновесия пар
- •6.9 Приведение произвольной пространственной системы сил к одной силе и к одной паре
- •6.10 Изменение главного вектора-момента при перемене центра приведения
- •6.11 Инварианты произвольной пространственной системы сил
- •6.12 Приведение произвольной пространственной системы сил к динамическому винту
- •6.13 Случай приведения системы сил, не лежащих в одной плоскости, к равнодействующей. Теорема Вариньона о моменте равнодействующей
- •6.14 Случай приведения системы сил, не лежащих в одной плоскости, к паре
- •6.15 Условия равновесия произвольной пространственной системы сил. Случай пространственной системы параллельных сил
- •6.16 Равновесие твердого тела с одной и с двумя закрепленными точками. Указания к решению задач
- •Глава 7. Центр тяжести
- •7.1 Приведение системы параллельных сил к равнодействующей. Центр параллельных сил
- •7.2 Центр тяжести
- •7.3 Способы определения координат центров тяжести тел
- •7.4 Центр тяжести некоторых линий, площадей и объемов
- •7.5 Графическое определение положения центра тяжести плоских фигур
Глава 7. Центр тяжести
7.1 Приведение системы параллельных сил к равнодействующей. Центр параллельных сил
Если на тело
действует пространственная система
параллельных и в разные стороны
направленных сил
![]() ,
,
![]() ,
...,
,
...,
![]() (рисунок 114), то, выбрав координатные оси
так, чтобы ось z
была параллельна заданным силам, а
плоскость хОу
к ним перпендикулярна, по формулам (5,
8, §39) будем иметь
(рисунок 114), то, выбрав координатные оси
так, чтобы ось z
была параллельна заданным силам, а
плоскость хОу
к ним перпендикулярна, по формулам (5,
8, §39) будем иметь
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
По формулам (6, 9,
§6.9) найдем модуль главного вектора
![]() и главного вектора-момента
и главного вектора-момента
![]() .
При этом из формул (7, 10, §39) следует, что
главный вектор
.
При этом из формул (7, 10, §39) следует, что
главный вектор
![]() при выбранном центре приведения в точке
О
расположен на оси z,
а главный вектор-момент
при выбранном центре приведения в точке
О
расположен на оси z,
а главный вектор-момент
![]() – в плоскости
хОу
(рисунок 114). Следовательно, главный
вектор
– в плоскости
хОу
(рисунок 114). Следовательно, главный
вектор
![]() перпендикулярен к главному вектору-моменту
перпендикулярен к главному вектору-моменту
![]() ,
а поэтому пространственная
система параллельных сил никогда не
приводится к динаме.
Она приводится к равнодействующей, если
,
а поэтому пространственная
система параллельных сил никогда не
приводится к динаме.
Она приводится к равнодействующей, если
![]() ,
или к паре, если
,
или к паре, если
![]() ,
или взаимно уравновешивается, если
,
или взаимно уравновешивается, если
![]() и
и
![]() .
.
Рассмотрим теперь
пространственную систему параллельных
и одинаково направленных сил
![]() ,
,
![]() ,
...,
,
...,
![]() (рисунок 115), приложенных к телу в точках
(рисунок 115), приложенных к телу в точках
![]() ,
,
![]() ,
…,
,
…,
![]() .
Очевидно, что эта система сил приводится
к равнодействующей. Найдем эту
равнодействующую.
.
Очевидно, что эта система сил приводится
к равнодействующей. Найдем эту
равнодействующую.
Рассмотрим сначала
силы
![]() и
и
![]() .
В главе III, §12, было показано, что
равнодействующая
.
В главе III, §12, было показано, что
равнодействующая
![]() сил
сил
![]() и
и
![]() по модулю равна
по модулю равна
![]() ,
им параллельна и направлена в ту же
сторону. При этом линия действии
равнодействующей
,
им параллельна и направлена в ту же
сторону. При этом линия действии
равнодействующей
![]() ,
проходит через точку
,
проходит через точку
![]() ,
которая лежит на отрезке
,
которая лежит на отрезке
![]() соединяющем точки приложения составляющих
сил
соединяющем точки приложения составляющих
сил
![]() и
и
![]() ,
и делит этот отрезок на части, обратно
пропорциональные составляющим силам:
,
и делит этот отрезок на части, обратно
пропорциональные составляющим силам:
![]() . (1)
. (1)
И з
этого соотношения следует, что положение
точки
з
этого соотношения следует, что положение
точки
![]() зависит только от модулей составляющих
сил и расположения их точек приложения
и не зависит от направления этих сил.
Если силы
зависит только от модулей составляющих
сил и расположения их точек приложения
и не зависит от направления этих сил.
Если силы
![]() и
и
![]() повернуть около их точек приложения
повернуть около их точек приложения
![]() и
и
![]() на один и тот же угол в одну и ту же
сторону, то точка
на один и тот же угол в одну и ту же
сторону, то точка
![]() сохранит свое положение, и равнодействующая
сохранит свое положение, и равнодействующая
![]() повернется вокруг нее на этот же угол.
повернется вокруг нее на этот же угол.
Рассмотрим теперь
силы
![]() и
и
![]() .
Равнодействующая
.
Равнодействующая
![]() этих сил по модулю равна
этих сил по модулю равна
![]() ,
им параллельна, направлена в ту же
сторону и проходит через точку
,
им параллельна, направлена в ту же
сторону и проходит через точку
![]() .
При этом точка
.
При этом точка
![]() обладает таким же свойством, каким и
точка
обладает таким же свойством, каким и
точка
![]() .
.
Применив это
рассуждение для равнодействующей
![]() и силы
и силы
![]() и т. д., придем к заключению, что
равнодействующая
и т. д., придем к заключению, что
равнодействующая
![]() пространственной системы параллельных
сил
пространственной системы параллельных
сил
![]() ,
,
![]() ,
...,
,
...,
![]() ,
направленных в одну сторону, равна по
модулю сумме модулей этих сил, им
параллельна и направлена в ту же сторону.
При этом линия действия равнодействующей
проходит через одну и ту же точку С,
положение которой по отношению к точкам
,
направленных в одну сторону, равна по
модулю сумме модулей этих сил, им
параллельна и направлена в ту же сторону.
При этом линия действия равнодействующей
проходит через одну и ту же точку С,
положение которой по отношению к точкам
![]() ,
,
![]() ,
…,
,
…,
![]() ,
т. е. к телу, будет неизменным.
,
т. е. к телу, будет неизменным.
Точка С, через которую проходит равнодействующая системы параллельных сил при любых поворотах этих сил около их точек приложения в одну и ту же сторону и на один и тот же угол, называется центром параллельных сил.
Найдем теперь
координаты центра параллельных сил.
Положение точки С
по отношению к телу является неизменным
и от выбора системы осей координат Охуz
не зависит. Найдем сначала положение
центра двух параллельных сил
![]() и
и
![]() (рисунок 116).
(рисунок 116).
Пусть радиус-вектор
![]() определяет положение точки приложения
силы
определяет положение точки приложения
силы
![]() ,
а радиус-вектор
,
а радиус-вектор
![]() ,
– точки приложения силы
,
– точки приложения силы
![]() .
Линия действия равнодействующей
.
Линия действия равнодействующей
![]() этих сил пересекает отрезок
этих сил пересекает отрезок
![]() в точке
в точке
![]() .
Изменим направление сил
.
Изменим направление сил
![]() и
и
![]() ,
повернув их на некоторый произвольный
угол
,
повернув их на некоторый произвольный
угол
![]() .
При этом линия действия новой
равнодействующей
.
При этом линия действия новой
равнодействующей
![]() будет пересекать отрезок
будет пересекать отрезок
![]() ,
также в точке
,
также в точке
![]() .
Следовательно, по определению, точка
.
Следовательно, по определению, точка
![]() представляет собой центр параллельных
сил
представляет собой центр параллельных
сил
![]() и
и
![]() .
Предположим, что радиус-вектор,
определяющий положение точки
.
Предположим, что радиус-вектор,
определяющий положение точки
![]() ,
есть
,
есть
![]() .
Очевидно (рисунок 116), что
.
Очевидно (рисунок 116), что

![]() и
и
![]() .
.
Так как векторы
![]() и
и![]() (рисунок 116) коллинеарны, то соотношение
(1) можно записать в виде
(рисунок 116) коллинеарны, то соотношение
(1) можно записать в виде
 ,
или
,
или
 . (2)
. (2)
Разрешая равенство
(2) относительно
![]() ,
получаем
,
получаем
 . (3)
. (3)
Эта формула
определяет положение центра
![]() двух параллельных сил
двух параллельных сил
![]() и
и
![]() .
.
Для определения
радиуса-вектора
![]() ,
определяющего положение центра трех
параллельных сил:
,
определяющего положение центра трех
параллельных сил:![]() ,
,![]() и
и![]() ,
можно воспользоваться формулой (3) и
определить по ней положение центра двух
параллельных сил:
,
можно воспользоваться формулой (3) и
определить по ней положение центра двух
параллельных сил:![]() и
и
![]() .
Пусть положение точки приложения силы
.
Пусть положение точки приложения силы![]() ,
определяется радиусом-вектором
,
определяется радиусом-вектором![]() .
Тогда положение центра
.
Тогда положение центра![]() трех параллельных сил:
трех параллельных сил:![]() ,
,![]() и
и![]() – будет согласно формуле (3) определяться
так:
– будет согласно формуле (3) определяться
так:
 . (4)
. (4)
Аналогичным приемом
мы получим и радиус-вектор
![]() ,
определяющий положение центраС
системы n
параллельных сил:
,
определяющий положение центраС
системы n
параллельных сил:
 ,
или
,
или
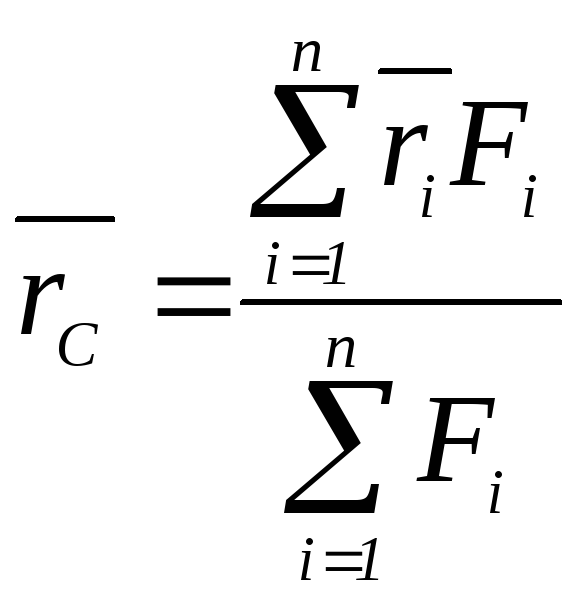 , (5)
или
, (5)
или
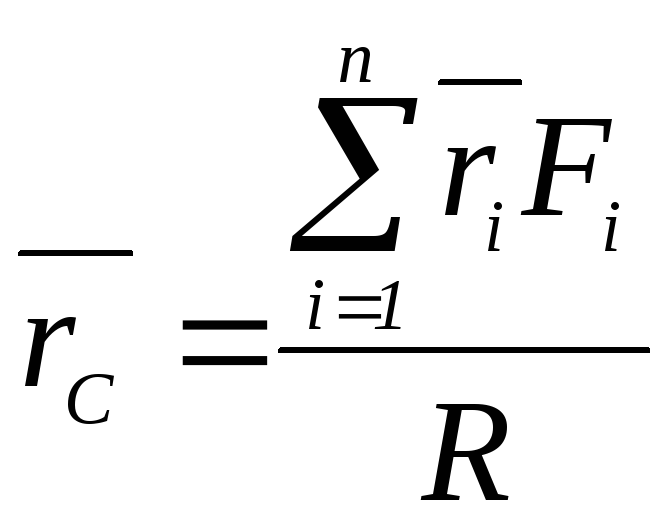 , (6)
где
, (6)
где
![]() модуль равнодействующей
модуль равнодействующей![]() пространственной системы параллельных
сил
пространственной системы параллельных
сил![]() ,
,![]() ,
…,
,
…,![]() ,
,![]() – радиус-вектор точки приложения
– радиус-вектор точки приложения![]() силы
силы![]() .
.
Проектируя векторное равенство (6) на оси координат, получим координаты центра параллельных сил в виде
 ;
;
 ;
;
 . (7)
. (7)
Заметим, что формулы
(6) и (7) будут справедливы и для параллельных
сил, направленных в разные стороны, если
в них считать
![]() величинами алгебраическими (для одного
направления со знаком "плюс", для
другого – "минус") и если при этом
величинами алгебраическими (для одного
направления со знаком "плюс", для
другого – "минус") и если при этом![]()
Применим теперь формулы (6) и (7) к определению положения центра тяжести тел.
