Лабораторные работы 5 симестр / Радиоизмерения / ri13

Лабораторная работа № 7 Гармонический анализ

Введение

Цель работы: изучение спектров различных радиосигналов.

Любое радиоэлектронное устройство реагирует на радиосигнал как на совокупность простых гармонических (синусоидальных) сигналов различной частоты. Для выявления этой совокупности применяется гармонический анализ, использующий разложение в ряды Фурье (для периодических сигналов) и преобразование Фурье (для непериодических сигналов).

В радиоэлектронных устройствах действуют сигналы различной формы. Они могут быть периодическими и непериодическими. Функция называется периодической, если существует такое число Т, называемое периодом, что выполняется условие:

, (1)

Строго говоря, функция должна существовать бесконечно долго. Кроме сигналов, имеющих форму гармонической функции, то есть вида:

, (2)

Широкое распространение в радиотехнике получили и негармонические (сложные) сигналы. Например, такие как амплитудно-модулированный сигнал, рис.1а, колебания типа «меандр», рис.1, б, импульсы, рис.1, в.

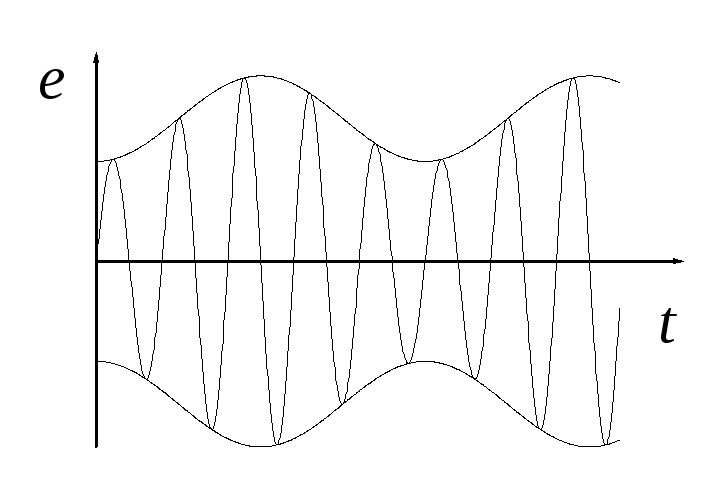
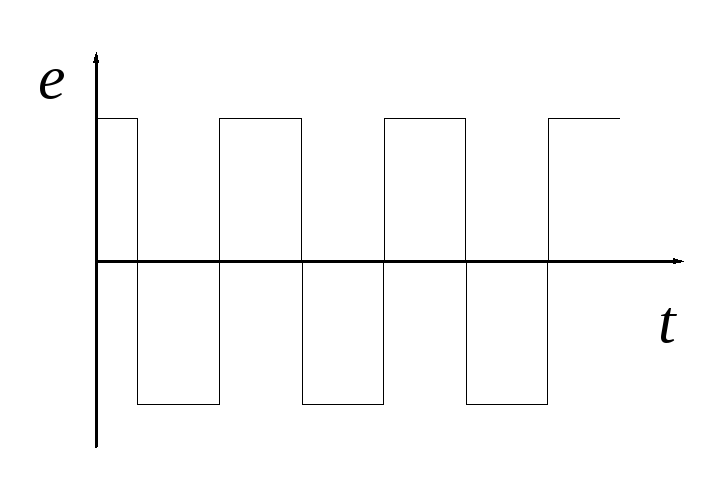
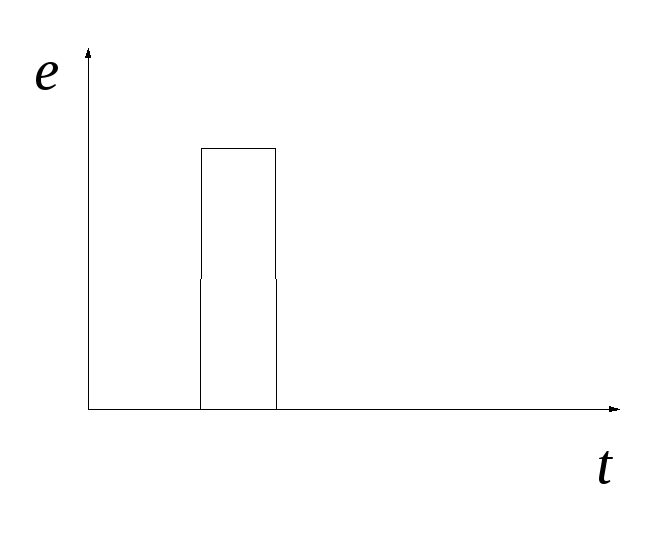
а) б) в)

Рис. 1

В современной радиотехнике нашел широкое применение спектральный метод анализа действия сложных ЭДС на различные цепи.

При этом сложные ЭДС представляются через простые – гармонические составляющие. Совокупность гармонических составляющих сложной ЭДС называется спектром этого сигнала. Спектр может быть представлен в виде графика, изображающего зависимость амплитуд гармонических составляющих от частоты.

1. Спектр периодических ЭДС. Ряд Фурье

Если периодическая функция удовлетворяет условиям Дирихле, то ее можно представить рядом тригонометрических функций, то есть рядом Фурье

, (3)

где

, (4)

— среднее значение функции за период (постоянная составляющая).

, (5)

– коэффициент разложения для косинусоидальных составляющих ряда Фурье.

, (6)

– коэффициент разложения для синусоидальных сигналов.

Если функция четная, то , если функция нечетная, то . Формулу (3) можно записать в другой форме:

, (7)

Здесь

, (8)

– угловая частота первой гармоники, то есть колебания, период которых равен периоду разлагаемой функции

, (9)

, (10)

, (11)

, (12)

где – амплитуда -той гармоники, – начальная фаза -той гармоники.

Используя формулу Эйлера

, (13)

ряд Фурье (7) можно записать в комплексной форме

В качестве примера найдем спектр сигнала, имеющего форму периодических импульсов (рис.2).

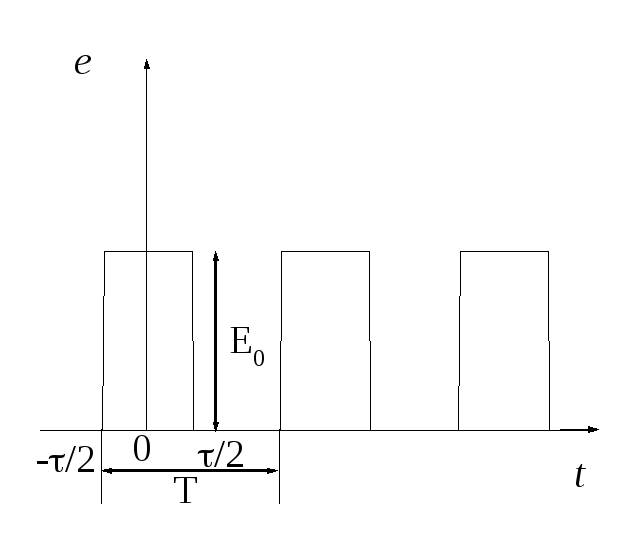
Рис. 2

Начало отсчета мы выбираем таким образом для того, чтобы функция получилась четной

,

где – постоянная составляющая сигнала.

Так как 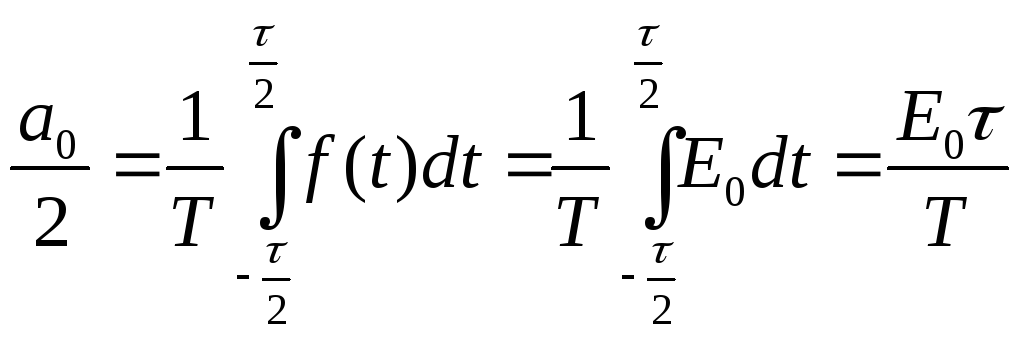, то

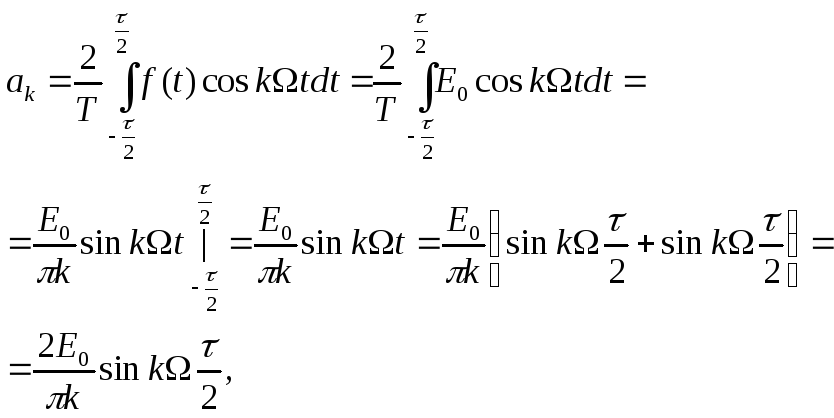
Если мы пользуемся комплексной формой ряда Фурье, нам необходимо найти комплексную амплитуду или спектральную функцию

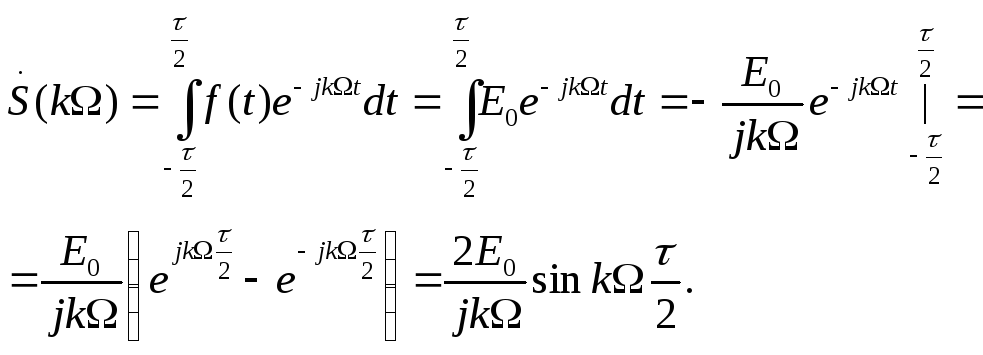
Рис. 3.	Рис. 4.

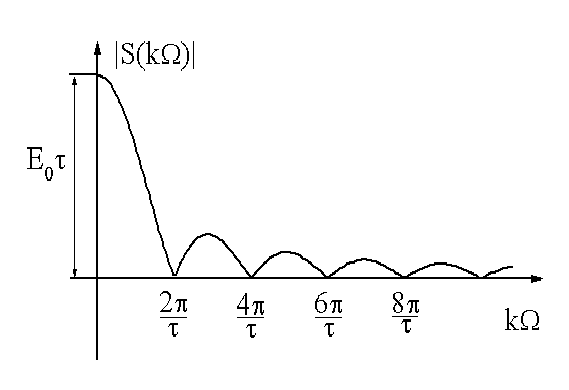
График спектральной функции представлен на рис.3, а модуль спектральной функции на рис.4.

Частотный спектр последовательности импульсов можно графически представить следующим образом (рис.5).

Следует отметить, что спектральная функция не зависит от периода Т.

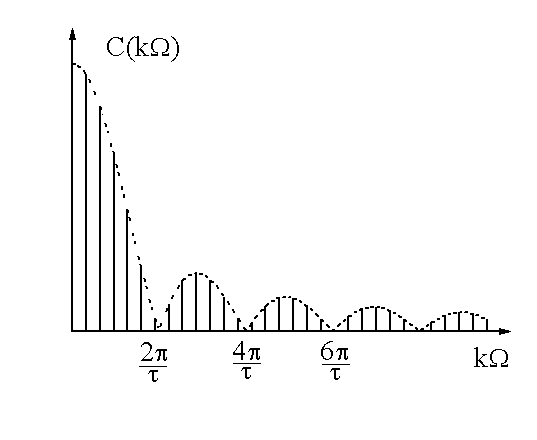
Рис. 5.

2. Спектр непериодической ЭДС. Интеграл Фурье.

Непериодический сигнал (рис.6) можно представить как периодический с . При увеличении периода следования до бесконечности величина стремится стать бесконечно малой. Это означает, что интервалы между линиями спектра по шкале частот (рис.5) становятся бесконечно малыми – . Так как дискретные значения частот теряют смысл, вместо частоты целесообразно использовать понятие текущей частоты .

Выполнение работы

1. Ознакомится с описанием генератора сигналов специальной формы и анализатора спектра.

2. Для предложенных преподавателем сигналов генератора получить осциллограмму и записать величины первых 4-5 спектральных составляющих.

3. На одном графике изобразить осциллограмму сигнала и этот же сигнал, восстановленный как: а) сумма 1 и 2 гармоник; б) сумма 1, 2 и 3 гармоник.

4