2. Волна типа

Рассмотрим этот тип колебаний в прямоугольном волноводе более подробно как из-за большей наглядности, так и из-за широкого практического использования этого типа колебаний.

Начнем с построения качественной картины поля. При этом в качестве исходной можно использовать структуру поля волны в волноводе, образованиом двумя идеально проводящими плоскостями.

20. −Построение картины распределения электромагнитного поля типа

Обращаясь к рисунку Рисунок 20 , заметим, что поскольку силовые линии электрического вектора здесь параллельны поперечной координате , во внутреннем пространстве волновода можно установить две идеально проводяшие перегородки. отстоящие друг от друга на расстояние. В силу перпендикулярности векторов поляЕк этим перегородкам граничные условия на последних будут выполняться автоматически. Таким образом, можно рассматривать лишь поля, существующие в замкнутой области с прямоугольной формой сечения, то есть перейти к прямоугольному волноводу.

Чрезвычайно важно отметить, что данная картина поля останется справедливой при любом расстоянии между перегородками или, согласно принятой здесь терминологии, при любом размере узкой стенки волновода. Отсюда следует, что величинане должна входить в выражение, определяющее критическую длину волны для данного типа колебаний. Действительно, при,будем иметь

.

Поскольку волна типа в рассматриваемом волноводе является низшим типом колебаний, можно сформулировать полученный результат следующим образом: по прямоугольному волноводу могут передаваться лишь колебания с длинами волн, меньшими, чем удвоенный размер широкой стенки; более длинноволновые колебания по волноводу принципиально распространяться не могут.

Передачу электромагнитной энергии от генератора к нагрузке по волноводу следует вести на основном типе колебаний, так как анализ показывает, что при этом потери энергии в волноводе минимальны. Для того, чтобы в волноводе имели место только колебания типа, необходимо выбрать рабочую длину волныменее, но более,,и других критических длин волн. Практически необходимо соблюдать условие

Запишем сводку аналитических выражений для составляющих электромагнитного поля волны :

,

где 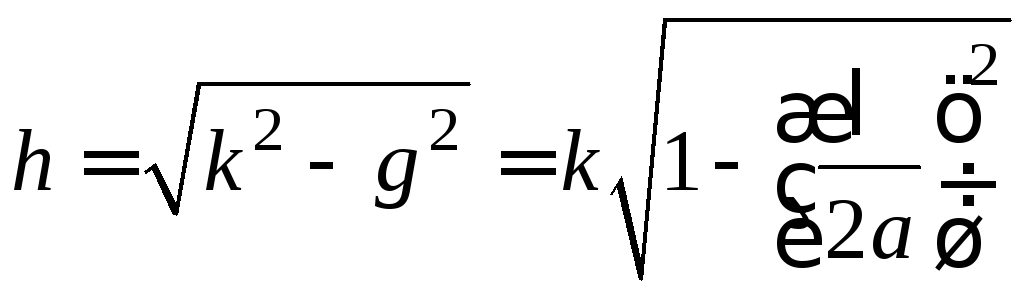− продольное волновое число,− постоянная распространения (волновое число) в свободном пространстве..

Данные формулы получены с помощью правил перехода от продольных компонет к поперечным. Как видно, в векторах поля волны типа присутствуют всего три составляющие. Рассмотрим их распределение внутри волновода подробнее.

Воспользовавшись методом комплексных амплитуд, определим мгновенные значения каждой компоненты в зависимости от времени. Для этого нужно будет заменить наи умножить комплексные амплитуды на временной экспоненциальный множитель. Взяв затем от полученных формул действительную часть по формуле Эйлера, получим

.

Остальные компоненты поля равны нулю. Построим теперь точное распределение силовых линий для момента времени . Из выражений следует, что напряженность электрического поля имеет лишь одну составляющую, паралелльную оси. При этом величина составляющей не зависит от координаты. Поэтому электрические силовые линии представляют собой прямые, параллельные узкой стенке волновода (рисунок Рисунок 21 ). Напряженность электрического поля в любом поперечном сечении волновода, параллельном плоскости, зависит лишь от координатыи меняется в соответствии с зависимостью. Наибольшее значение напряженность принимает при, т.е. в середине широкой стенки волновода. Следовательно, зависимость напряженности поля от координатыхарактеризуется полусинусоидой.

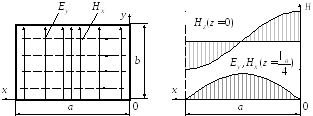
21. −Распределение поля в поперечном сечении волновода

В направлении оси величинапри фиксированном времени изменяется по закону синуса и прив плоскостинапряженность. Поэтому на рисунке Рисунок 21 построено распределениев плоскостипри, когдаимеет максимальное значение, направленное сверху вниз. В середине силовые линии располагаются густо, указывая на максимум напряженности поля, и становятся более редкими по направлению к краям. Через половину периода времени направление силовых линий становится обратным.

Величина составляющей напряженности магнитного поля изменяется по координатам, как это следует из выражений для поля, аналогично изменению величины напряженности электрического поля.

Величина же составляющей по координатеизменяется по закону косинуса, т.е.имеет максимальные противоположные по знаку значения у вертикальных (узких) стенок волновода,, и нулевое значение на середине поперечного сечения волновода.

В направлении распространения электромагнитных колебаний, т.е., в направлении оси , составляющаяопределяется также законом косинуса:. Поэтому эта составляющая сдвинута относительноиво времени на четверть периода, а в направлении распСААространения (оси) −на четверть длины волны, т.е., приив точкевеличинамаксимальна, а в точкеона равна нулю.

Напряженность магнитного поля имеет только составляющие и, т.е., силовые линии магнитного поля представляют собой замкнутые линии, параллельные плоскости. На рисунке Рисунок 22 представлена картина поля волныв волноводе при,. Как и везде на наших рисунках, силовые линии векторапоказаны сплошными линиями, а вектора−пунктирными. На рисунке Рисунок 22 , а) − силовые линии в среднем продольном вертикальном сечении волновода, т.е., вид со стороны узкой стенки; на рисунке Рисунок 22 , б) − распределение напряженности электрического поляи составляющеймагнитного поля вдоль продольной оси волновода, на рисунке Рисунок 22 , в) − силовые линии магнитного поля в горизонтальном сечении волновода (вид со стороны широкой стенки).

Таким образом, для волны типа значения индексовипоказывают, что в направлении осираспределению амплитуд составляющих напряженности поля соответствует одна полуволна, а в направлении осиполе однородно. Вся совокупность силовых линий движется вдоль осис фазовой скоростью.

а)

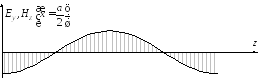
б)

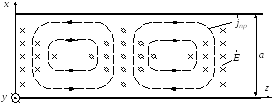
в)

22. −Распределение поля вдоль волновода

(в данной лекции присутствовала демонстрация моделирования распространения плоских волн в разных средах и моделирование поля разных типов волн в прямоугольном волноводе)