4. Вычисление критической длины волны и длины волны в волноводе

Основываясь на приведенном здесь анализе волн типа Е, найдем связь между продольным волновым числом, двумя геометрическими параметрами волновода — размерами сеченияии длиной волны возбуждающего генератора.

На основании материала, рассмотренного выше, имеем

.

Напомним, что входящие в это уравнение постоянная распространения в свободном пространстве и продольное волновое числоочень просто связаны с длиной волны генератораи длиной волны в волноводе:

,.

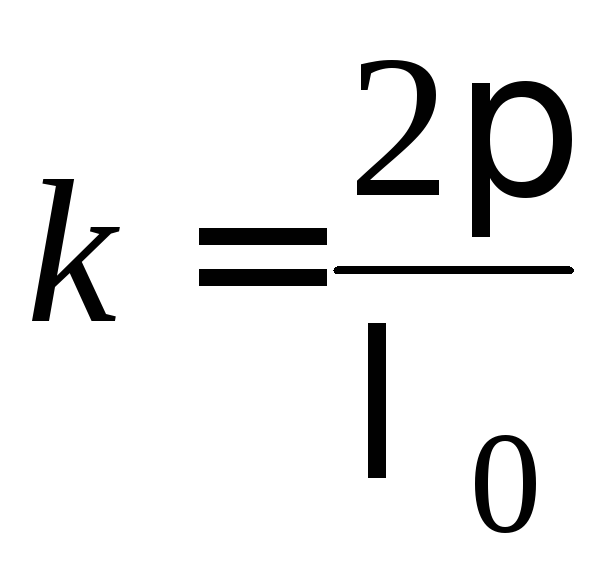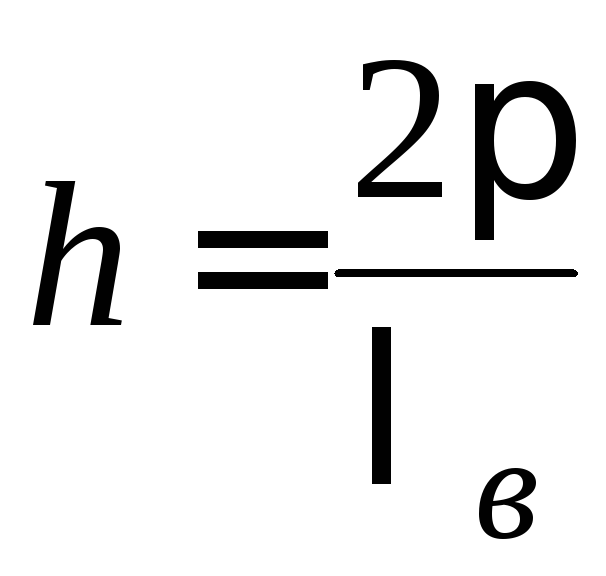В свою очередь, поперечное волновое число , определяемое формулой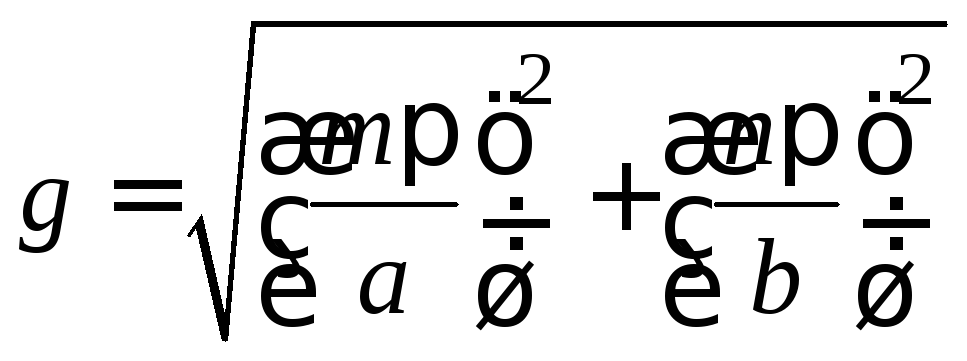, зависит лишь от геометрических размеров сечения и от индексов выбранного типа волны и совершенно не зависит от частоты.

Выражение для поперечного волнового числа позволяет вскрыть важнейшую особенность работы любого волновода рассматриваемого типа. Если , то продольное волновое число является вещественным, а это, как уже известно, означает распространение данного колебания в виде бегущих волн. Ести длина волны генератора увеличена настолько, что, то вместо бегущей волны в волноводе существуют нераспространяющиеся колебания, амплитуда которых экспоненциально уменьшается по координате. Об этом свидетельствует мнимый характер продольного волнового числа.

Граничный случай возникает, когда равно. При этоми, как следствие,. Принято говорить, что в данных условиях рассматриваемый тип колебаний находится в критическом режиме. Значение длины волны генератора, соответствующее случаю, называется критической длиной волны для данного типа колебаний в исследуемом волноводе и обозначается. Во избежание недоразумений в ряде случаев приходится указывать, к какому типу колебаний эта величина относится, или, по крайней мере, обозначать индексы рассматриваемого типа колебаний.

Из приведенных рассуждений следует, что 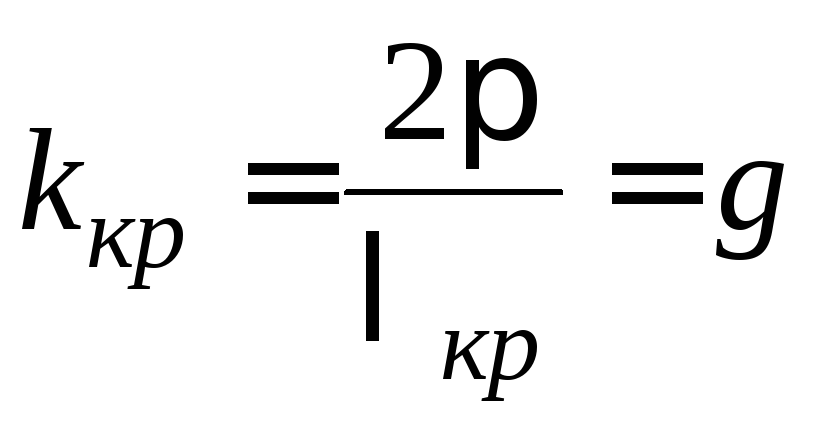, откуда

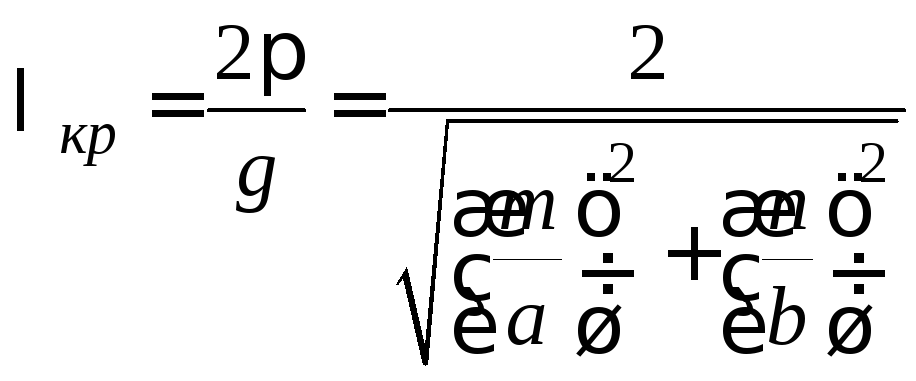
Связь между тремя волновыми числами ,иможет быть вььражена через соответствующие длины волн следующим образом:

.

Это равенство показывает, что при изменении величины генератора длина волны в волноводе изменяется не пропорционально ей. Закон зависимости длины волны в волноводе от длины волны в свободном пространстве носит название дисперсионной характеристики волновода. В явном виде эта характеристика описывается формулой, вытекающей из предыдущего соотношения

.

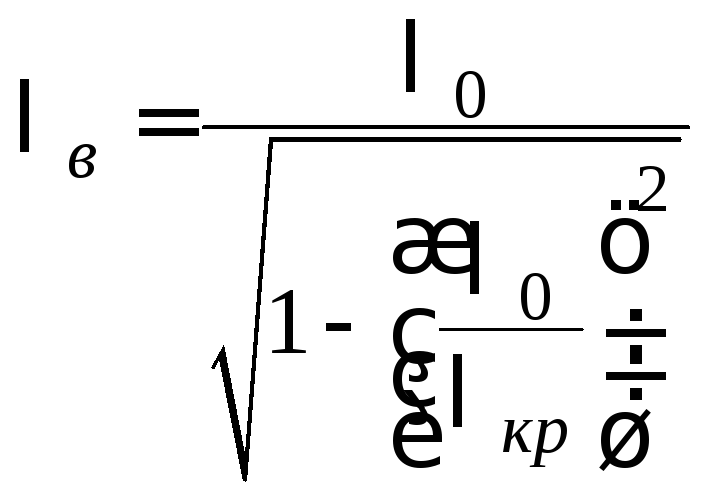Легко заметить, что вывод этой формулы основан только на двух предпосылках: пропорциональности комплексных амплитуд бегущих волн множителю и существовании понятия критической длины волны. Поскольку обе предпосылки справедливы для любого типа колебаний в полом металлическом волноводе с произвольной формой поперечного сечения, то полученный результат имеет универсальное значение для всех рассматриваемых волноводов. Разница будет обнаруживаться лишь в различных способах вычисления величины. Дисперсионную характе-ристику волновода весьма удобно изобразить на графике, подобном приведенному на рисунке Рисунок 19 .

19. −Дисперсионная характеристика волновода

Вся область длин волн, меньших, чем , является областью «прозрачности» данного волновода на рассматриваемом типе колебаний; причем, если, то длина волны в волноводе лишь в очень малой степени отличается от длины волны в свободном пространстве, всегда превосходя ее. Еслина графике рисунка Рисунок 19 стремится кслева, то длина волны в волноводе стремится к бесконечности. При переходечерез граничное значение в волноводе имеются уже не бегущие, а экспоненциально затухающие волны. Всю область частот, которой соответствуют, называют областью непрозрачности или областью отсечки.

То, что длина волны в волноводе всегда превосходит длину волны в свободном пространстве, обусловлено тем, что как волны типа Е, так и волны типаНв волноводах с идеально проводящими стенками распространяются с фазовыми скоростями, большими, чем скорость света в вакууме. Поскольку фазовая скорость, длина волны и частота связаны очевидным соотношением, из выражения для длины волны в волноводе следует формула для вычисления фазовой скорости

.
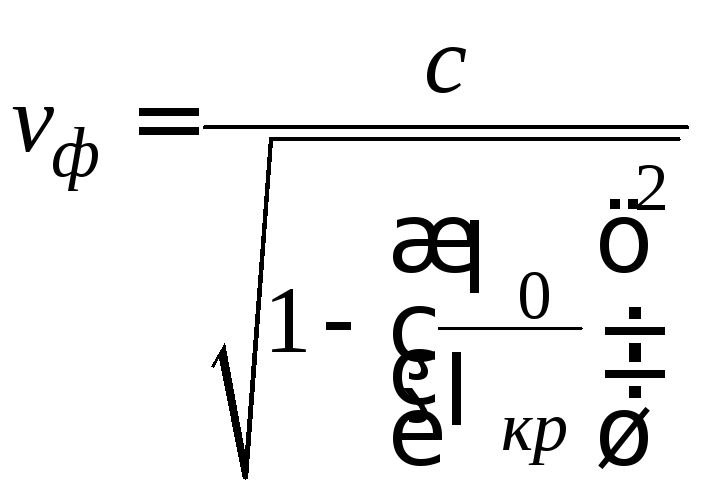