3. Падение плоской волны с перпендикулярной поляризацией

Принципиальным отличием данного случая от рассмотренного выше случая параллельной поляризации является то, что здесь в плоскости падения лежит вектор, тогда как векторпараллелелен оси. Не останавливаясь на уже изложенных деталях графического построения, приведем окончательную картину суммарного поля.

Характерной особенностью даной картины является то, что здесь суммарное электрическое поле направлено вдоль оси , т.е. поперечно по отношению к продольной оси. В то же время магнитные силовые линии образуют замкнутые петли, лежащие в плоскости. Легко показать, что при этом магнитное поле будет иметь две декартовы составляющиеи.

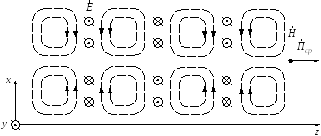
11. −Результирующая картина силовых линий поля при падении плоской волны с перпендикулярной поляризацией

4. Классификация направляемых волн

По структуре поля направляемые волны классифицируются в зависимости от наличия или отсутствия в ни продольных составляющих векторов электрического либо магнитного полей. При этом под продольным направлением подразумевается направление распространения волны. Как следует из рассмотренных выше примеров, здесь могут быть три случая.

1. Оба вектора, электрический и магнитный, перпендикулярны оси расространения и, следовательно, не имеют продольных составляющих: 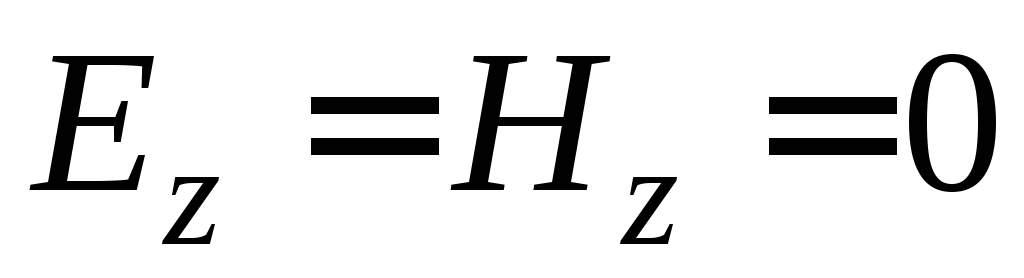. Такие волны носят название поперечных волн или волн типа ТЕМ (transverseelectromagnetic). В частности, волной типа ТЕМ является плоская волна, распространяющаяся в неограниченном пространстве.

2. Электрический вектор имеет отличную от нуля продольную составляющую 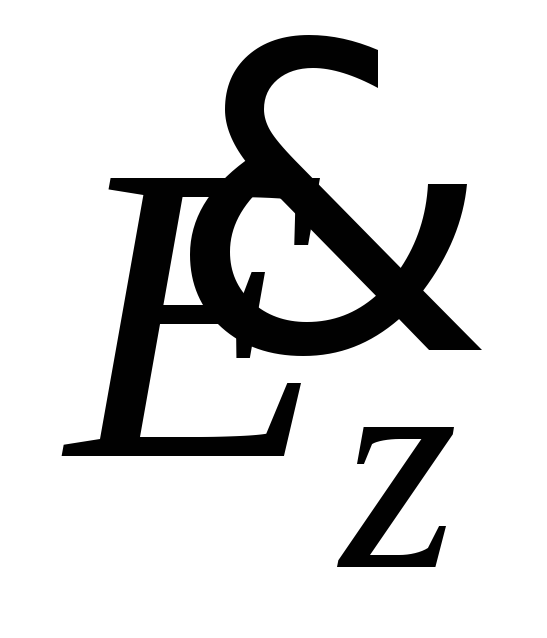, в то время как магнитное поле волны поперечно,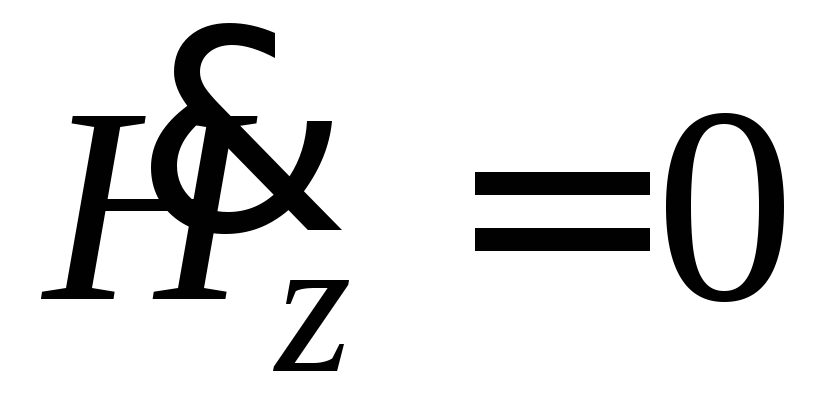. Такие направляемые волны называются волнами типа Е или ТМ волнами (transversemagnetic). Примером волны типа Е служит результирующий волновой процесс, возникающий при падении на металлическую плоскость плоской волны с параллельной поляризацией.

3. Наконец, возможен случай, когда продольную составляющую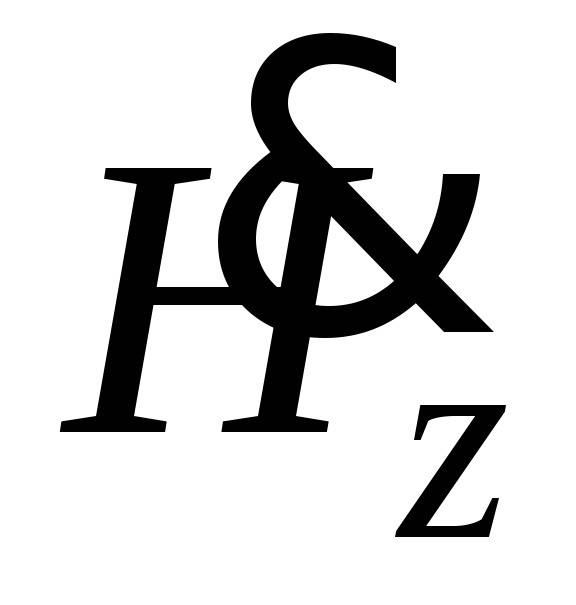имеет магнитный вектор, а электрическое поле поперечно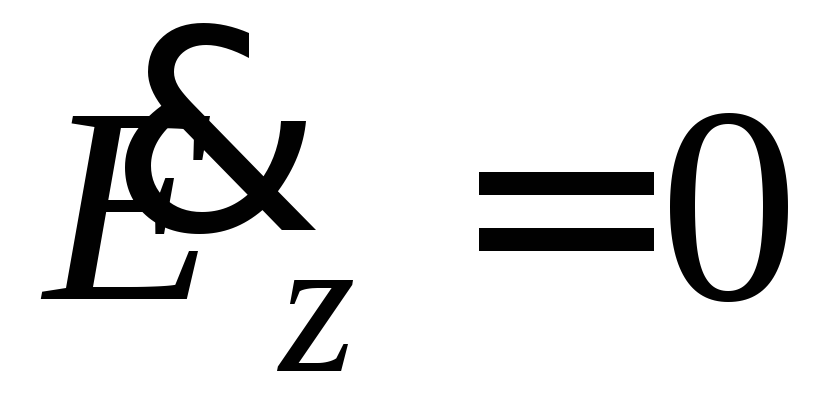. Такие волны, называемые волнами типа Н или ТЕ (transverseelectric) возникают, например, в рассмотренном выше случае, когда на проводяющую плоскость падает плоская волна с перпендикулярной поляризацией.

Существуют также смешанные, или гибридные волны, у которых оба вектора наряду с поперечными имеют и продольные составляющие. Однако, строгий анализ показывает, что подобные волны физически не могут существовать в наиболее важных для практики волноводных системах.

5. Фазовая скорость направляемых волн

Приведенные на рисунке Рисунок 10 и рисунке Рисунок 11 картины силовых линий для волн типов ЕиH, являются, по существу, мгновенными фотографиями поля, отображающими волновые процессы в какой-либо фиксирванный момент времени. Несомненно, что эти картины перемещаются в пространстве с некоторой скоростью, которую нужно вычислить.

Для определенности будем рассматривать волну типа Е, поскольку для волн типаНвыводы будут полностью аналогичными. Запишем комплексные амплитуды электрических векторов падающей и отраженной волн в следующем виде:

,

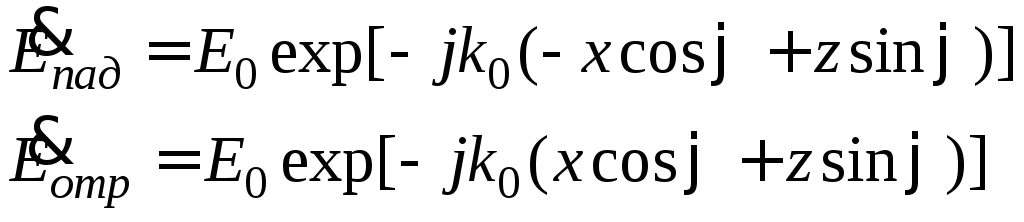где 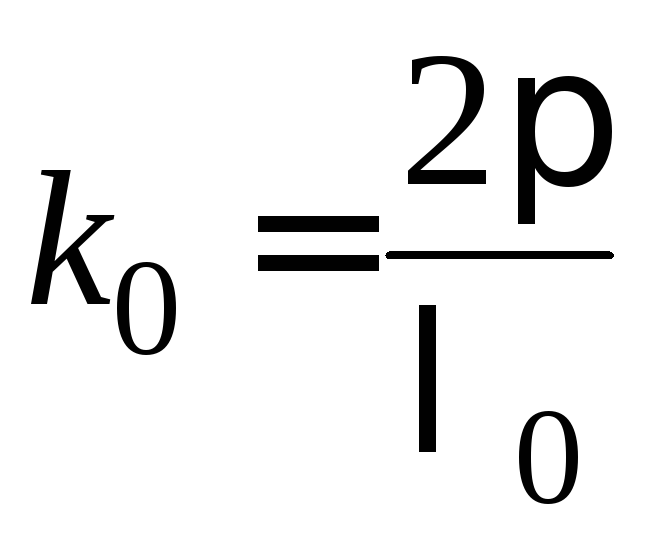− фазовая постоянная распространения, или волновое число вакуума.

Вектор суммарного поля будет обладать составляющими, равными суммам составляющих векторов и. В частности, суммарная-я составляющая оказывается равной

.

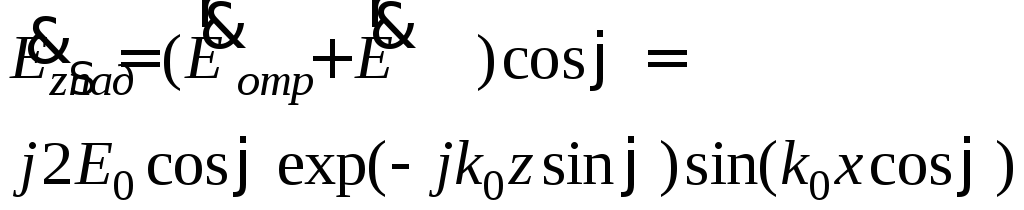Первый сомножитель в этой формуле является несущественной произвольной постоянной. Поэтому проанализируем второй и третий сомножители, описывающие зависимость составляющейот декартовых координат.

Наличие второго сомножителя показывает, что результирующее поле представляет собой волну, бегущую вдоль координаты, причем постоянная распространения зависит от угла падения. В дальнейшем будем называть эту постоянную распространения продольным волновым числом и обозначать через:

.

Наличие третьего сомножителя в формуле для суммарного поля приводит к тому, что рассматриваемый волновой процесс существенно отличается от однородной плоской волны, поскольку здесь амплитуда поля уже не постоянна в пределах волнового фронта, параллельного плоскости , а изменяется по синусоидальному закону вдоль поперечной координаты. Легко видеть, что скорость изменения амплитуды определяется «поперечной частотой»

,

которую бдуем называть поперечным волновым числом. Продольное и поперечное волновые числа связаны очевидным соотношением (рисунок Рисунок 12 )

.

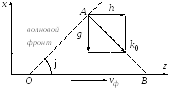
12. −Волновые числа и фазовая скорость

Физическая сущность поперечного и продольного волновых чисел остается той же, что и для полного волнового числа: они показывают расстояние, которое должна пройти волна в метрах, чтобы ее фаза изменилась на , т.е. на полный период. Для продольного волнового числа это расстояние по оси, для поперечного − по оси.

Итак, определено важное свойство направляемых волн, состоящее в следующем. Данный волновой процесс является неоднородной плоской волной, которая распространяется вдоль оси . При этом амплитуда поля изменяется вдоль поперечной координатыпо закону стоячей волны.

Вычислим скорость перемещения поверхности равных фаз (волнового фронта) вдоль координаты , т.е. фазовую скорость направляемой волны. Поскольку здесь роль постоянной распространения играет продольное волновое число, то из общего выражения для фазовой скорости будем иметь:

.

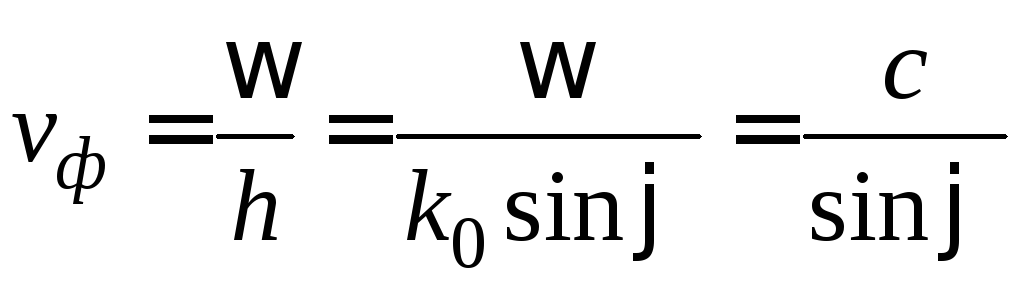Отсюда следует принципиально важный вывод: за исключением предельного случая фазовая скорость направляемых волн всегда превосходит скорость плоских электрмагнитных волн, в частности, скорость света в вакууме:. Данный вывод нуждается в обсуждении, поскольку, согласно теории относительности, скорость света в вакууме имеет предельный характер. Однако следует учитывать, что это утверждение относится лишь к движению материальных объектов. В противоположность этому фазовая скорость является скоростью перемещения в пространстве некоторой воображаемой поверхности − волнового фронта. Поэтому ограничения, накладываемые теорией относительности, в данном случае не справедливы.

Неограниченное возрастание фазовой скорости при стремлении к нулю угла падения можно проиллюстрировать следующим образом. Пусть фазовые фронты падающей волны движутся в пространстве со скоростью так, как это показано на рисунке Рисунок 12 . Можно найти скорость скорость перемещения точки пересечения фазового фронта с направляющей поверхностью. Если за единицу временифронт падающей волны проходит расстояние, то точка его пересечения с осьюдолжна пройти расстояние. Так как, то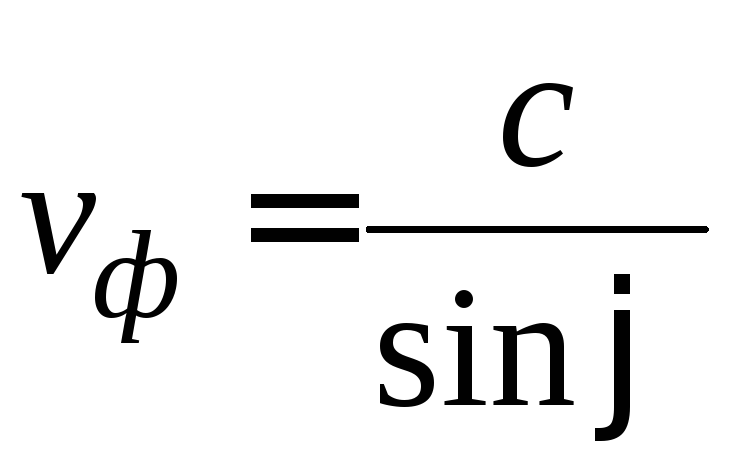, на что и указывает приведенная выше формула. В предельном случае падения волны по направлению нормали фазовая скорость вдоль осиобращается в бесконечность.