4. Элементарный электрический излучатель

Элементарным электрическим излучателем (вибратором) называется отрезок проводника, по которому протекает переменный электрический ток, причем длина проводника значительно меньше длины волны в вакууме.

С физической точки зрения по элементарному электрическому излучателю ток протекает следующим образом. В разрыв излучающего проводника включается генератор (рисунок Рисунок 73 ); ток проводимости от генератора проходит по одному из плеч излучателя, замыкается в виде токов смещения и через другое плечо возвращается в генератор.

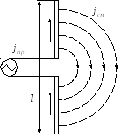
73. −Элементарный электрический излучатель

Малость длины излучателя по сравнению с длиной волны позволяет рассматривать его как точечный источник электромагнитных волн. Действительно, в произвольно расположенную точку наблюдения Р приходят сферические волны, возбуждаемые всеми элементарными участками излучающего проводника. Наибольшая геометрическая разность хода для крайних точек проводника составит , а разность фаз волн от этих точек, выраженная в радианах,. Согласно данной формуле, присистема излучает как бы единую сферическую волну и в этом смысле может считаться точечным источником.

10. Векторный электрический потенциал для элементарного электрического излучателя

Пользуясь результатами рассмотрения электродинамических потенциалов, вычислим поле векторного электрического потенциала, возбуждаемого элементарным электрическим излучателем в неограниченном свободном пространстве (,).

В соответствии с физической постановкой данной задачи воспользуемся сферической системой координат , в начальной точке которой расположим излучатель. Ввиду малости геометрических размеров излучателя радиус-вектор, входящий в формулу для электродинамического потенциала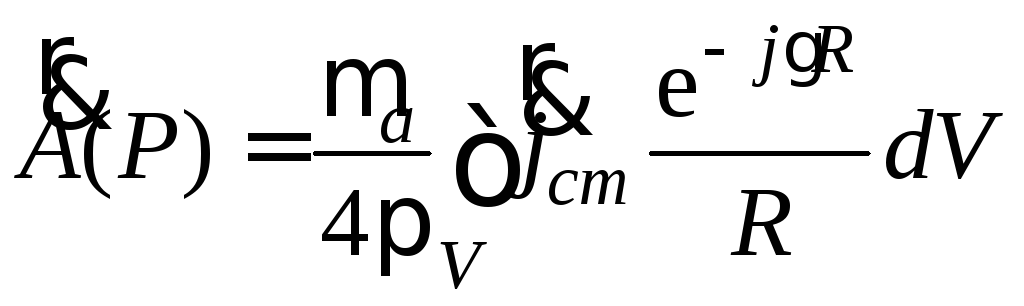, может считаться постоянным и равным сферической координате. Отсюда будем иметь

.

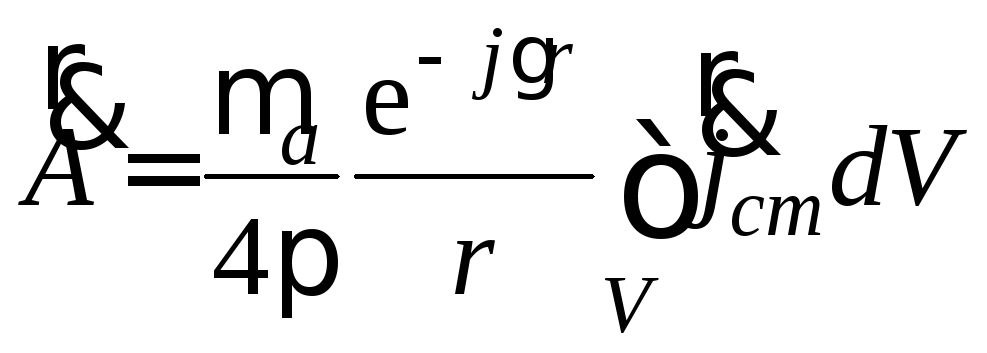Интегрирование вектора плотности стороннего тока по объему, занятому излучателем, представляет, на первый взгляд, логические трудности, поскольку, по определению, объем излучателя должен быть устремлен к нулю. Наиболее простой путь состоит в анализе физической размерности интеграла, входящего в последнюю формулу. Нетрудно проверить, что данный интеграл имеет размерность . Здесь известны амплитуда стороннего электрического тока в излучателеи его длина.

Требуемая размерность будет получена, если положить, откуда

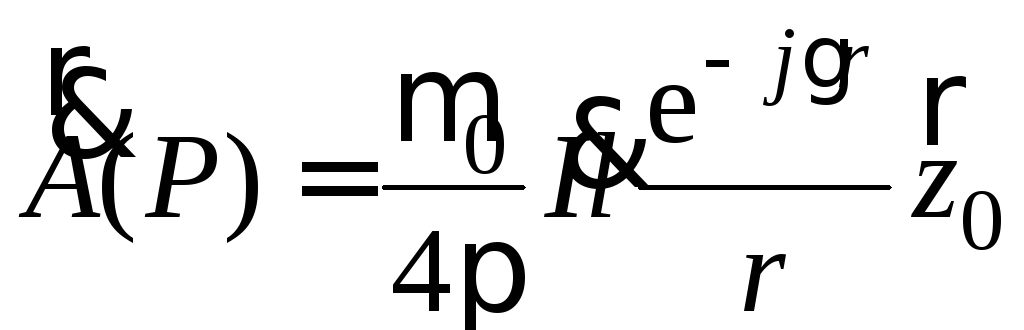
Единичный вектор i в двух последних формулах указывает на то, что ось элементарного излучателя направлена параллельно оси .

Для дальнейшего анализа необходимо знать разложение вектора в каждой точке пространства по ортам сферической системы координат. Способ подобного разложения показан на рисунке Рисунок 74 , из которого следует, что

,

.

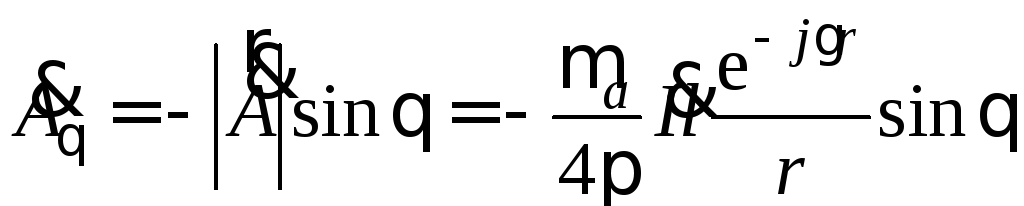Поскольку вектор электрического потенциала всюду направлен параллельно оси , его проекция на направление азимутального угла тождественно равна нулю, т.е..

74. −Определение сферических проекций векторного потенциала

1. Составляющие электромагнитного поля

Элементарный электрический излучатель представляет собой простейшую антенну, предназначенную для передачи электромагнитных колебаний в пространство. Поэтому большой интерес представляет нахождение структуры электромагнитного поля, возбуждаемого излучателем. Поскольку ранее был найден электрический векторный потенциал, то напряженности электрического и магнитного полей могут быть непосредственно выражены из потенциала через формулы перехода:

,.

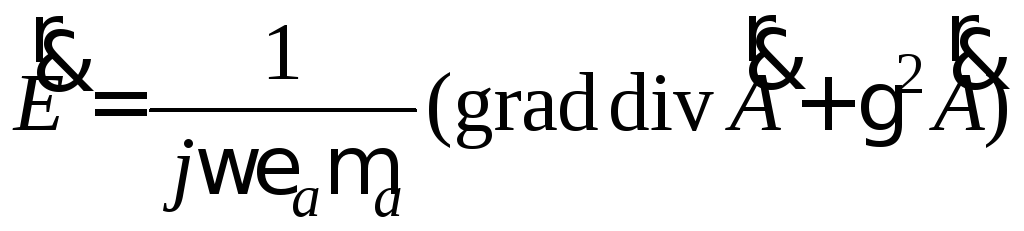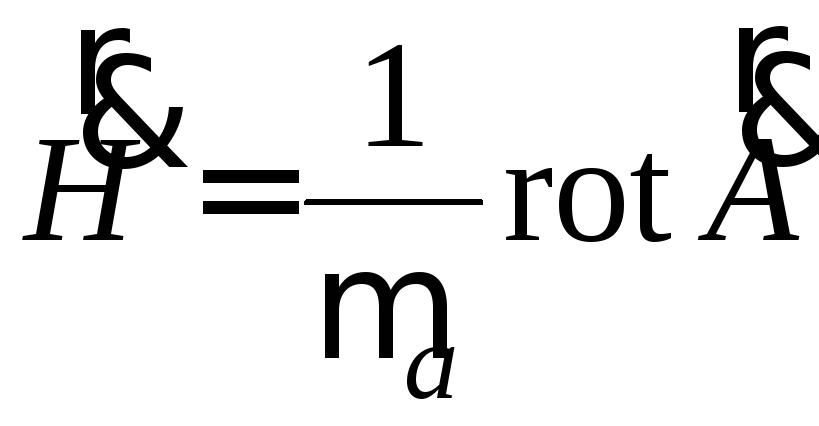Вычисление операции должно быть проведено в сферической системе координат. При этом вычисление значительно упрощается, поскольку, с одной стороны,, а с другой, отличные от нуля составляющиеине зависят от угла, так что. Проводя конкретные вычисления, получаем:

.

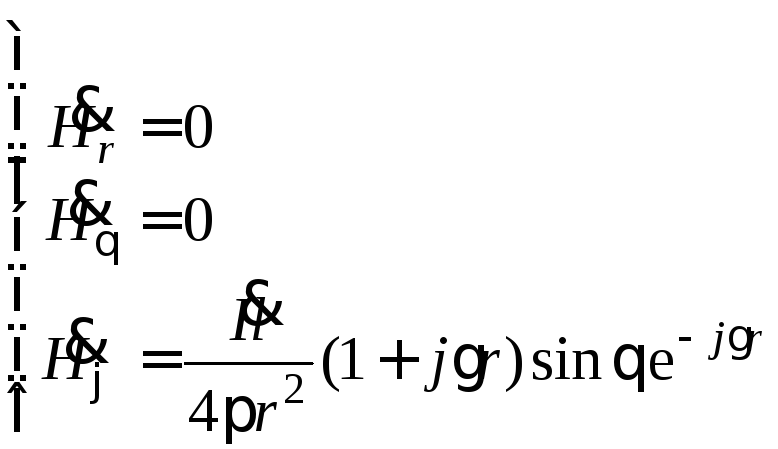Итак, в электромагнитном поле, возбуждаемом элементарным электрическим излучателем, присутствует вектор , обладающий единственной азимутальной составляющей. В этом смысле можно усмотреть некоторое сходство с магнитным полем постоянного электрического тока, протекающего по бесконечному линейному проводнику. Как известно, силовые линии магнитного поля при этом также имеют вид концентрических окружностей, охватывающих проводник.

Составляющие вектора могут быть определены из векторного потенциала по формулам перехода, или, что более просто, из первого уравнения Максвелла

.

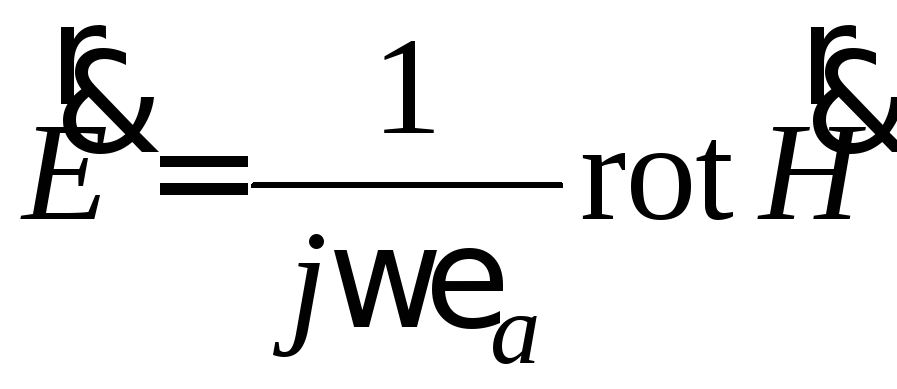Проведя соответствующие вычисления, будем иметь:

.
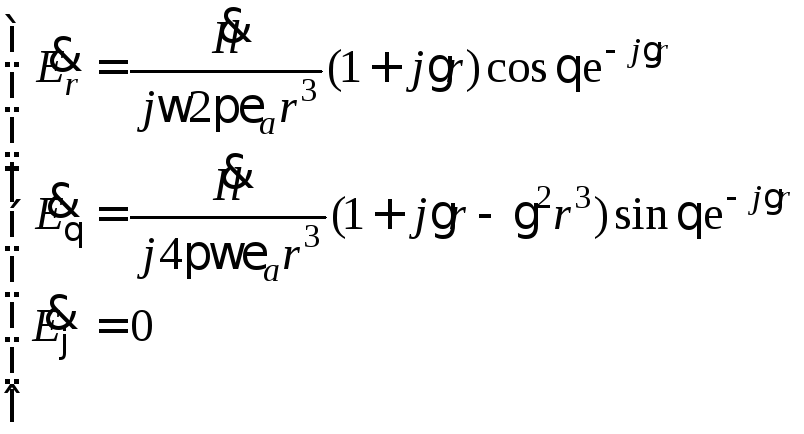