2. Калибровка потенциалов. Неоднородное уравнение Гельмгольца

Подставим соотношения найденные выражения векторов поля из потенциалов в первое уравнение Максвелла:

.

Раскрывая операцию , получаем

До сих по не накладывалось никаких ограничивающих условий на вид функций и. Потребуем теперь, чтобы оба потенциала удовлетворяли следующему соотношению:

Данная формула носит название соотношения калибровки потенциалов. Из-за произвольного выбора функций икалибровочное соотношение может быть удовлетворено в любом случае.

Заметим, что наложение условия калибровки значительно упрощает уравнение Максвелла с потенциалами, которое принимает вид

т. е. получается неоднородное уравнение Гсльмгольца относительно векторного электрического потенциала; в правой части его стоит известная функция распределения плотности стороннего электрического тока.

Отметим, что операция калибровки потенциалов позволяет выразить оба вектора электромагнитного поля через единственную функцию — электрический векторный потенциал. Действительно, воспользовавшись выражением калибровки, можно представить формулы перехода от потенциалов к векторам поля следующим образом:

,

.

3. Решение неоднородного уравнения Гельмгольца

В данном разделе на основе простых физических соображений будет показан способ нахождения решения неоднородного уравнения Гельмгольца.

Предположим, что сторонние электрические токи локализованы в некотором объеме (рисунок Рисунок 72 ); интенсивность возбуждаемого поля должна быть определена в точке, не принадлежащей.

72. −К решению неоднородного уравнения Гельмгольца

Рассмотрим элементарный объем , окружающий точку, лежащую внутри. Очевидно, что интенсивность поля в точке наблюдения, возникающего под действием токов, протекающих внутри, пропорциональна произведению. Здесь— некоторое среднее значение плотности стороннего тока, которое можно считать постоянным внутрииз-за малости последнего.

Дальнейший путь решения уравнения Гельмгольца заключается в следующем. Ввиду линейности уравнений Максвелла рассматриваемая система удовлетворяет принципу суперпозиции. В соответствии с этим принципом полное решение неоднородного уравнения Гельмгольца может быть получено как сумма всех воздействий, вызываемых в точке отдельными элементарными объемами. С физической точки зрения ясно, что по своей природе данные воздействия представляют собой сферические волны, распространяющиеся из отдельных точек объемаи уносящие электромагнитную энергию на бесконечность. Ранее было указано, что комплексная амплитуда сферической волны записывается в виде

.

Здесь, в соответствии с обозначениями, принятыми на рисунке Рисунок 72 , − текущее значение модуля радиус-вектора, соединяющего точкии.

Таким образом, с точностью до множителя пропорциональности величина элементарного воздействия

,

откуда полная величина электрического векторного потенциала в точке наблюдения может быть найдена при помощи суммирования:

.

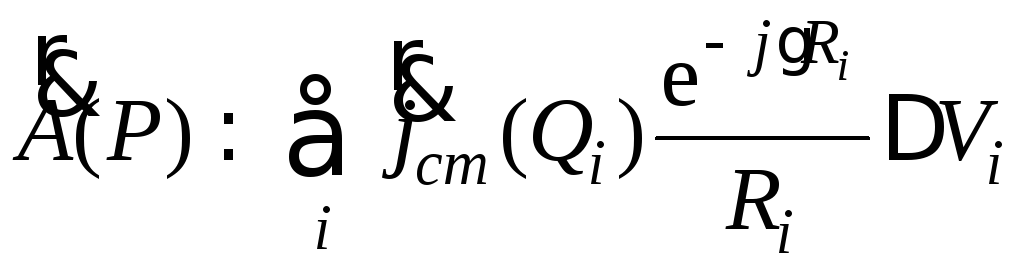Для того чтобы определить неизвестный коэффициент пропорциональности, необходимо совершить операцию предельного перехода, устремив к бесконечности число отдельных элементарных объемов. Как показано в курсе математической физики, строгий предельный переход

дает

Таким образом, получено интегральное представление общего решения неоднородного уравнения Гельмгольца.