8. Лекция 16

9. Решение неоднородных уравнений Максвелла

Во всех случаях, рассмотренных ранее, изучались так называемые однородные задачи электродинамики. При этом источники электромагнитного поля предполагались достаточно удаленными от области, в которой находилось электромагнитное поле. Во многих практических задачах часто требуется непосредственно связать величину сторонних электрических токов, являющихся источниками электромагнитного поля, с векторами ив любых точках пространства. Сюда относится, прежде всего, большинство задач из теории излучающих антенн. Другим примером может служить задача о возбуждении объемного резонатора с помощью штыря, щели, электронного пучка и т. д.

С математической точки зрения решение всех указанных задач сводится к решению неоднородной системы уравнений Максвелла, которая может быть записана следующим образом:

.

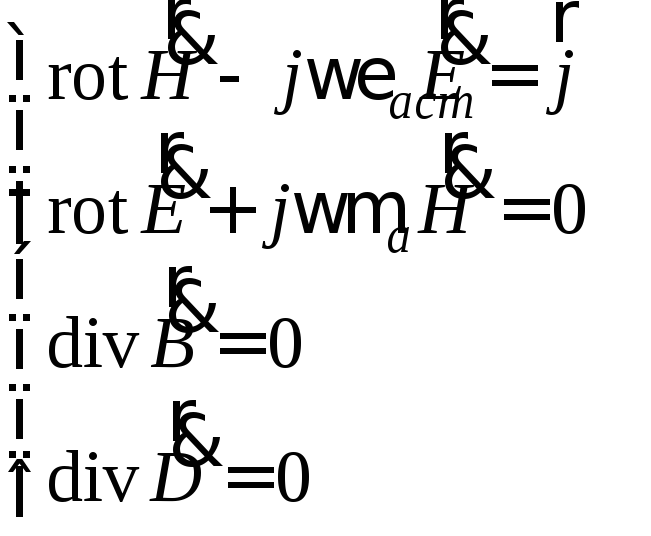Здесь для простоты предполагается, что плотность объемного заряда .

Подчеркнем, что в правой части этой системы записана плотность стороннего электрического тока, являющаяся известной векторной функцией пространственных координат. В этом смысле имеется прямая аналогия между неоднородной задачей электродинамики и задачей о нахождении токов в напряжений в электрической цепи, на которую воздействуют заданные сторонние ЭДС.

1. Векторный и скалярный потенциалы электромагнитного поля

Непосредственное решение системы уравнений Максвелла, как правило, весьма сложно, поскольку здесь определению подлежат шесть неизвестных составляющих векторов и. Поэтому бывает целесообразным найти некоторую вспомогательную функцию, знание которой позволило бы одновременно найти векторы напряженности электрического и магнитного полей. Подобные вспомогательные функции в электродинамике носят название потенциалов электромагнитного поля.

Отметим, прежде всего, что третьему уравнению Максвелла удовлетворяет векторное поле , определяемое по формуле

Здесь — некоторая векторная функция, носящая название электрического векторного потенциала. Подобное название обусловлено тем, что эта величина естественно используется в тех задачах, которые связаны с возбуждением электромагнитного поля электрическими сторонними токами. Аналогично

.

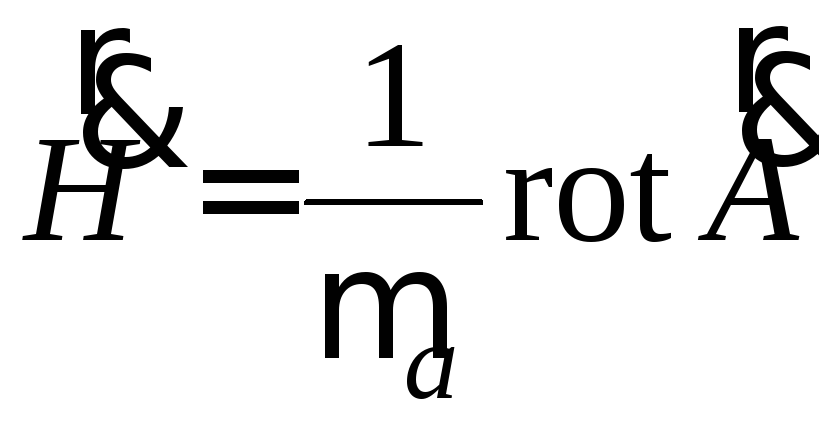Последние два соотношения весьма неопределенны, поскольку единственное условие, налагаемое на , — это дифференцируемость, обеспечивающая существование ротора данного векторного поля.

Попытаемся при помощи электрического векторного потенциала определить вектор напряженности электрического поля, для этого подставим выражение векторного потенциала во второе уравнение Максвелла:

,

т. е.

.

В силу известного тождества векторного анализа

вышеприведенное соотношение будет выполняться автоматически, если

Здесь — некоторая скалярная функция, называемая скалярным электрическим потенциалом.

Выбор знака в правой части последней формулы обусловлен тем, что в соответствии с известным соотношением электростатики для полей, не зависящих от времени, справедливо равенство

При этом сохраняется традиционное направление стрелок на силовых линиях электрического поля, при котором истоком поля считается положительный заряд.

Итак, в данном разделе найден способ выражения векторов электромагнитного поля через векторный и скалярный электрические потенциалы:

,