9. Общая задача о колебаниях в прямоугольном резонаторе. Классификация типов колебаний

Поставим задачу определить всю совокупность резонансных частот, которые соответствуют колебаниям различных типов в замкнутой металлической полости прямоугольной формы. Для этого обратимся вновь к изображению резонатора и положим, что ось является осью стоячей волны, а в поперечной плоскостиустанавливается распределение поля, отвечающее колебаниям типапрямоугольного волновода. Как уже было показано, условие резонанса приобретает вид.

Величина связана сдисперсионным соотношением

.

Поскольку

,

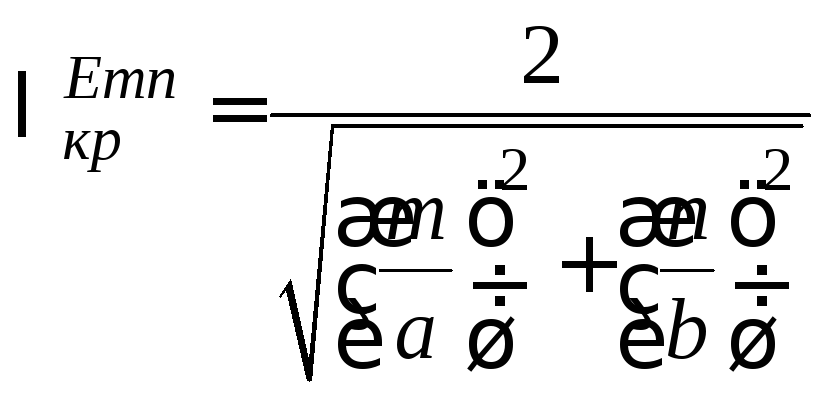то из дисперсионного соотношения получим

.

Если полагать, что по волноводу распространяется волна типа , то формула для резонансных длин волн будет полностью аналогична последнему уравнению.

Интересно отметить, что в формулу для резонансной длины волны размеры ,и, относящиеся к осям,исоответственно, входят совершенно равноправно. Поскольку известно, что некоторые из индексов типа колебаний могут равняться нулю, по крайней мере, для волн, естествен вопрос о том, возможны ли резонаторные типы колебаний с индексом. Согласно условию, поле не меняется на всем протяжении оси, вдоль которой расположены стенки длиной.

Если рассмотреть волноводную волну типа , то здесь силовые линии электрического вектора располагаются так, как это показано на рисунке Рисунок 60 (при,). Данный рисунок соответствует тому случаю, при котором тип колебаний является распространяющимся, т. е. при. Если же величинастремится к, то длина волны в волноводе устремляется к бесконечности и силовые линии электрического поля приобретают вид «нитей», параллельных оси. В пределе, при, электрическое поле обладает единственной-й составляющей, в силу чего граничные условия на двух идеально проводящих торцевых стенках будут выполняться автоматически независимо от расстояниямежду ними.

60. −К вопросу о существовании колебаний типов

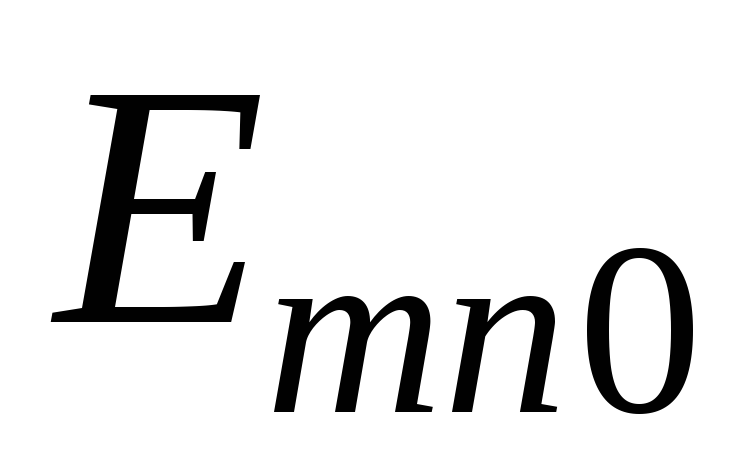
Таким образом, колебания типа в прямоугольном объемном резонаторе существуют. Если в уравнение для резонансных длин волн подставить значение, то будем иметь

.

Данная формула в точности совпадает с выражением для критической длины волны колебания типа в прямоугольном волноводе с размерами сечения. Это значит, что в объемном резонаторе с колебаниями типасуществует резонанс в поперечном сечении.

Рассмотрим теперь колебания типа в прямоугольном резонаторе. Здесь исходное волноводное колебание типа, по определению обладает только поперечным распределением электрического поля. Если составляющие поля не будут меняться вдоль оси, как это должно быть в случае колебания, то поле в любой точке резонатора должно быть тождественно равно нулю, поскольку граничные условия на торцевых стенках выполнены быть не могут. Таким образом, колебания типафизически не существуют.

Подытожим вопрос о классификации типов колебаний в прямоугольном объемном резонаторе. Уже известно, что данная классификация проводится следующим образом:

1) одна из осей резонатора принимается за ось стоячей волны;

2) определяется, какой волноводный тип колебаний, или, распространяется в регулярном волноводе, из которого образован объемный резонатор;

3) определяется величина — число стоячих полуволн, укладывающихся между торцевыми стенками.

В результате приходим к колебаниям типа или. Следует отметить, что данная классификация в значительной мере условна, поскольку она полностью определяется начальным выбором оси стоячей волны. Для иллюстрации этого положения на рисунке Рисунок 61 изображена уже знакомая картина поля для колебания типа.

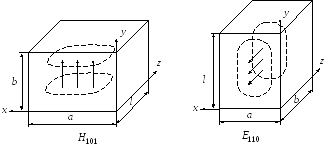
61. −К вопросу об условном характере классификации типов колебаний в объемном резонаторе

Если теперь осуществить поворот резонатора в пространстве таким образом, чтобы грань с размером была ориентирована вдоль оси, то этот же самый электромагнитный процесс должен быть обозначен как колебание типа. Легко проверить, что резонансные длины волн для названных типов колебаний тождественно равны.