2. Щелевая полосковая линия

Щелевая полосковая линия ЩПЛ − это двухпроводная полосковая линия (рисунок Рисунок 41 ), в которой электромагнитная волна распространяется вдоль щели между проводящими поверхностями, нанесенными на одну сторону подложки из диэлектрика. Анализ ЩПЛ показывает, что основной волной в линии является Н-волна, поскольку величина продольной составляющей напряженности электрического поля на порядок меньше величины поперечных составляющих, а все три составляющие магнитного поля сравнимы по величине. Как правило, основные характеристики ЩПЛ находят численно.

По сравнению с МПЛ в ЩПЛ:

1. более сильно проявляется дисперсия;

2. при одинаковых отношениях 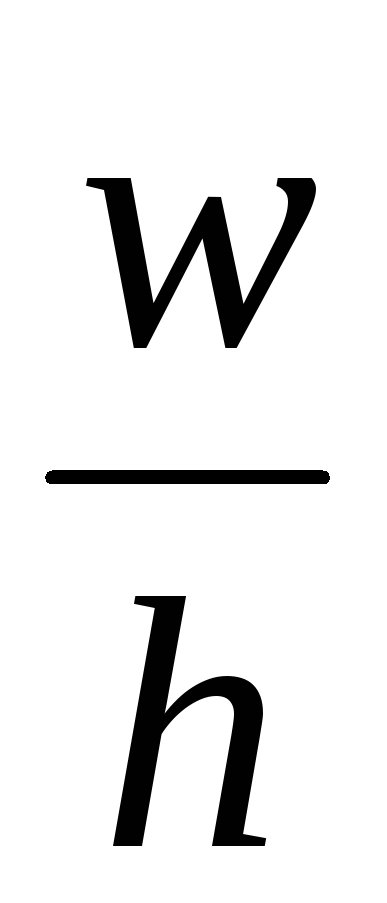иподложки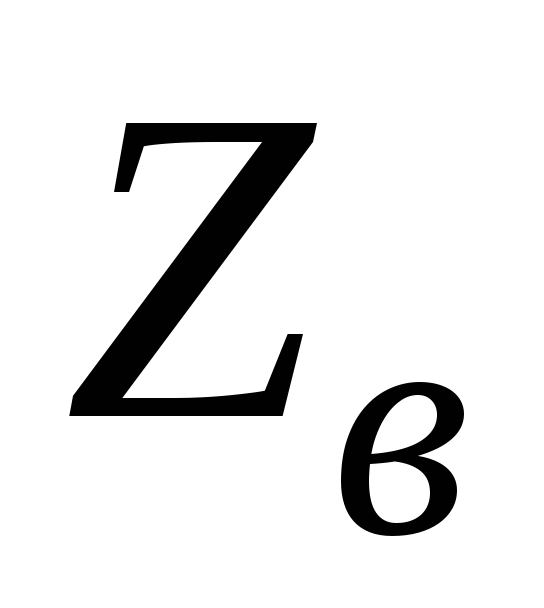в ЩПЛ больше, чем в МПЛ;

3. значительно ниже потери, поскольку ток проводимости рассредоточен по большей поверхности, чем в МПЛ.

При конструировании гибридных интегральных схем использование ЩПЛ позволяет более просто монтировать навесные элементы, в отличие от СПЛ и МПЛ.

41. −Щелевая полосковая линия

3. Линии поверхностной волны

Как было показано выше, при падении плоской электромагнитной волны на плоскую границу раздела двух диэлектриков, при определенных условиях происходит полное отражение волны. При этом как в первой, так и во второй средах возникает направляемая волна, распространяющаяся вдоль границы раздела. Во второй среде эта волна является поверхностной: ее поле экспоненциально убывает в направлении нормали к границе раздела. Поскольку фазовая скорость поверхностной волны меньше фазовой скорости ТЕМ-волны во второй среде, иногда эту волну называют медленной.

Рассмотрим некоторые линии передачи, в которых имеют место поверхностные волны.

Пусть на границу раздела двух диэлектриков, удовлетворяющих условию падает под угломплоская параллельно поляризованная волна (рисунок Рисунок 42 ).

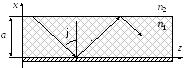
42. −Диэлектрическая пластина над идеально проводящей плоскостью

В результате полного внутреннего отражения падающая волна полностью отражается внутрь области 1, т.е. амплитуда поля в области 2 имеет экспоненциально затухающий характер. Если одну из плоскостей металлизировать (сделать идеально проводящей), то при должном выборе расстояния структура поля в областиможет быть сохранена. При этом прилегающий к плоскостислой диэлектрикабудет представлять собой направляющую систему открытого типа. В рассматриваемом случае в диэлектрическом слое распространяется Е-волна, структура поля (линии векторови) этой волны показана на рисунке Рисунок 43 ).

43. −Структура электромагнитного поля типа в диэлектрической пластине над идеально проводящей плоскостью

Отметим, что волну, распространяющуюся в диэлектрическом слое, ограниченном металлической плоскостью, можно рассматривать как суперпозицию парциальных волн, возникающих при полном отражении первичной ТЕМ-волны от поверхности идеального проводника () и от границы раздела двух диэлектриков (), как показано на рисунке Рисунок 42 . Полное отражение от границы разделавозможно при углах падения. Приусловия полного отражения не выполняются, и слой диэлектрика перестает играть роль волновода. Для слоя фиксированной толщиныусловиевыполняется при вполне определенном значении частоты, называемой критической частотой. Поэтому волна в рассматриваемой системе может распространяться только при.

При полном отражении нормально поляризованной плоской волны от плоской границы раздела двух диэлектриков образуется направляемая Н-волна. Рассуждая далее так же, как в случае параллельной поляризации, придем к аналогичной направляющей системе с волной типа Н.

Таким образом, в системе, состоящей из металлической пластины, покрытой слоем диэлектрика, при могут распространяться направляемые Е- и Н-волны. В общем случае (при конечной проводимости металлической пластины) будут распространяться и гибридные волны. Отметим некоторые особенности волн в такой направляющей системе: электромагнитная энергия переносится как в диэлектрике, так и прилегающей воздушной среде; амплитуды составляющих векторов поля в воздухе экспоненциально убывают по мере удаления от поверхности диэлектрика; средний за период поток энергии в направлении нормали к границе раздела «воздух-диэлектрик» равен нулю; фазовая скорость направляемых волн меньше фазовой скорости ТЕМ-волны в воздухе (поэтому, как уже отмечалось, такие волны называют медленными).

44. −Линия Губо и распределение поля в ней

Свойство границы раздела двух диэлектриков направлять поток электромагнитной энергии сохраняется и при ее цилиндрическом искривлении (рисунок Рисунок 44 ), т.е., одиночный провод, покрытый слоем диэлектрика, является волноводом, по которому можно передавать электромагнитную энергию. Такая линия известна в литературе как линия Губо. Основной волной в ней является волна типа Е, структура поля которой осесимметрична и аналогична такой же волне для плоской диэлектрической пластины с металлизацией. Затухание волны в линии определяется потерями энергии в металле и диэлектрическом слое. Чем толще слой диэлектрика и тоньше проводник, тем очевидно, выше затухание волны. Поэтому, например, в сантиметровом диапазоне волн толщину слоя выбирают достаточно малой − порядка 0,05...0,1 мм, а диаметр проводника берут не менее 1 мм. При этом коэффициент ослабления для основной волны в такой линии с диэлектрическим слоем из полистирола оказывается в 2-3 раза меньше, чем в прямоугольном волноводе на тех же частотах. Для метрового и дециметрового диапазонов волн (МГц) придиаметр волновода составляет 0,3...1 см.

В связи с тем, что часть электромагнитного поля распространяется в воздухе, окружающем волновод, то параметры волны, распространяющейся в линии Губо, существенно зависят от расположенных вблизи линии проводящих тел, а также от атмосферных условий, что приводит к ограниченному использованию ее на практике.

Можно выбрать толщину слоя диэлектрика таким образом, что он будет направлять волну и без ограничивающей его металлической пластины. Направляемую волну в этом случае можно представить в виде суперпозиции парциальных ТЕМ-волн, распространяющихся путем полного отражения от обеих границ раздела диэлектрика с менее плотной средой. В данном случае волноводом может служить плоская диэлектрическая пластина или круглый стержень.

Как показывает анализ, в круглом диэлектрическом волноводе могут существовать осесимметричные волны как типа Е, так и типа Н, а несимметричные волны могут быть только гибридными. Такие волны называются гибридными иволнами. Основной волной круглого диэлектрического волновода (для которой), является волна типа, структура ее показана на рисунке Рисунок 45 . Магнитные линии в горизонтальной плоскости имеют такую же структуру, как электрические в вертикальной. Внутри диэлектрического стержня структура поля напоминает волнув круглом волноводе, поэтому ее также называют волной типа.

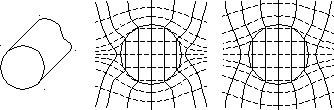
45. −Диэлектрический волновод и силовые линии поля для разной диэлектрической проницаемости

Диэлектрические волноводы различного сечения используются в технике миллиметровых и субмиллиметровых волн в качестве фидеров не очень большой протяженности, направляющих систем резонаторов и других элементов тракта. Вокруг волноводов необходимо обеспечивать свободную зону размеров в 2-3 радиуса волновода для беспрепятственного прохождения поверхностной волны. Это является недостатком диэлектрических волноводов и требует определенной конструкции их крепления.