
- •Лекции по курсу «Электродинамика и распространение радиоволн»
- •Лекция 9
- •Примеры линий передачи
- •Лекция 10
- •Распространение между двумя проводящими плоскостями
- •Падение плоской волны с параллельной поляризацией
- •Падение плоской волны с перпендикулярной поляризацией
- •Классификация направляемых волн
- •Фазовая скорость направляемых волн
- •Типы волн в волноводах
- •Критическая длина волны
- •Связь между продольными и поперечными составляющими поля
- •Лекция 11
- •Прямоугольный металлический волновод
- •Постановка задачи
- •Волны типа е в прямоугольном волноводе
- •Вычисление критической длины волны и длины волны в волноводе
- •Лекция 12
- •Волны типа н в прямоугольном волноводе
- •Волна типа
- •Лекция 13
- •Токи на стенках прямоугольного волновода
- •Излучающие и неизлучающие щели
- •Выбор размеров поперечного сечения прямоугольного волновода из условия одноволновой передачи
- •Волноводы п- и н-образной формы
- •Характеристические сопротивления волноводов
- •Круглый металлический волновод
- •Постановка задачи
- •Волны типа е в круглом волноводе
- •Волны типа н в круглом волноводе
- •Лекция 14
- •Линии передачи с волнами тем
- •Коаксиальная линия передачи
- •Волновое сопротивление
- •Полосковые линии передачи
- •Симметричная полосковая линия
- •Несимметричная полосковая линия
- •Лекция 15
- •Микрополосковая линия
- •Щелевая полосковая линия
- •Линии поверхностной волны
- •Световоды
- •Квазиоптические направляющие системы
- •Замедляющие системы
- •Объемные резонаторы
- •Объемный резонатор, образованный отрезком прямоугольного волновода
- •Общая задача о колебаниях в прямоугольном резонаторе. Классификация типов колебаний
- •Круглые объемные резонаторы
- •Некоторые способы возбуждения и включения объемных резонаторов
- •Добротность объемных резонаторов
- •Некоторые другие типы объемных резонаторов
- •Лекция 16
- •Решение неоднородных уравнений Максвелла
- •Векторный и скалярный потенциалы электромагнитного поля
- •Калибровка потенциалов. Неоднородное уравнение Гельмгольца
- •Решение неоднородного уравнения Гельмгольца
- •Элементарный электрический излучатель
- •Векторный электрический потенциал для элементарного электрического излучателя
- •Составляющие электромагнитного поля
- •Ближняя и дальняя зоны элементарного электрического излучателя
- •Диаграмма направленности элементарного электрического излучателя
- •Вычисление излученной мощности. Сопротивление излучения
- •Понятие о магнитном токе
- •Принцип перестановочной двойственности
- •Элементарный щелевой излучатель
Несимметричная полосковая линия
Несимметричная полосковая линия НПЛ
представляет собой двухпроводную
полосковую линию, состоящую из полоски
шириной
![]() и толщиной
и толщиной![]() ,
помещенной на расстоянии
,
помещенной на расстоянии![]() над экранирующей пластиной с шириной
над экранирующей пластиной с шириной![]() .
Пространство между проводниками и
экраном заполнено диэлектриком с
относительной диэлектрической
проницаемостью
.
Пространство между проводниками и
экраном заполнено диэлектриком с
относительной диэлектрической
проницаемостью![]() .
В случае, если в роли диэлектрика
выступает воздух, то такая линия обычно
называется НПЛ.
.
В случае, если в роли диэлектрика
выступает воздух, то такая линия обычно
называется НПЛ.
Как и в случае с СПЛ, волновое сопротивление
НПЛ обычно рассчитывают из погонной
емкости линии. Приведем окончательные
приближенные формулы для
![]() ,
позволяющие проводить расчеты с
относительной погрешностью не более
0,6% при нулевой толщине полоски
,
позволяющие проводить расчеты с
относительной погрешностью не более
0,6% при нулевой толщине полоски![]() :
:
при
![]()
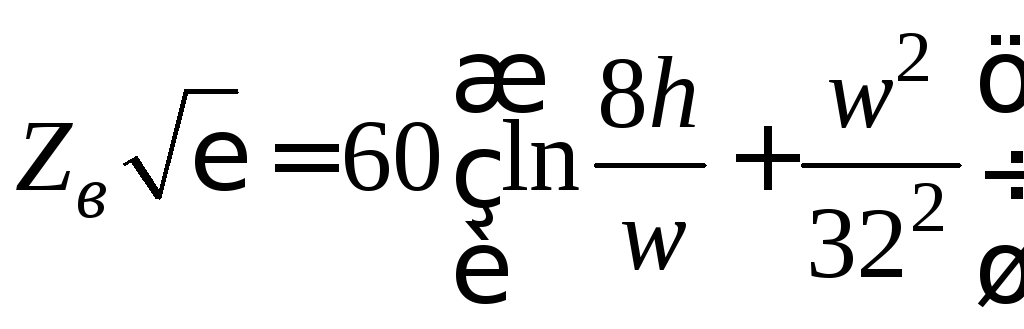
при
![]()
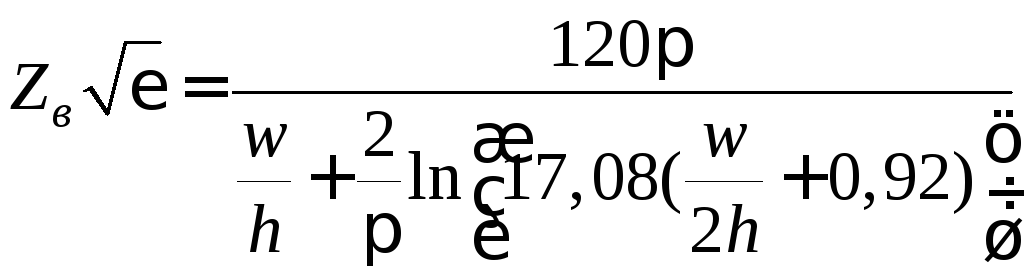 .
.
Лекция 15
Микрополосковая линия
На практике наиболее широкое применение
находит несколько измененная конструкция
НПЛ, называемая микрополосковой линией
(рисунок Рисунок 40 ). Она отличается от
НПЛ тем, что между полоской и экранирующей
пластиной помещается подложка из
диэлектрика с параметрами
![]() ,
,![]() ,
,![]() ,
а над полоской находится диэлектрик с
параметрами
,
а над полоской находится диэлектрик с
параметрами![]() ,
,![]() ,
,![]() .
Как правило, над полоской используется
воздушное заполнение (
.
Как правило, над полоской используется
воздушное заполнение (![]() ,
,![]() ).
Если сравнить передачу энергии по НПЛ
и МПЛ, то окажется, что для МПЛ уровень
излучения энергии в окружающее
пространство гораздо ниже, чем для НПЛ,
что связано с концентрацией
электромагнитного поля в диэлектрике
подложки, особенно при больших значениях
).
Если сравнить передачу энергии по НПЛ
и МПЛ, то окажется, что для МПЛ уровень
излучения энергии в окружающее
пространство гораздо ниже, чем для НПЛ,
что связано с концентрацией
электромагнитного поля в диэлектрике
подложки, особенно при больших значениях![]() .
.
При передаче энергии по МПЛ электромагнитное
поле существует не только в подложке,
но и в воздухе. При этом появляются
продольные составляющие векторов поля,
т.е. по МПЛ в общем случае энергия
переносится гибридными волнами (![]() и
и![]() ).
Однако, как показывает анализ, при
достаточно малых по сравнению с длиной
волны размерах поперечного сечения МПЛ
для основной волны величина продольных
составляющих векторов поля оказывается
на порядок меньше величины поперечных
составляющих, и ими можно пренебречь.
Поэтому приближенно можно считать, что
структура основной волны в МПЛ (рисунок
Рисунок 40 ), получившей название квази-ТЕМ,
совпадает по структуре с ТЕМ-волной.
).
Однако, как показывает анализ, при
достаточно малых по сравнению с длиной
волны размерах поперечного сечения МПЛ
для основной волны величина продольных
составляющих векторов поля оказывается
на порядок меньше величины поперечных
составляющих, и ими можно пренебречь.
Поэтому приближенно можно считать, что
структура основной волны в МПЛ (рисунок
Рисунок 40 ), получившей название квази-ТЕМ,
совпадает по структуре с ТЕМ-волной.
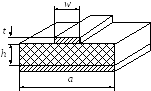

−Микрополосковая линия и распределение поля в ней
Волна квази-ТЕМ, как и ТЕМ-волна, может
распространяться на любых частотах,
для нее
![]() .
Причем, поскольку квази-ТЕМ волна
переносит часть энергии в подложке, а
часть в воздухе, ее фазовая скорость
удовлетворяет неравенству
.
Причем, поскольку квази-ТЕМ волна
переносит часть энергии в подложке, а
часть в воздухе, ее фазовая скорость
удовлетворяет неравенству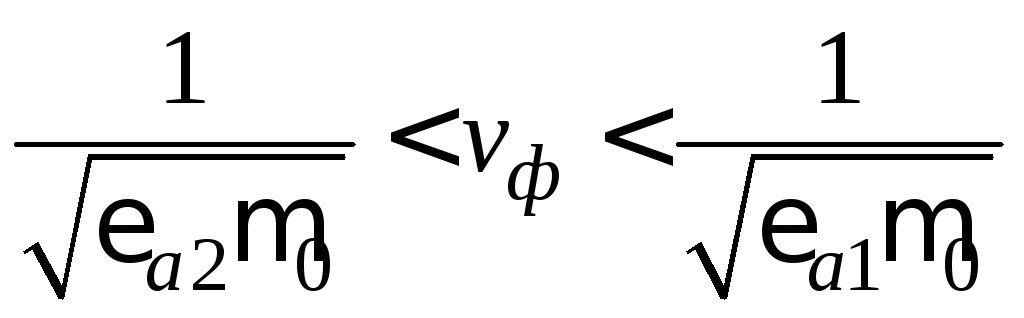 (напомним, что скорость света в идеальном
диэлектрике с
(напомним, что скорость света в идеальном
диэлектрике с![]() определяется как
определяется как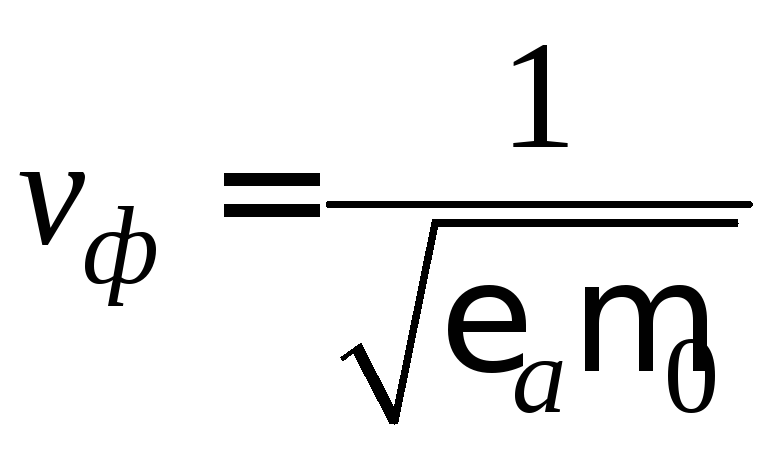 ).
Чем больше энергии переносится в
подложке, тем больше фазовая скорость
).
Чем больше энергии переносится в
подложке, тем больше фазовая скорость![]() к скорости света в подложке, и наоборот.
Обычно при определении основных
характеристик волн в линиях с поперечно
неоднородным диэлектрическим заполнением
вводят эффективную относительную и
эффективную абсолютную диэлектрические
проницаемости линии
к скорости света в подложке, и наоборот.
Обычно при определении основных
характеристик волн в линиях с поперечно
неоднородным диэлектрическим заполнением
вводят эффективную относительную и
эффективную абсолютную диэлектрические
проницаемости линии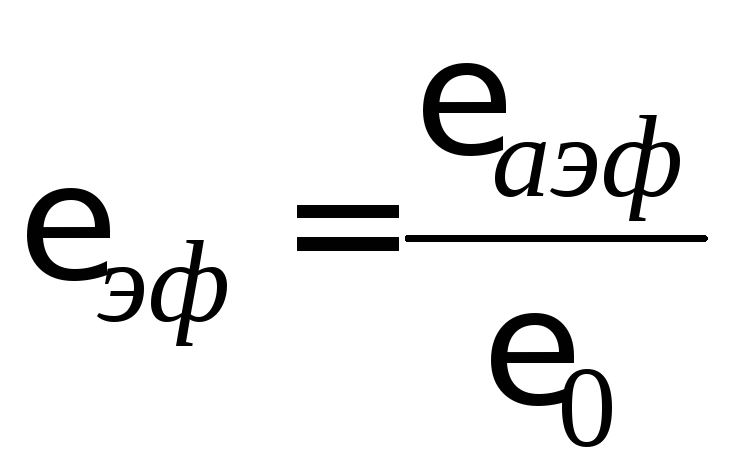 ,
связанные с фазовой скоростью волны
,
связанные с фазовой скоростью волны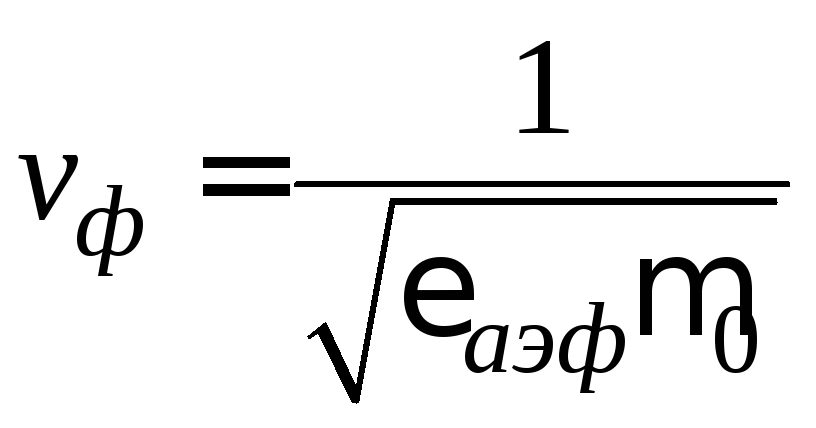 ,
причем
,
причем![]() .
При
.
При![]() и
и![]() эффективную проницаемость для волны
квази-ТЕМ в МПЛ можно определить по
формуле, справедливой для
эффективную проницаемость для волны
квази-ТЕМ в МПЛ можно определить по
формуле, справедливой для![]() :
:
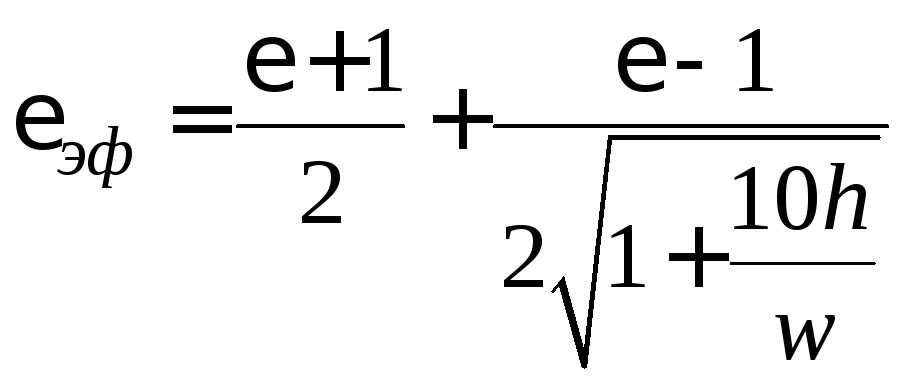 .
.
Отсюда следует, что фазовая скорость
квази-ТЕМ волны зависит не только от
параметров заполняющего диэлектрика,
но и от геометрических размеров линии
(последнее свойство характерно для Н-
и Е-волн в волноводах): при увеличении
![]() и
и![]() или уменьшении
или уменьшении![]() фазовая скорость квази-ТЕМ волны в МПЛ
уменьшается, поскольку при подобном
изменении увеличивается количество
энергии, переносимой волной в подложке,
и наоборот. Все основные характеристики
квази-ТЕМ волны рассчитываются по
формулам для ТЕМ-волн путем замены
фазовая скорость квази-ТЕМ волны в МПЛ
уменьшается, поскольку при подобном
изменении увеличивается количество
энергии, переносимой волной в подложке,
и наоборот. Все основные характеристики
квази-ТЕМ волны рассчитываются по
формулам для ТЕМ-волн путем замены![]() на
на![]() .
Длина волны квази-ТЕМ в МПЛ на частоте
.
Длина волны квази-ТЕМ в МПЛ на частоте![]() рассчитывается по формуле
рассчитывается по формуле
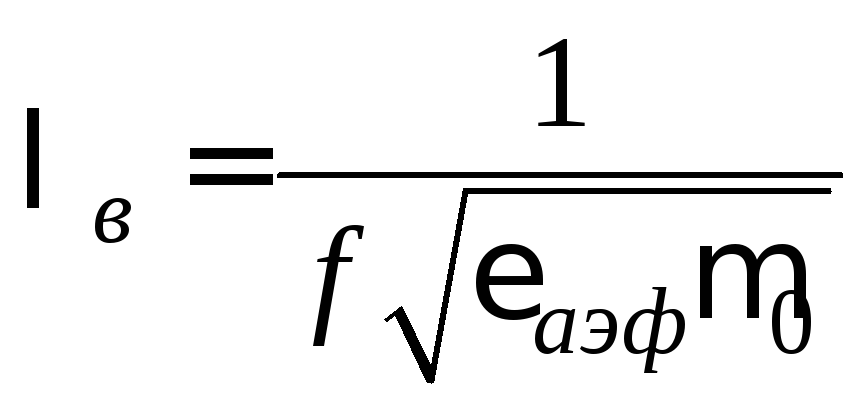 ,
,
Волновое сопротивление МПЛ рассчитывается
по формулам для
![]() НПЛ, где
НПЛ, где![]() заменяется на
заменяется на![]() .
Как и в случае с СПЛ, волновое сопротивление
МПЛ уменьшается при увеличении
.
Как и в случае с СПЛ, волновое сопротивление
МПЛ уменьшается при увеличении![]() ,
увеличении
,
увеличении![]() и
и![]() ,
и уменьшении
,
и уменьшении![]() .
.
