
- •Лекции по курсу «Электродинамика и распространение радиоволн»
- •Лекция 9
- •Примеры линий передачи
- •Лекция 10
- •Распространение между двумя проводящими плоскостями
- •Падение плоской волны с параллельной поляризацией
- •Падение плоской волны с перпендикулярной поляризацией
- •Классификация направляемых волн
- •Фазовая скорость направляемых волн
- •Типы волн в волноводах
- •Критическая длина волны
- •Связь между продольными и поперечными составляющими поля
- •Лекция 11
- •Прямоугольный металлический волновод
- •Постановка задачи
- •Волны типа е в прямоугольном волноводе
- •Вычисление критической длины волны и длины волны в волноводе
- •Лекция 12
- •Волны типа н в прямоугольном волноводе
- •Волна типа
- •Лекция 13
- •Токи на стенках прямоугольного волновода
- •Излучающие и неизлучающие щели
- •Выбор размеров поперечного сечения прямоугольного волновода из условия одноволновой передачи
- •Волноводы п- и н-образной формы
- •Характеристические сопротивления волноводов
- •Круглый металлический волновод
- •Постановка задачи
- •Волны типа е в круглом волноводе
- •Волны типа н в круглом волноводе
- •Лекция 14
- •Линии передачи с волнами тем
- •Коаксиальная линия передачи
- •Волновое сопротивление
- •Полосковые линии передачи
- •Симметричная полосковая линия
- •Несимметричная полосковая линия
- •Лекция 15
- •Микрополосковая линия
- •Щелевая полосковая линия
- •Линии поверхностной волны
- •Световоды
- •Квазиоптические направляющие системы
- •Замедляющие системы
- •Объемные резонаторы
- •Объемный резонатор, образованный отрезком прямоугольного волновода
- •Общая задача о колебаниях в прямоугольном резонаторе. Классификация типов колебаний
- •Круглые объемные резонаторы
- •Некоторые способы возбуждения и включения объемных резонаторов
- •Добротность объемных резонаторов
- •Некоторые другие типы объемных резонаторов
- •Лекция 16
- •Решение неоднородных уравнений Максвелла
- •Векторный и скалярный потенциалы электромагнитного поля
- •Калибровка потенциалов. Неоднородное уравнение Гельмгольца
- •Решение неоднородного уравнения Гельмгольца
- •Элементарный электрический излучатель
- •Векторный электрический потенциал для элементарного электрического излучателя
- •Составляющие электромагнитного поля
- •Ближняя и дальняя зоны элементарного электрического излучателя
- •Диаграмма направленности элементарного электрического излучателя
- •Вычисление излученной мощности. Сопротивление излучения
- •Понятие о магнитном токе
- •Принцип перестановочной двойственности
- •Элементарный щелевой излучатель
Волны типа е в круглом волноводе
Задача о распространении по круглому
металлическому волноводу колебаний
электрического типа, характеризующихся
условиями
![]() ,
,![]() ,
сводится к решению уравнения Гельмгольца
,
сводится к решению уравнения Гельмгольца
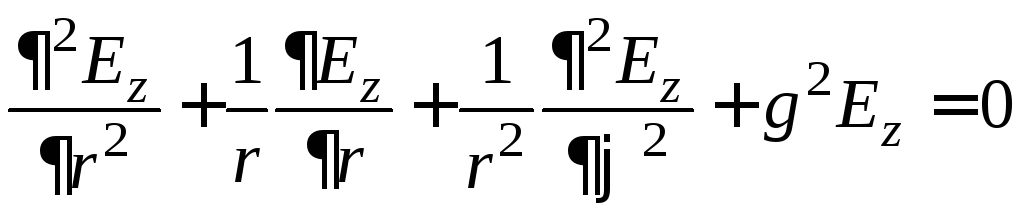
при граничных условиях, обеспечивающих
обращение в нуль тангенциальных
составляющих электрического вектора
на стенках волновода. Очевидно, что из
трех возможных составляющих поля
![]() ,
а именно:
,
а именно:![]() ,
,![]() ,
,![]() касательными к стенкам волновода могут
быть только составляющие
касательными к стенкам волновода могут
быть только составляющие![]() и
и![]() .
Поэтому необходимо потребовать
.
Поэтому необходимо потребовать
![]() ,
,
![]()
Из формул перехода от продольных
составляющих к поперечным непосредственно
следует, что два последних условия не
являются независимыми. Так, составляющая
![]() .
пропорциональная частной производной
.
пропорциональная частной производной![]() ,
обратится в нуль при постоянстве
,
обратится в нуль при постоянстве![]() на контуре волновода. Поэтому физичски
достаточно, чтобы на металлических
стенках волновода выполнялось граничное
условие
на контуре волновода. Поэтому физичски
достаточно, чтобы на металлических
стенках волновода выполнялось граничное
условие![]() .
Вместе с уравнением Гельмгольца оно
образует однородную краевую задау
Дирихле.
.
Вместе с уравнением Гельмгольца оно
образует однородную краевую задау
Дирихле.
Будем решать эту задачу методом разделения переменных. Положим, что
![]()
где
![]() ,
,![]() − неизвестные функции только от
− неизвестные функции только от![]() и
и![]() соответственно, подлежащие определению.
соответственно, подлежащие определению.
Подставляя последнее выражение в уравнение Гельмгольца, будем иметь
![]()
Преобразуем это уравнение таким образом,
чтобы в левой части располагались
функции только от
![]() ,
а в правой—только от
,
а в правой—только от![]() .
Для этого левую и правую части следует
разделить на произведение
.
Для этого левую и правую части следует
разделить на произведение![]() :
:
![]()
Для того чтобы это уравнение выполнялось
тождественно при любых
![]() и
и![]() ,
необходимо выполнение равенства
,
необходимо выполнение равенства
![]()
Решением этого уравнения служат равенства
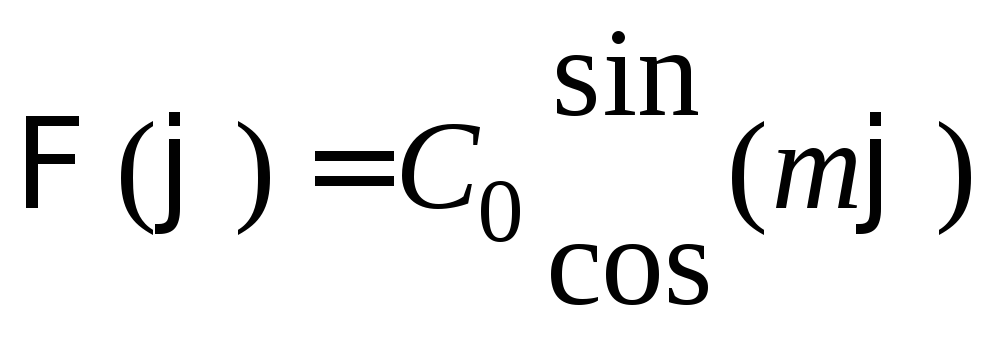
а также их любая линейная комбинация
при произвольном коэффициенте
![]() .
Выбор той или иной из этих функций
безразличен в силу симметрии волновода
по угловой координате
.
Выбор той или иной из этих функций
безразличен в силу симметрии волновода
по угловой координате![]() .
Однако для того чтобы выполнялось
физически очевидное требование
периодичности решения по углу
.
Однако для того чтобы выполнялось
физически очевидное требование
периодичности решения по углу![]() с периодом не более
с периодом не более![]() ,
,![]() должно быть целым числом или нулем (в
последнем случае приемлемо только
косинусоидальное решение).
должно быть целым числом или нулем (в
последнем случае приемлемо только
косинусоидальное решение).
Число
![]() служит одним из индексов типа волны
служит одним из индексов типа волны
Рассмотрим теперь левую часть волнового уравнения с целью получить новое уравнение, описывающее радиальное распределение поля. Из последних выкладок имеем
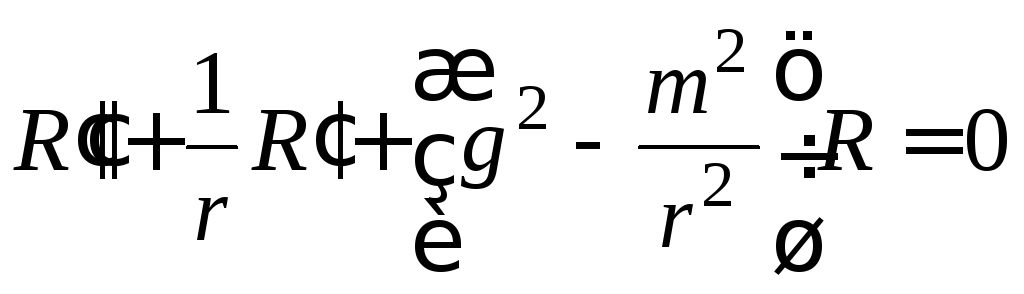
Целесообразно преобразовать это уравнение к несколько другому виду, введя безразмерную независимую переменную
![]() ,
,
откуда получим
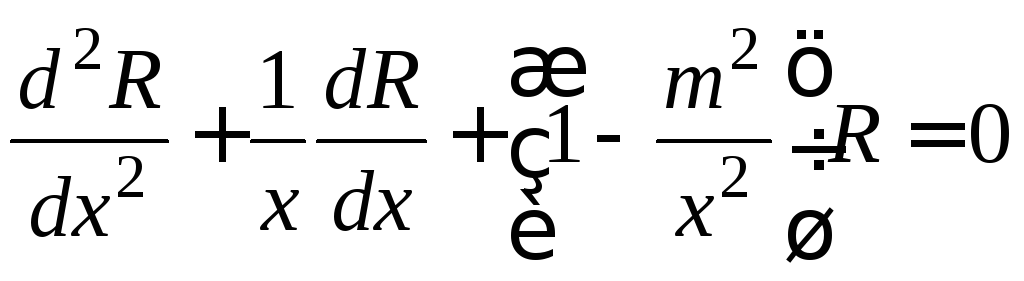 .
.
Данное уравнение хорошо изучено в математической физике и носит название уравнения Бесселя. С математической точки зрения уравнение Бесселя является линейным дифференциальным уравнением второго порядка с переменными коэффициентами.
Цилиндрические функции. Так называют частные решения уравнения Бесселя. К ним относятся:
![]() — функция Бесселя или цилиндрическая
функция первого рода индекса
— функция Бесселя или цилиндрическая
функция первого рода индекса![]() ;
;
![]() — функция Неймана или цилиндрическая
функция второго рода индекса
— функция Неймана или цилиндрическая
функция второго рода индекса![]() .
.
Обе цилиидрические функции являются линейно независимыми, поэтому общее решение уравнения Бесселя записывается в виде
![]() ,
,
где
![]() и
и![]() — некоторые произвольные постоянные.
— некоторые произвольные постоянные.
Цилиндрические функции первого и второго рода в цилиндрической системе координат играют ту же роль, что синусоидальная и косинусоидальная функции в декартовой прямоугольной системе. Из примерного вида графиков этих функций, представленного на рисунке Рисунок 30 , видно, что они имеют много общего с гармоническими функциями. Однако имеются и существенные различия:
1) цилиндрические функции в отличие от синусоидальной и косинусоидальной не являются периодическими;
2) амплитуда этих функций также не
постоянна, а уменьшается с ростом
независимой переменной
![]() ;
;
3) чем больше индекс
![]() ,
тем сильнее смещены цилиндрические
функции по оси
,
тем сильнее смещены цилиндрические
функции по оси![]() ;
на рисунке это показано применительно
к функциям
;
на рисунке это показано применительно
к функциям![]() и
и![]() ;
;
4) вблизи начала координат функция
![]() неограниченно велика:
неограниченно велика:
![]()
Поэтому при решений задач в круглых
волноводах необходимо полагать
![]() ,
ибо присутствие на оси волновода при
,
ибо присутствие на оси волновода при
![]() бесконечно высоких напряженностей
полей физически нереально.
бесконечно высоких напряженностей
полей физически нереально.
Для решения большинства практических
задач наибольший интерес представляют
простейшие цилиндрические функции
![]() и
и![]() .
В теории цилиндрических функций показано,
что между ними существует следующее
соотношение:
.
В теории цилиндрических функций показано,
что между ними существует следующее
соотношение:
![]()
На рисунке Рисунок 30 представлены графики этих функций. Для дальнейшего наибольший интерес представляют те значения аргумента, при которых обращаются в нуль сами функции Бесселя, либо первые производные. Введем следующие обозначения:
![]() —
—![]() -й
корень уравнения
-й
корень уравнения![]() ,
,
![]() —
—![]() -й
корень уравнения
-й
корень уравнения![]() .
.
Анализируя представленные графики,
легко видеть, что функция
![]() первый раз пересекает ось абсцисс в
точке, приблизительно равной 2,405. В
соответствии с принятой договоренностью
данная точка обозначается как
первый раз пересекает ось абсцисс в
точке, приблизительно равной 2,405. В
соответствии с принятой договоренностью
данная точка обозначается как![]() .
Аналогично, первый положительный
максимум функции
.
Аналогично, первый положительный
максимум функции![]() приходится на значение аргумента 1,841,
которое должно быть обозначено как
приходится на значение аргумента 1,841,
которое должно быть обозначено как![]() .
.
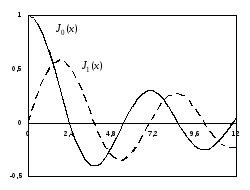
−Функции Бесселя
Теперь можно вновь вернуться к исследованию воли электрического типа. В соответствии с методом разделения переменных амплитуда продольной составляющей напряженности электрического поля запишется в виде
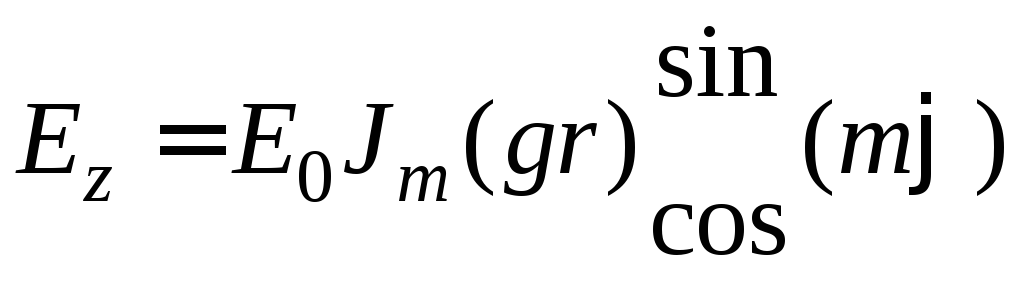
Здесь поперечное волновое число
![]() пока еще не определено. Чтобы найти его,
заметим, что граничное условие
пока еще не определено. Чтобы найти его,
заметим, что граничное условие
![]()
будет выполнено в том случае, если числа принадлежат бесконечной дискретной последовательности, удовлетворяющей соотношению
![]() ,
,
откуда
![]() .
.
Номер корня
![]() является вторым индексом волны
является вторым индексом волны![]() .
Итак, окончательно комплексная амплитуда
составляющей
.
Итак, окончательно комплексная амплитуда
составляющей![]() для колебания типа
для колебания типа![]() принимает вид:
принимает вид:
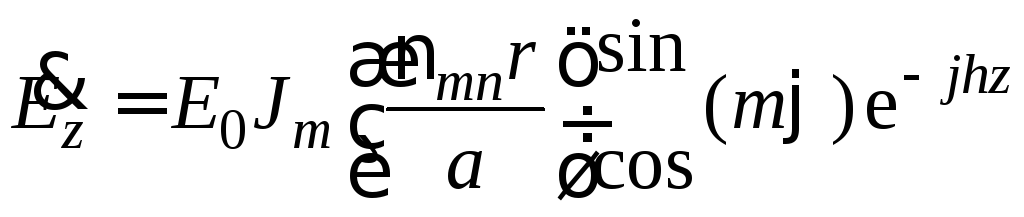
Физический смысл индексов
![]() и
и![]() очень прост:
очень прост:![]() означает число вариаций поля по угловой
координате
означает число вариаций поля по угловой
координате![]() ,
а
,
а![]() — число вариаций по радиальной координате
— число вариаций по радиальной координате![]() .
В частном случае
.
В частном случае![]() поля по углу
поля по углу![]() не изменяются, и такие типы волн называют
симметричными.
не изменяются, и такие типы волн называют
симметричными.
Критические длины волн находятся на основании того же самого принципа, что и в случае прямоугольного волновода:
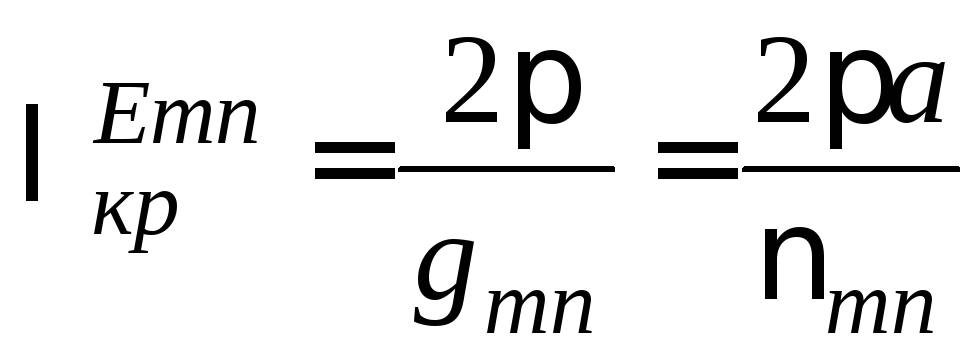 .
.
Формулы для вычисления длины волны в волноводе и фазовой скорости имеют ту же структуру, что и в теории прямоугольного волновода:
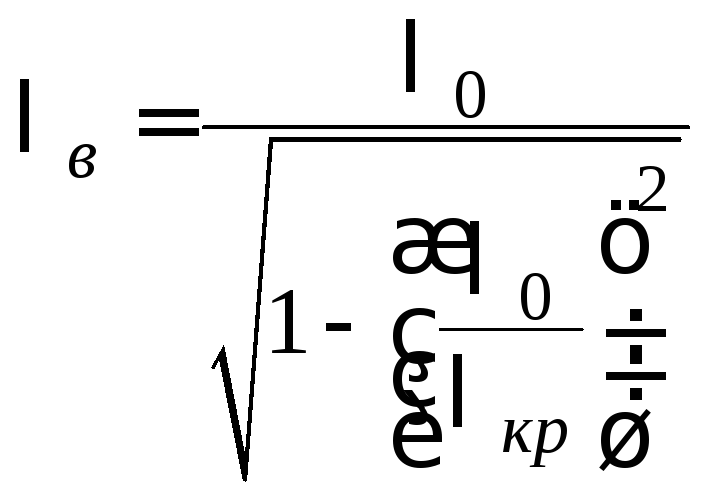 ,
,
Поперечные составляющие полей для любой
волны типа
![]() легко находятся из выражения для
продольной составляющей
легко находятся из выражения для
продольной составляющей![]() и формул перехода. Покажем это на примере
часто употребляемой простейшей
симметричной волны типа
и формул перехода. Покажем это на примере
часто употребляемой простейшей
симметричной волны типа![]() .
Здесь
.
Здесь
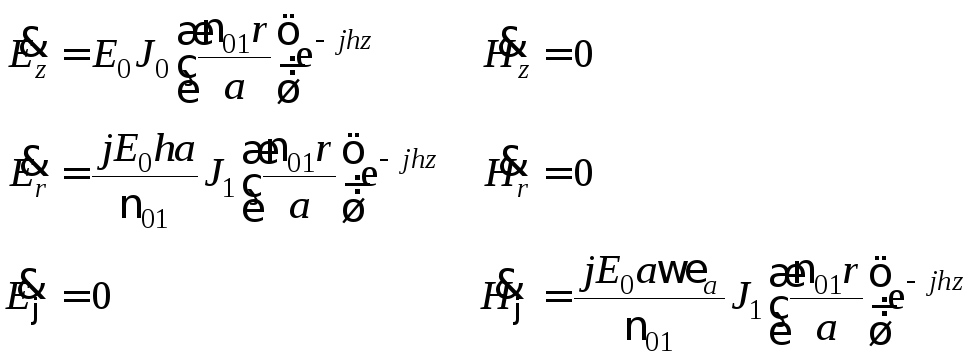
Картина распределения полей в волноводе,
построенная по этим формулам, показана
на рисунке. Интересно отметить, что
данная структура поля может быть получена
непрерывной деформацией структуры типа
![]() в прямоугольном волноводе.
в прямоугольном волноводе.
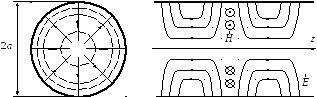
− Картина силовых линий волны типа
 в круглом волноводе
в круглом волноводе
