
- •Лекции по курсу «Электродинамика и распространение радиоволн»
- •Лекция 9
- •Примеры линий передачи
- •Лекция 10
- •Распространение между двумя проводящими плоскостями
- •Падение плоской волны с параллельной поляризацией
- •Падение плоской волны с перпендикулярной поляризацией
- •Классификация направляемых волн
- •Фазовая скорость направляемых волн
- •Типы волн в волноводах
- •Критическая длина волны
- •Связь между продольными и поперечными составляющими поля
- •Лекция 11
- •Прямоугольный металлический волновод
- •Постановка задачи
- •Волны типа е в прямоугольном волноводе
- •Вычисление критической длины волны и длины волны в волноводе
- •Лекция 12
- •Волны типа н в прямоугольном волноводе
- •Волна типа
- •Лекция 13
- •Токи на стенках прямоугольного волновода
- •Излучающие и неизлучающие щели
- •Выбор размеров поперечного сечения прямоугольного волновода из условия одноволновой передачи
- •Волноводы п- и н-образной формы
- •Характеристические сопротивления волноводов
- •Круглый металлический волновод
- •Постановка задачи
- •Волны типа е в круглом волноводе
- •Волны типа н в круглом волноводе
- •Лекция 14
- •Линии передачи с волнами тем
- •Коаксиальная линия передачи
- •Волновое сопротивление
- •Полосковые линии передачи
- •Симметричная полосковая линия
- •Несимметричная полосковая линия
- •Лекция 15
- •Микрополосковая линия
- •Щелевая полосковая линия
- •Линии поверхностной волны
- •Световоды
- •Квазиоптические направляющие системы
- •Замедляющие системы
- •Объемные резонаторы
- •Объемный резонатор, образованный отрезком прямоугольного волновода
- •Общая задача о колебаниях в прямоугольном резонаторе. Классификация типов колебаний
- •Круглые объемные резонаторы
- •Некоторые способы возбуждения и включения объемных резонаторов
- •Добротность объемных резонаторов
- •Некоторые другие типы объемных резонаторов
- •Лекция 16
- •Решение неоднородных уравнений Максвелла
- •Векторный и скалярный потенциалы электромагнитного поля
- •Калибровка потенциалов. Неоднородное уравнение Гельмгольца
- •Решение неоднородного уравнения Гельмгольца
- •Элементарный электрический излучатель
- •Векторный электрический потенциал для элементарного электрического излучателя
- •Составляющие электромагнитного поля
- •Ближняя и дальняя зоны элементарного электрического излучателя
- •Диаграмма направленности элементарного электрического излучателя
- •Вычисление излученной мощности. Сопротивление излучения
- •Понятие о магнитном токе
- •Принцип перестановочной двойственности
- •Элементарный щелевой излучатель
Выбор размеров поперечного сечения прямоугольного волновода из условия одноволновой передачи
Как было показано, в прямоугольном волноводе возможно существование бесконечного числа типов волн, отличающихся друг от друга структурой электрического и магнитного полей, критическими частотами, фазовой скоростью и другими параметрами. Однако при конструировании линий передачи обычно принимают все меры к тому, чтобы энергия переносилась каким-либо одним типом волны. Объясняется это тем, что различным типам волн соответствуют различные групповые скорости. Поэтому при передаче сигнала несколькими типами волн один и тот же сигнал приходит в точку приема в вине нескольких смещенных по времени сигналов, что приводит к его искажению и увеличению уровня шумов. Характер искажений зависит от способа модуляции, вида и скорости передаваемой информации и других факторов.
Передачу энергии одним типом волны
можно обеспечить, если в качестве этого
типа использовать основную волну,
имеющую наибольшую
![]() .
Для этого достаточно так выбрать
поперечные размеры линии, чтобы на любой
частоте рабочего диапазона длина волны
электромагнитных колебаний не превышала
критической длины волны основной волны
.
Для этого достаточно так выбрать
поперечные размеры линии, чтобы на любой
частоте рабочего диапазона длина волны
электромагнитных колебаний не превышала
критической длины волны основной волны![]() ,
но была больше критической длины волны
первого высшего типа
,
но была больше критической длины волны
первого высшего типа![]() .
Первым высшим типом называют волну,
критическая длина которой меньше
.
Первым высшим типом называют волну,
критическая длина которой меньше![]() основной волны, но больше критических
длин волн всех остальных типов волн.
Такой режим передачи энергии называют
одноволновым. Полосу частот, в пределах
которой сохраняется одноволновый режим,
обычно характеризуют коэффициентом
широкополосности
основной волны, но больше критических
длин волн всех остальных типов волн.
Такой режим передачи энергии называют
одноволновым. Полосу частот, в пределах
которой сохраняется одноволновый режим,
обычно характеризуют коэффициентом
широкополосности
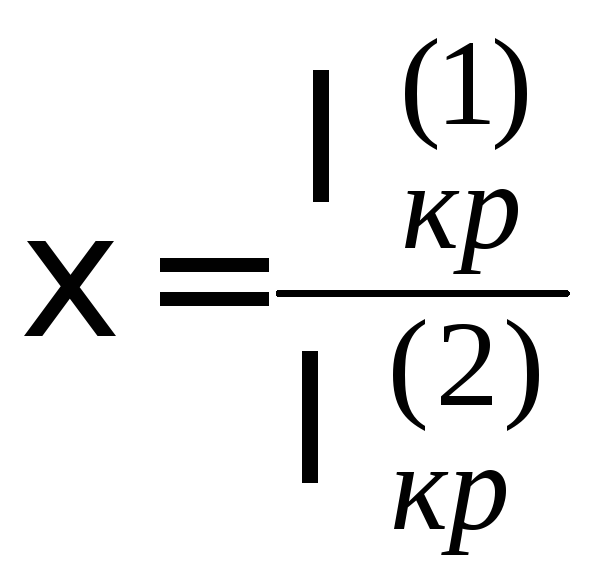 .
.
Основная волна прямоугольного волновода
−
![]() ,
ее
,
ее![]() .
Распространение этой волны возможно
при
.
Распространение этой волны возможно
при![]() или
или![]() .
Чтобы другие типы волн не могли
распространяться, достаточно потребовать,
чтобы не могли распространяться волны
.
Чтобы другие типы волн не могли
распространяться, достаточно потребовать,
чтобы не могли распространяться волны![]() и
и![]() .
Для этого должны выполняться равенства
.
Для этого должны выполняться равенства![]() и
и![]() ,
т.е.
,
т.е.![]() и
и![]() .
Таким образом, одноволновый режим в
прямоугольном волноводе выполняется
при
.
Таким образом, одноволновый режим в
прямоугольном волноводе выполняется
при
![]() и
и![]() .
.
Обычно принимают
![]() и
и![]() ,
где
,
где![]() −средняя длина волны рабочего диапазона.
Для такого волновода коэффициент
широкополосности
−средняя длина волны рабочего диапазона.
Для такого волновода коэффициент
широкополосности .
Для обеспечения одноволнового режима
во всем используемом диапазоне длин
волн
.
Для обеспечения одноволнового режима
во всем используемом диапазоне длин
волн![]() необходимо, чтобы выполнялись равенства
необходимо, чтобы выполнялись равенства![]() и
и![]() .
.
Волноводы п- и н-образной формы
Одноволновый режим в стандартном прямоугольном волноводе, как было показано ранее, сохраняется в двукратной полосе частот. Однако используемый на практике диапазон частот обычно не превышает полуторакратного, поскольку в области частот, близких к критической, велики тепловые потери и мала допустимая мощность.
В значительно большей полосе частот
можно сохранить одноволновый режим при
использовании П- и Н-образных волноводов,
которые часто называют более коротко
просто П- и Н-волновод. Если так подобрать
поперечные размеры этих волноводов,
чтобы коэффициент их широкополосности
был равен коэффициенту широкополосности
прямоугольного волновода, то П- и
Н-волноводы будут иметь меньшие габариты,
чем прямоугольный волновод. На рисунке
Рисунок 26 показана структура электрического
поля соответственно волн
![]() и
и![]() в поперечном сечении П-волновода. Эти
волны названы
в поперечном сечении П-волновода. Эти
волны названы![]() и
и![]() условно. Основанием для этого является
то, что при плавном уменьшении высоты
прямоугольного выступа
условно. Основанием для этого является
то, что при плавном уменьшении высоты
прямоугольного выступа![]() (обычно его называют ребром) они постепенно
преобразуются в волны
(обычно его называют ребром) они постепенно
преобразуются в волны![]() и
и![]() прямоугольного волновода.
прямоугольного волновода.
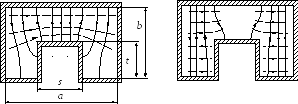
−П-образный волновод
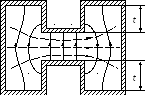
− Н-образный волновод
При равных размерах
![]() и
и![]() расширение рабочей полосы частот у Н-
и П-волноводов по сравнению с прямоугольным
достигается за счет того, что они имеют
практически равные критические частоты
для волны
расширение рабочей полосы частот у Н-
и П-волноводов по сравнению с прямоугольным
достигается за счет того, что они имеют
практически равные критические частоты
для волны![]() ,
а критическая частота для волны
,
а критическая частота для волны![]() в Н- и П-волноводах существенно ниже,
чем в прямоугольных. Сказанное можно
объяснить следующим образом. Ребро (или
ребра у Н-волновода) находится в пучности
напряженности электрического поля
волны
в Н- и П-волноводах существенно ниже,
чем в прямоугольных. Сказанное можно
объяснить следующим образом. Ребро (или
ребра у Н-волновода) находится в пучности
напряженности электрического поля
волны![]() ,
где концентрация электромагнитного
поля относительно велика. Наличие ребра
приводит к еще большей концентрации
поля и энергии в этом месте. Поэтому
свойства волны и, в частности, критическая
частота, определяются в основном
структурой поля в зазоре. Пока отношение
ширины ребра
,
где концентрация электромагнитного
поля относительно велика. Наличие ребра
приводит к еще большей концентрации
поля и энергии в этом месте. Поэтому
свойства волны и, в частности, критическая
частота, определяются в основном
структурой поля в зазоре. Пока отношение
ширины ребра![]() к ширине волновода
к ширине волновода![]() не превышает
не превышает![]() ,
энергия электрического и магнитного
полей вблизи боковых стенок волновода
мала и мала продольная составляющая
,
энергия электрического и магнитного
полей вблизи боковых стенок волновода
мала и мала продольная составляющая![]() магнитного поля. Распространяющаяся в
П-волноводе волна близка по структуре
к ТЕМ-волне. Поэтому введение ребра
приближает структуру волны
магнитного поля. Распространяющаяся в
П-волноводе волна близка по структуре
к ТЕМ-волне. Поэтому введение ребра
приближает структуру волны![]() к структуре ТЕМ-волны и приводит к
понижению критической частоты волны
к структуре ТЕМ-волны и приводит к
понижению критической частоты волны![]() .
Напомним, что у ТЕМ-волны
.
Напомним, что у ТЕМ-волны![]() .
.
Чем больше высота
![]() ребра, т.е., чем ближе отношение
ребра, т.е., чем ближе отношение![]() к единице, тем выше концентрация поля
в зазоер и тем, следовательно, ниже
критическая частота волны
к единице, тем выше концентрация поля
в зазоер и тем, следовательно, ниже
критическая частота волны![]() .
В то же время влияние относительно
узкого (
.
В то же время влияние относительно
узкого (![]() )
ребра (или ребер в Н-волноводе) на
критическую частоту волны
)
ребра (или ребер в Н-волноводе) на
критическую частоту волны![]() незначительно, так как ребро вводится
в сечение, где напряженность электрического
поля волны
незначительно, так как ребро вводится
в сечение, где напряженность электрического
поля волны![]() мала. Поэтому при
мала. Поэтому при![]() коэффициент широкополосности
коэффициент широкополосности![]() Н- и П-образного волновода существенно
выше, чем прямоугольного волновода с
теми же размерами
Н- и П-образного волновода существенно
выше, чем прямоугольного волновода с
теми же размерами![]() и
и![]() .
Дальнейшее увеличение отношения
.
Дальнейшее увеличение отношения![]() приводит к уменьшению коэффициента
широкополосности, так как боковые стенки
волновода приближаются к краям ребер,
возрастает концентрация энергии полей
вблизи боковых стенок и увеличивается
продольная составляющая
приводит к уменьшению коэффициента
широкополосности, так как боковые стенки
волновода приближаются к краям ребер,
возрастает концентрация энергии полей
вблизи боковых стенок и увеличивается
продольная составляющая![]() напряженности магнитного поля, повышается
критическая частота волны
напряженности магнитного поля, повышается
критическая частота волны![]() ,
уменьшается коэффициент широкополосности.
,
уменьшается коэффициент широкополосности.
Недостатком П- и Н-волноводов является
повышенный по сравнению с прямоугольным
волноводом уровень потерь и пониженная
электрическая прочность. Чем больше
высота ребра
![]() ,
тем меньше предельная мощность и выше
потери. Поэтому обычно применяют Н- и
П-волноводы с
,
тем меньше предельная мощность и выше
потери. Поэтому обычно применяют Н- и
П-волноводы с![]() .
.
