
сборник НПК 2013
.pdf
материалы XVI научно-практической конференции Научного Общества Учащихся МБОУ гимназии №6 г.Воронежа
ОРИОН - одно из наиболее красивых созвездий на небосклоне. Оно находится высоко над горизонтом и лучше всего наблюдается по ночам с декабря по март.40 Это созвездие привлекает внимание наблюдателей не только яркостью звезд, но и огромной видимой площадью, которую оно занимает. Вокруг Ориона находятся созвездия Близнецов, Единорога, Эридана и Тельца.
Вясную и безлунную ночь в Орионе можно различить невооруженным глазом до 120 звезд. Самые яркие из них - красноватая Бетельгейзе и бело-голубой Ригель (обе нулевой звездной величины). Вместе с еще двумя звездами второй величины они образуют характерную геометрическую фигуру созвездия Ориона - большой удлиненный неправильный четырехугольник. Посредине его под небольшим наклоном расположены еще три звезды второй звездной величины, образующие "пояс" Ориона. Кроме упомянутых, в созвездии Ориона есть еще десять звезд ярче четвертой звездной величины. Однако необходимо большое усилие воображения, чтобы в этой конфигурации звезд увидеть легендарного охотника Ориона, высоко поднявшего правой рукой огромную дубину, с переброшенной через левую руку львиной шкурой. На правом плече Ориона находится звезда Бетельгейзе, а в ступне левой ноги - звезда Ригель.Звезда Ориона блестит аа его искривленном мече, а в дубине сверкает κ Ориона. Десяток слабых беспорядочно разбросанных звезд напоминают львиную шкуру, которую Орион перебросил через вытянутую левую руку.
Всозвездии Ориона самое сильное впечатление производит звезда Бетельгейзе (α Ориона), имеющая красноватый цвет. Это сверхгигант, ее диаметр в 400 раз больше диаметра Солнца. Если
вцентре этой звезды поместить Солнце, то в ней еще могли бы разместиться м орбиты планет, включая Марс. Расстояние от нас до этой звезды-сверхгиганта - 650 световых лет.
Геометрия - это таинственная страна, где живут точки, прямые линии, прямоугольники, квадраты и еще много - много других фигур.
В этой стране случаются разные забавные истории, и одну из них мы вам сейчас расскажем…
Прямоугольник все время завидовал Квадрату.
–Я такой неуклюжий, – жаловался он. – Если поднимусь во весь рост, то стану длинным и узким. А если лягу на бок, то буду низким и толстым.
–А ты всегда остаешься одинаковым, – продолжал он, обращаясь к Квадрату. – И стоя, и сидя, и лежа!
–Да уж, – с гордостью говорил важный Квадрат. – У меня все стороны равны. Не то, что у некоторых: то дылда-дылдой, а то блин-блином.
141
материалы XVI научно-практической конференции Научного Общества Учащихся МБОУ гимназии №6 г.Воронежа
И Квадрат переворачивался с боку на бок, но его рост и ширина от этого не менялись.
Аоднажды случилось вот что. Один Человек заблудился в лесу. Он шел наугад сквозь чащу и встретился с Квадратом и Прямоугольником. Поскольку у Квадрата был очень важный вид, то Человек обратился за помощью именно к нему.
– Можно, я заберусь на вас и погляжу, где мой дом? – спросил он у Квадрата.
Человек залез сначала на одну сторону Квадрата. Но ничего не увидел, потому что ему мешали макушки деревьев.
Тогда Человек попросил Квадрат перевернуться и залез на другую сторону. Но, как известно, все стороны у Квадрата одинаковые. Поэтому и на сей раз Человек ничего не увидел изза деревьев.
– Гражданин Квадрат! – взмолился Человек. – Помогите мне хотя бы через речку перебраться!
Квадрат подошел к речке и попытался дотянуться до другого берега. Но... плюх! Плюхнулся в воду.
– Может, я смогу помочь вам? – предложил Человеку скромный Прямоугольник. Он встал во весь свой рост. Человек забрался на него и оказался выше деревьев.
Вдалеке он увидел свой дом и наконец понял, куда ему надо идти. Тогда Прямоугольник лег на бок и стал мостом.
Человек перебрался по Прямоугольнику через речку, помог ему подняться и, горячо поблагодарив, отправился домой.
АКвадрат, который сушился на берегу после вынужденного купания, сказал Прямоугольнику:
– Вы, оказывается, полезная фигура!
– Ну, что вы! – скромно улыбнулся Прямоугольник. – Просто мои стороны разной длины: две – длинные, а две – короткие. Иногда это бывает очень удобно.
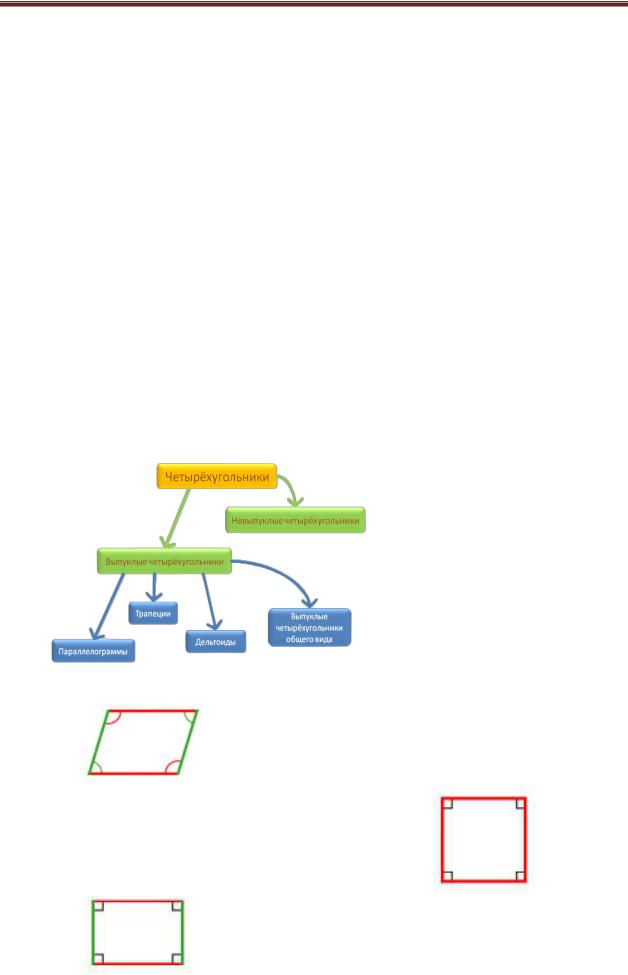
Выпуклые четырехугольники - Это фигура, в которой отрезок соединяющий любые две точки не выходит за пределы этой фигуры.
Параллелограмм — четырехугольник, у которого противоположные стороны попарн6о параллельны
Квадрат - четырѐхугольник, у которого все углы прямые и все стороны равны.
Прямоугольник - четырѐхугольник, у которого все углы прямые и все стороны равны
142
материалы XVI научно-практической конференции Научного Общества Учащихся МБОУ гимназии №6 г.Воронежа
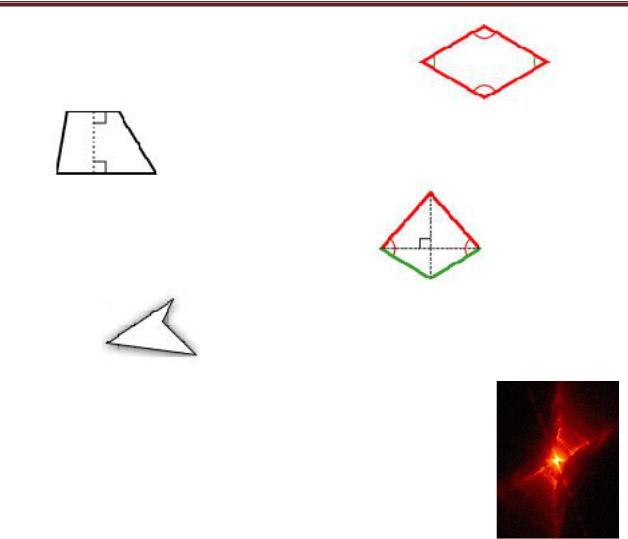
Ромб — четырѐхугольник, у которого все стороны равны
Трапеция — четырѐхугольник, у которого две противоположные стороны параллельны
Ромбоид (дельтоид) — это параллелограмм, в котором смежные стороны имеют разные длины, и углы не являются прямыми.
Не выпуклые четырехугольники. Четырѐхугольник называется не выпуклым, если он не лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины
Туманность Красный прямоугольник— протопланетарная туманность в созвездии Единорога на расстоянии 2 300 световых лет от Земли, названная так из-за своего красного цвета и уникальной прямоугольной формы. Туманность была обнаружена в 1973 году во время полета ракеты.
Загадки:
А братишка мой, Серѐжа, Математик и чертѐжникНа столе у бабы Шуры Чертит всякие….(фигуры)
Не овал я и не круг, Треугольнику я друг, Прямоугольнику я брат, Ведь зовут меня...(квадрат)
Песня о четырехугольниках
Мы сегодня будем изучать Четырехугольные фигуры: Параллелограммы, ромб, квадрат, Трапеции и прямоугольник.
Припев:
Ине можем мы поделать ничего. Напрасно геометрию ругая, ругая Понемногу все мы узнаем
Иво всем друг другу помогаем
143
материалы XVI научно-практической конференции Научного Общества Учащихся МБОУ гимназии №6 г.Воронежа
СПИСОК ЛИТЕРАТУРЫ:
1.Учебник по геометрии 7-9 класс, Атанасян Л.С.
2.Учебник по геометрии 7-9 класс, Погорелов А.В
3.Сайт http://ru.wikipedia.org/wiki/Прямоугольник
КОМПЛЕКСНЫЕ ЧИСЛА (СУМБАР КСЕНИЯ)
Сумбар Ксения, 8А класс учитель Виденькина В.А.
Комплексные числа.
Решение многих задач физики и техники приводит к квадратным уравнениям с отрицательным дискриминантом. Эти уравнения не имеют решения в области действительных чисел. Но решение многих таких задач имеет вполне определенный физический смысл. Значение величин, получающихся в результате решения указанных уравнений, назвали комплексными числами. Комплексные числа широко использовал отец русской авиации Н. Е. Жуковский (1847 – 1921) при разработке теории крыла, автором которой он является. Комплексные числа и функции от комплексного переменного находят применение во многих вопросах науки и техники.
Комплексные числа — расширение поля вещественных чисел, обычно обозначается  .
.
Любое комплексное число может быть представлено как формальная сумма  , где
, где  и
и
— вещественные числа,  — мнимая единица.
— мнимая единица.
Вещественное, или действительное число — математическая абстракция, возникшая из потребности измерения геометрических и физических величин окружающего мира, а также проведения таких операций как извлечение корня, вычисление логарифмов, решение алгебраических уравнений.
2. Исторические сведения.
Квадратные уравнения умели решать еще вавилоняне. Это было связано с решением задач о нахождении площадей земельных участков, а также с развитием астрономии.
Однако у вавилонян еще не было понятия отрицательного числа, и поэтому корни квадратного уравнения могли быть только положительными.
Только в XVI веке благодаря исследованиям французского математика Ф. Виета впервые уравнения 2-й степени, так же, впрочем, как 3-й и 4-й степени, стали рассматривать в буквенных обозначениях. Однако сам Виет признавал только положительные корни.
Лишь в XVII веке после работ Декарта, Ньютона и других математиков решение квадратных уравнений приняло современный вид.
Уже в древности математики сталкивались в процессе решения задач с извлечением квадратного корня из отрицательного числа, в этом случае задача считалась неразрешимой. Однако постепенно выяснилось, что решение многих задач, задаваемых в действительных числах, получает простое объяснение при помощи выражений a+b*(-1) в квадрате, которые в конце концов тоже стали называть числами, но уже комплексными.
Первое обоснование простейших действий с комплексными числами дал итальянский математик Бомбелли, хотя еще долгое время к комплексным числам относились как к чему-то сверхъестественному. Член Петербургской академии наук Эйлер внес существенный вклад в вопросы теории комплексных чисел. После его работ комплексные числа получили окончательное признание как предмет и средство изучения. Само название «комплексное число» было предложено в 1831 году немецким математиком Карлом Гауссом.
Итак, рассмотрим уравнение
2 − 2 + 2 = 0
Оно имеет отрицательный дискриминант -4, чисто формально напишем формулы для его корней:
+ −1
−
1,2 = 1
До сих пор считалось, что такие выражения не имеют смысла, так как символу −1 не соответствует никакое действительное число. Однако этот символ оказался очень полезным в
математике. Его обозначают буквой : −1 = и называют мнимой единицей.
3.Действия над комплексными числами
144
материалы XVI научно-практической конференции Научного Общества Учащихся МБОУ гимназии №6 г.Воронежа
Сложение комплексных чисел. Суммой двух комплексных чисел 1 = + и 2 = +
называется комплексное = + + + . |
Числа |
+ и |
− |
называются |
сопряженными. Их сумма равна действительному числу 2а + + − |
= 2 . Числа а+bi и - |
|||
a-bi называются противоположными. Их сумма равна нулю. |
Комплексные числа равны, если |
|||
равны их действительные части и коэффициенты мнимых частей: + = + , |
если = , |
|||
= . Комплексное число равно нулю тогда, когда его действительная часть и коэффициент мнимой части равны нулю, т.е. = + = 0, если = 0, = 0. Действительные числа являются
частным случаем комплексных чисел. |
Если = 0, то |
+ = - действительное |
число. Если |
= 0, = 0, то + = – чисто |
мнимое число. |
Для комплексных чисел |
справедливы |
переместительный и сочетательный законы сложения. Их справедливость следует из того, что сложение комплексных чисел по существу сводится к сложению действительных частей и
коэффициентов мнимых частей, а они являются |
действительными числами, |
для которых |
справедливы указанные законы. |
|
|
Вычитание комплексных чисел определяется как действие, обратное |
сложению: |
|
разностью двух комплексных чисел + и |
+ называется комплексное |
число + , |
которое в сумме с вычитаемым дает уменьшаемое. Отсюда, исходя из определения сложения и равенства комплексных чисел получим два уравнения, из которых найдем, что = − , = −. Значит, + − + = − + − .
Сравнение
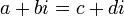 означает, что
означает, что  и
и  (два комплексных числа равны между собой тогда и только тогда, когда равны их действительные и мнимые части).
(два комплексных числа равны между собой тогда и только тогда, когда равны их действительные и мнимые части).
Сложение
Вычитание
Умножение
Деление
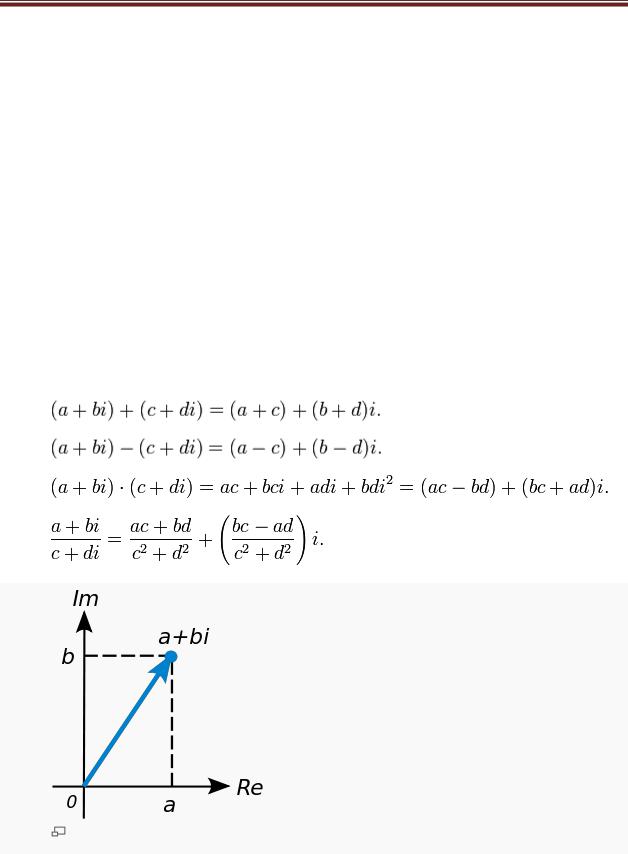
6.Геометрическая модель
Геометрическое представление комплексного числа Рассмотрим плоскость с прямоугольной системой координат. Каждому комплексному
числу  сопоставим точку плоскости с координатами
сопоставим точку плоскости с координатами  (а также радиус-вектор, соединяющий начало координат с этой точкой). Такая плоскость называется комплексной. Вещественные числа на ней занимают горизонтальную ось, мнимая единица изображается единицей на вертикальной оси; по этой причине горизонтальная и вертикальная оси называются соответственно вещественной и мнимой осями.
(а также радиус-вектор, соединяющий начало координат с этой точкой). Такая плоскость называется комплексной. Вещественные числа на ней занимают горизонтальную ось, мнимая единица изображается единицей на вертикальной оси; по этой причине горизонтальная и вертикальная оси называются соответственно вещественной и мнимой осями.
145
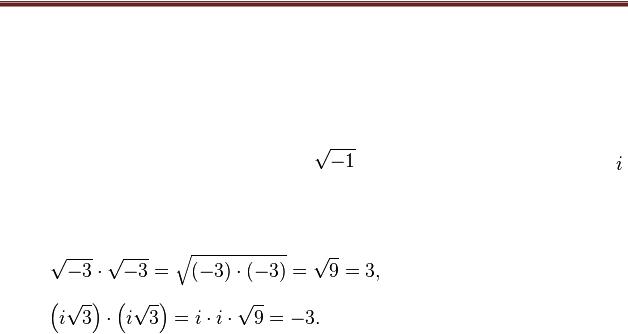
материалы XVI научно-практической конференции Научного Общества Учащихся МБОУ гимназии №6 г.Воронежа
Часто бывает удобно рассматривать на комплексной плоскости также полярную систему координат, в которой координатами точки являются расстояние до начала координат (модуль) и угол радиус-вектора точки (показанного синей стрелкой на рисунке) с горизонтальной осью
(аргумент).
Замечания
Ошибочно определение числа  как единственного числа, удовлетворяющего уравнению
как единственного числа, удовлетворяющего уравнению  , так как число
, так как число 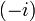 также удовлетворяет этому уравнению.
также удовлетворяет этому уравнению.
Следует также заметить, что выражение |
, ранее часто использовавшееся вместо , |
не вполне корректно, так как алгебраический |
корень определяется над множеством |
неотрицательных чисел. Вплоть до конца XIX века запись вроде  считалась допустимой, но в настоящее время, во избежание ошибок, принято записывать это выражение как
считалась допустимой, но в настоящее время, во избежание ошибок, принято записывать это выражение как
 . Пример возможной ошибки при неосторожном использовании устаревшей записи:
. Пример возможной ошибки при неосторожном использовании устаревшей записи:
в то время как правильная запись приводит к иному ответу:
СПИСОК ЛИТЕРАТУРЫ:
1.http://ru.wikipedia.org/wiki/
2.С.М. Никольский, М.К. Потапов, Н.Н.Решетников, А.В. Шевкин. Учебник 8 класса по алгебре – М.: Просвещение, 2010. С. 118 - 122
КОМПЬЮТЕРНАЯ ГРАФИКА (СУМБАР, ЛАНКИНА)
Сумбар Ксения, Ланкина Мария, 8а класс учитель Муратов М.А.
Компьютерная графика (также машинная графика) — область деятельности, в которой компьютеры используются в качестве инструмента как для создания изображений, так и для обработки визуальной информации, полученной из реального мира.
Первые вычислительные машины не имели отдельных средств для работы с графикой, однако уже использовались для получения и обработки изображений. Программируя память первых электронных машин, построенную на основе матрицы ламп, можно было получать узоры.
В1961 году программист С. Рассел возглавил проект по созданию первой компьютерной игры с графикой. Создание игры («spacewar!») заняло около 200 человеко-часов. Игра была создана на машине PDP-1.
В1963 году американский учѐный Айвен Сазерленд создал программно-аппаратный комплекс Sketchpad, который позволял рисовать точки, линии и окружности на трубке цифровым пером. Поддерживались базовые действия с примитивами: перемещение, копирование и др. По сути, это был первый векторный редактор, реализованный на компьютере. Также программу можно назвать первым графическим интерфейсом, причѐм она являлась таковой ещѐ до появления самого термина.
Всередине 1960-х гг. появились разработки в промышленных приложениях компьютерной графики. Так, под руководством Т. Мофетта и Н. Тейлора фирма Itek разработала цифровую электронную чертѐжную машину. В 1964 году General Motors представила систему автоматизированного проектирования DAC-1, разработанную совместно с IBM.
В1964 году группой под руководством Н.Н. Константинова была создана компьютерная математическая модель движения кошки. Машина БЭСМ-4, выполняя написанную программу решения дифференциальных уравнений, рисовала мультфильм «Кошечка», который для своего времени являлся прорывом. Для визуализации использовался алфавитно-цифровой принтер.
В1968 году cущественный прогресс компьютерная графика испытала с появлением возможности запоминать изображения и выводить их на компьютерном дисплее, электроннолучевой трубке.
Существуют по крайней мере четыре вида компьютерной графики:
1.Векторная графика.
146

материалы XVI научно-практической конференции Научного Общества Учащихся МБОУ гимназии №6 г.Воронежа
2.Растровая графика.
3.Фрактальная графика. 4.Трехмерная графика.
Векторная графика представляет изображение как набор геометрических примитивов.
Обычно в качестве них выбираются точки, прямые, окружности, прямоугольники, а также как общий случай, кривые некоторого порядка. Объектам присваиваются некоторые атрибуты, например, толщина линий, цвет заполнения. Рисунок хранится как набор координат, векторов и других чисел, характеризующих набор примитивов. При воспроизведении перекрывающихся объектов имеет значение их порядок.
Изображение в векторном формате даѐт простор для редактирования. Изображение может без потерь масштабироваться, поворачиваться, деформироваться, также имитация трѐхмерности в векторной графике проще, чем в растровой. Дело в том, что каждое такое преобразование фактически выполняется так: старое изображение (или фрагмент) стирается, и вместо него строится новое. Математическое описание векторного рисунка остаѐтся прежним, изменяются только значения некоторых переменных, например, коэффициентов. При преобразовании растровой картинки исходными данными является только описание набора пикселей, поэтому возникает проблема замены меньшего числа пикселей на большее (при увеличении), или большего на меньшее (при уменьшении). Простейшим способом является замена одного пикселя несколькими того же цвета (метод копирования ближайшего пикселя: Nearest Neighbour). Более совершенные методы используют алгоритмы интерполяции, при которых новые пиксели получают некоторый цвет, код которого вычисляется на основе кодов цветов соседних пикселей. Подобным образом выполняется масштабирование в программе Adobe Photoshop.
Вместе с тем, не всякое изображение можно представить как набор из примитивов. Такой способ представления хорош для схем, используется для масштабируемых шрифтов, деловой графики, очень широко используется для создания мультфильмов и просто роликов разного содержания.
Растровая графика всегда оперирует двумерным массивом (матрицей) пикселей. Каждому пикселю сопоставляется значение — яркости, цвета, прозрачности — или комбинация этих значений. Растровый образ имеет некоторое число строк и столбцов.
Без особых потерь растровые изображения можно только лишь уменьшать, хотя некоторые детали изображения тогда исчезнут навсегда, что иначе в векторном представлении. Увеличение же растровых изображений оборачивается «красивым» видом на увеличенные квадраты того или иного цвета, которые раньше были пикселями.
Врастровом виде представимо любое изображение, однако этот способ хранения имеет свои недостатки: больший объѐм памяти, необходимый для работы с изображениями, потери при редактировании.
Фрактальная графика.
Фрактал — объект, отдельные элементы которого наследуют свойства родительских структур. Поскольку более детальное описание элементов меньшего масштаба происходит по простому алгоритму, описать такой объект можно всего лишь несколькими математическими уравнениями.
Фракталы позволяют описывать целые классы изображений, для детального описания которых требуется относительно мало памяти. С другой стороны, фракталы слабо применимы к изображениям вне этих классов.
Трехмерная графика (3D — от англ. three dimensions — «три измерения») оперирует с объектами в трѐхмерном пространстве. Обычно результаты представляют собой плоскую картинку, проекцию. Трѐхмерная компьютерная графика широко используется в кино, компьютерных играх.
Втрѐхмерной компьютерной графике все объекты обычно представляются как набор поверхностей или частиц. Минимальную поверхность называют полигоном. В качестве полигона обычно выбирают треугольники.
Всеми визуальными преобразованиями в 3D-графике управляют матрицы. В компьютерной графике используется три вида матриц:
Матрица поворотаматрица сдвига
матрица масштабирования
147
материалы XVI научно-практической конференции Научного Общества Учащихся МБОУ гимназии №6 г.Воронежа
Любой полигон можно представить в виде набора из координат его вершин. Так, у треугольника будет 3 вершины. Координаты каждой вершины представляют собой вектор (x, y, z). Умножив вектор на соответствующую матрицу, мы получим новый вектор. Сделав такое преобразование со всеми вершинами полигона, получим новый полигон, а преобразовав все полигоны, получим новый объект, повѐрнутый/сдвинутый/масштабированный относительно исходного.
Реальная сторона графики
Любое изображение на мониторе, в силу его плоскости, становится растровым, так как монитор это матрица, он состоит из столбцов и строк. Трѐхмерная графика существует лишь в нашем воображении, так как то, что мы видим на мониторе — это проекция трѐхмерной фигуры, а уже создаѐм пространство мы сами. Таким образом, визуализация графики бывает только растровая и векторная, а способ визуализации это только растр (набор пикселей), а от количества этих пикселей зависит способ задания изображения.
ПРИМЕНЕНИЕ ФОРМУЛЫ ПИКА (СУХАНОВА ЮЛИЯ)
Суханова Юлия, 5А класс учитель Охотенко Н.Н.
Рассмотрим невырожденный простой целочисленный многоугольник (т.е. он связный — любые две его точки могут быть соединены непрерывной кривой, целиком в нем содержащейся, и все его вершины имеют целые координаты, его граница — связная ломаная без самопересечений, и он имеет ненулевую площадь).
Для вычисления площади такого многоугольника можно воспользоваться следующей теоремой:
Теорема Пика. Пусть  — число целочисленных точек внутри многоугольника,
— число целочисленных точек внутри многоугольника,  — количество целочисленных точек на его границе,
— количество целочисленных точек на его границе,  — его площадь. Тогда справедлива формула Пика:
— его площадь. Тогда справедлива формула Пика:
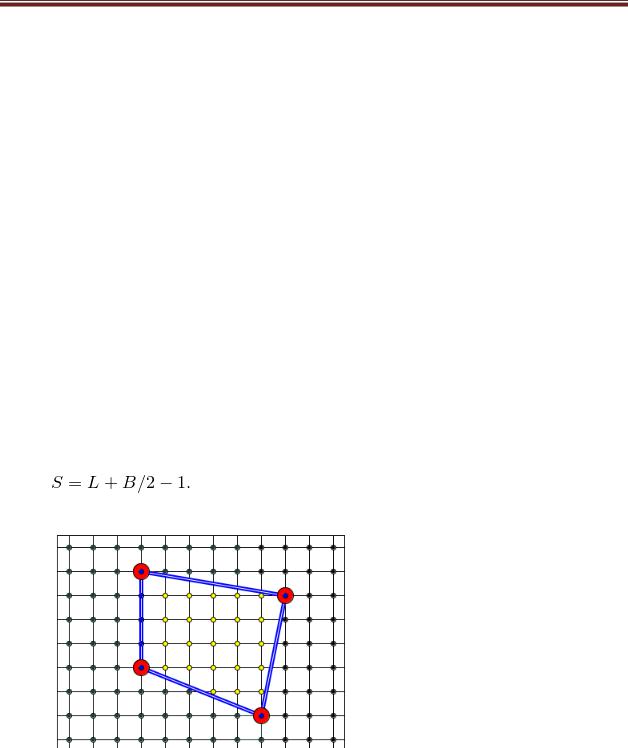
Пример. Для многоугольника на рисунке  (желтые точки),
(желтые точки),  (синие точки, не забудьте о вершинах!), поэтому
(синие точки, не забудьте о вершинах!), поэтому  квадратных единиц.
квадратных единиц.
Доказательство теоремы Пика. Сначала заметим, что формула Пика верна для единичного квадрата. Действительно, в этом случае мы имеем 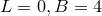 и
и
 .
.
Рассмотрим прямоугольник со сторонами, лежащими на линиях решетки. Пусть длины его сторон равны 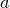 и
и  . Имеем в этом случае
. Имеем в этом случае 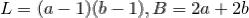 и, по формуле
и, по формуле
Пика,  Рассмотрим теперь прямоугольный треугольник с катетами, лежащими на осях координат.
Рассмотрим теперь прямоугольный треугольник с катетами, лежащими на осях координат.
Такой треугольник получается из прямоугольника со сторонами  и
и  , рассмотренного в предыдущем случае, разрезанием его по диагонали. Пусть на диагонали лежат
, рассмотренного в предыдущем случае, разрезанием его по диагонали. Пусть на диагонали лежат  целочисленных
целочисленных
148
материалы XVI научно-практической конференции Научного Общества Учащихся МБОУ гимназии №6 г.Воронежа
точек. Тогда для этого случая |
и |
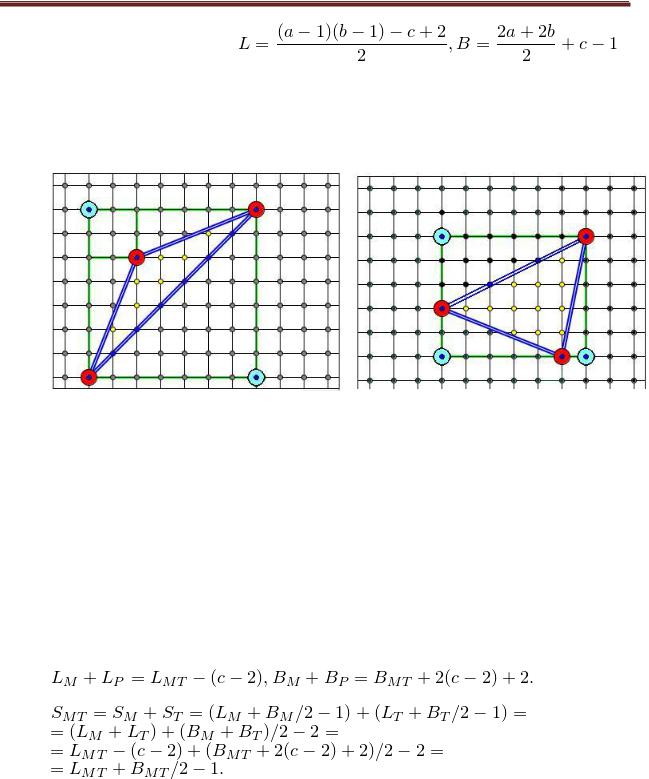
получаем, что  Теперь рассмотрим произвольный треугольник. Его можно получить, отрезав от
Теперь рассмотрим произвольный треугольник. Его можно получить, отрезав от
прямоугольника несколько прямоугольных треугольников и, возможно, прямоугольник (см. рисунки). Поскольку и для прямоугольника, и для прямоугольного треугольника формула Пика верна, мы получаем, что она будет справедлива и для произвольного треугольника.
Остается сделать последний шаг: перейти от треугольников к многоугольникам. Любой многоугольник можно разбить на треугольники (например, диагоналями). Поэтому нужно просто доказать, что при добавлении любого треугольника к произвольному многоугольнику формула Пика остается верной.
Пусть многоугольник  и треугольник
и треугольник  имеют общую сторону. Предположим, что для
имеют общую сторону. Предположим, что для  формула Пика справедлива, докажем, что она будет верна и для многоугольника, полученного из
формула Пика справедлива, докажем, что она будет верна и для многоугольника, полученного из  добавлением
добавлением 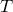 . Так как
. Так как  и
и 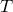 имеют общую сторону, то все целочисленные точки, лежащие на этой стороне, кроме двух вершин, становятся внутренними точками нового многоугольника. Вершины же будут граничными точками. Обозначим число общих точек через
имеют общую сторону, то все целочисленные точки, лежащие на этой стороне, кроме двух вершин, становятся внутренними точками нового многоугольника. Вершины же будут граничными точками. Обозначим число общих точек через  и получим
и получим
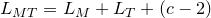 — число внутренних целочисленных точек нового многоугольника,
— число внутренних целочисленных точек нового многоугольника,
 — число граничных точек нового многоугольника.
— число граничных точек нового многоугольника.
Из этих равенств получаем
Так как мы предположили, что теорема верна для  и для
и для  по отдельности, то
по отдельности, то
Тем самым, формула Пика доказана.
Рассмотрим каким образом формула Пика применяется для нахождения площади многоугольника изображенного на клетчатой бумаге
149

материалы XVI научно-практической конференции Научного Общества Учащихся МБОУ гимназии №6 г.Воронежа
СЕКЦИЯ «ЕСТЕСТВЕННО-НАУЧНЫЕ ДИСЦИПЛИНЫ» (БИОЛОГИЯ, ХИМИЯ, ФИЗИКА, ГЕОГРАФИЯ)
ЭТИМОЛОГИЯ ТОПОНИМИЧЕСКИХ НАЗВАНИЙ ВОРОНЕЖСКОЙОБЛАСТИ (ГЛАЗКОВА)
Глазкова Александра, 9а класс Учитель Чердынцева Р.Ю.
Я считаю, каждый человек должен знать историю не только своей страны, но и своей области. Ведь область - это твоя «малая» родина. Вот и мне захотелось узнать как можно больше о ней.
Обращение к топонимическим преданиям позволило мне заглянуть в далекое прошлое, когда наша воронежская земля заселялась казаками, защитниками южных рубежей России. В степи распахивались земли, возникали сѐла, строились дома переселенцев-крестьян из центральных и северных губерний России. Из рассказов сельчан об истории родных мест я смогла узнать и о более древних временах: о временах набегов татарских орд, восстания Стеньки Разина, строительства Петром I Российского флота и других исторических событий нашей страны. Русские крестьяне жили в окружении природы и часто давали названия по особенностям ландшафта, по своеобразию расположения рек, лесов, оврагов. Эти и многие другие способы происхождения названий будут описаны ниже.
Все географические названия имеют свой смысл. Никакой народ не называл реку, озеро или селение «просто так», случайным сочетанием звуков. И нет ни одного имени, за которым не стояла бы сложная и загадочная его история... В названиях сохранилась информация давно ушедших времен и память о событиях недавнего прошлого. Отсюда делаем вывод: объяснить можно любое, даже самое сложное и, на первый взгляд, непонятное географическое название.
Цель работы: собрать и изучить топонимы Воронежской области и подготовить материал для создания топонимического словаря.
Объектом исследования являются названия географических объектов и природных ландшафтов Воронежской области.
Предмет исследования – лингвистические особенности топонимов. Соответственно цели выделены следующие задачи исследования:
Изучение литературы по данной теме.
Сбор топонимического материала.
Классификация топонимов Воронежской области.
В работе использованы следующие методы: теоретический анализ, беседа, поиск.
Глава I. Формирование понятий об ономастике и топонимике
Наука, изучающая имена собственные всех типов и их происхождение, называется ономастикой. Это раздел лингвистики, изучающий собственные имена, историю их возникновения и преобразования в результате длительного употребления в языке-источнике или в связи с заимствованием у других языков общения.
Существует несколько направлений ономастики:
Антропонимика исследует собственные имена людей.
Этнонимика изучает названия народов и племѐн.
Космонимика анализирует наименования зон космического пространства – созвездий, галактик, как принятые в науке, так и народные.
Астронимика изучает названия космических объектов, или отдельных небесных светил.
Зоонимика занимается собственными именами животных и их кличками.
Хрематонимика исследует собственные имена предметов материальной культуры.
Теонимика анализирует собственные имена богов и божеств любого пантеона.
Карабонимика изучает собственные имена кораблей, судов и катеров.
Эргонимика занимается наименованиями деловых объединений людей. Например, эмпоронимы – названия магазинов, фирмонимы – названия фирм.
Прагматонимика исследует наименования товаров и других результатов практической деятельности людей. Например, парфюмонимы – названия парфюмерной продукции, ароматов, чоконимы – названия шоколадной продукции.
Топонимика изучает собственные имена географических объектов.
150
