Контрольная работа № 1

Механика

Основные формулы

Кинематика

1. Средняя скорость и среднее ускорение материальной точки

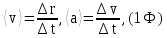
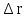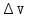
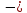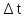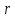
где ,перемещение точки и приращение скорости за время; 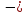радиус-вектор точки. Используется также средняя скорость, равная отношению пройденного пути s ко времени t, за которое этот путь был пройден

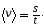(2Ф)

2. Модули скорости и ускорения

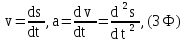
где s – путь, пройденный материальной точкой.

3. Проекции скорости и ускорения на координатные оси

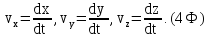
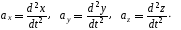(5Ф)

4. Модули скорости и ускорения через их проекции на координатные оси

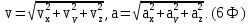
5. Координата точки и проекция скорости на выбранную ось координат при равноускоренном движении

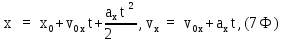
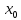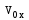
где ,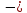начальная координата и проекция начальной скорости.

6. Тангенциальное и нормальное ускорения при криволинейном движении

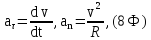
где 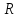– радиус кривизны траектории в данной точке, или радиус окружности.

7. Модули угловой скорости и углового ускорения точки, движущейся по окружности,

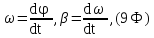
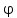
где 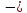угол поворота радиус-вектора точки.

8. Связь между модулями линейных и угловых величин, характеризующих движение точки по окружности,

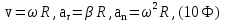
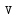
где 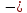линейная скорость;R – радиус окружности.

9. Полное ускорение точки, движущейся по окружности,

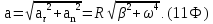
Динамика

10. Второй закон Ньютона

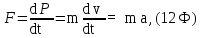
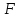
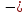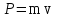
где равнодействующая сила, действующая на тело (материальную точку) массой m; 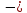импульс тела;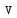 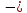его скорость; а – ускорение тела.

11. Третий закон Ньютона

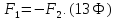
Силы, с которыми взаимодействуют два тела, равны по модулю и противоположны по направлению, имеют одинаковую природу и приложены к разным телам.

12. Силы в механике:

а) гравитационная сила (закон всемирного тяготения)

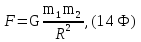
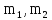
где G – гравитационная постоянная (находится из таблицы); 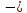массы взаимодействующих тел;R – расстояние между телами (тела рассматриваются как материальные точки или однородные шары);

б) сила упругости (закон Гука)

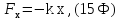
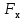
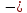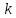
где проекция силы упругости на осьХ; 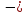коэффициент упругости (жесткость в случае пружины);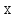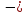проекция перемещения конца пружины или стержня при деформации. Знак «минус» означает, что проекции силы упругости и перемещения конца пружины (стержня) имеют противоположные знаки;

в) сила трения скольжения

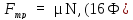
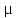
где 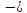коэффициент трения скольжения, зависит от природы и состояния трущихся поверхностей;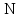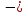сила нормального давления.

Законы сохранения

13. Закон сохранения импульса

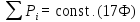
Импульс замкнутой системы тел (или частиц) остается постоянным, т. е. не меняется со временем. Для двух тел (i = 2)

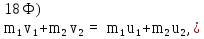
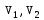
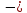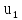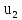
где скорости тел до взаимодействия;,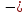скорости тел после взаимодействия.

14. Работа, совершаемая силой F при перемещении частицы из точки 1 в точку 2,

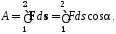(19Ф)

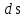
где 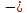элементарное перемещение частицы;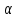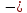угол между перемещением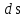и силой.

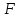15. Кинетическая энергия частицы

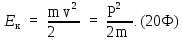
16. Связь кинетической энергии с работой

А = ΔЕ_к = Е_к2 – Е_к1, (21Ф)

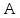
где 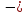работа всех сил, действующих на частицу;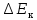 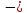приращение кинетической энергии частицы; Е_к1, Е_к2 – кинетическая энергия частицы в моменты времен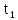и и 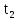. Выражение (21Ф) обобщается на механическую систему: работа всех сил (внутренних и внешних) равна приращению кинетической энергии системы.

17. Потенциальная энергия:

а) упругодеформированной пружины

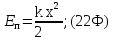
б) тела, находящегося в однородном поле силы тяжести

Е_{п =} mgh, (23Ф)

где h 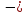высота тела над уровнем, принятым за нулевой. Формула справедлива при h 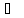R, где R 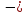радиус Земли.

18. Связь потенциальной энергии с работой консервативных сил

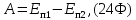
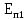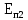
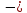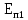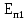где ,потенциальная энергия в точках1 и 2 консервативного поля (например, поля тяжести Земли). Для механической системы под ,следуетпонимать потенциальную энергию системы в двух ее положениях или конфигурациях (начальном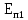и конечном).

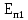19. Закон сохранения энергии

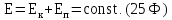
Полная механическая энергия E системы, находящейся под действием консервативных сил, сохраняется с течением времени.