
- •Кафедра оФиФнгп
- •Сборник задач по физике
- •И примеры их решения
- •Часть
- •Предисловие
- •Программа курса физики
- •Молекулярная физика и термодинамика
- •Электростатика
- •Библиографический список
- •Методические указания к решению задач и выполнению контрольных работ
- •Контрольная работа № 1
- •Механика
- •Основные формулы
- •Кинематика
- •Динамика
- •Законы сохранения
- •Динамика твердого тела
- •Механические колебания
- •Примеры решения задач
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •3,8.1016 Дж.
- •Задачи для самостоятельного решения
- •Контрольная работа №2
- •Термодинамика
- •Электростатика
- •Примеры решения задач
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Задачи для самостоятельного решения
- •1. Основные физические константы
- •2. Молярная масса м, 10–3 (кг/моль)
Решение
Воспользуемся
теоремой Карно: коэффициент полезного
действия (к. п. д.)
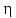 тепловой машины, работающей по циклу
Карно, зависит только от температур
нагревателя
тепловой машины, работающей по циклу
Карно, зависит только от температур
нагревателя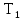 и холодильника
и холодильника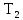 и не зависит от природы рабочего тела
и устройства тепловой машины (см. (16Ф))
и не зависит от природы рабочего тела
и устройства тепловой машины (см. (16Ф))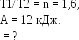

Учитывая условие задачи, получим коэффициент полезного действия машины:
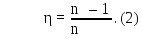
К. п. д. цикла Карно
запишем через работу
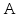 и тепло
и тепло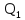 ,
переданное рабочему телу от нагревателя:
,
переданное рабочему телу от нагревателя: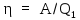 ,
откуда с учетом (2)
,
откуда с учетом (2)
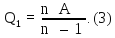
Работа
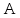 находится через
находится через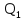 и
тепло
и
тепло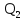 ,
переданное от рабочего тела холодильнику,
,
переданное от рабочего тела холодильнику,
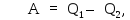
Откуда, учитывая (3), имеем:
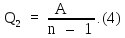
Применим к изотермическому сжатию первое начало термодинамики (9Ф) в виде:

где
Q
–
тепло, переданное рабочему телу. В нашей
задаче Q
=
–
Q2,
т. к. тепло отнимается от тела и
передается холодильнику;
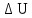 –
приращение внутренней энергии рабочего
тела. У нас
–
приращение внутренней энергии рабочего
тела. У нас
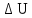 =
0, т. к. Т
=
const
(см. (8Ф));
=
0, т. к. Т
=
const
(см. (8Ф));
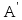 –
искомая работа внешних сил над рабочим
телом. В результате из (5) имеем
–
искомая работа внешних сил над рабочим
телом. В результате из (5) имеем
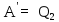 .
Используя (4), найдем:
.
Используя (4), найдем:
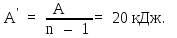
Пример 7. Водород совершает цикл Карно. Найти к. п. д. цикла, если при адиабатическом расширении: а) объем газа увеличивается в n = V2/V1 = 2,0 раза; б) давление уменьшается в n = Р1/Р2 = 2,0 раза.
Решение
а)
Воспользуемся формулой к. п. д. цикла
Карно (16Ф)
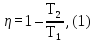
где
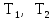 –
температура нагревателя и холодильника.
Используем для адиабатического процесса
уравнение Пуассона (14Ф) в виде:
–
температура нагревателя и холодильника.
Используем для адиабатического процесса
уравнение Пуассона (14Ф) в виде:
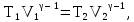
откуда имеем

где
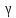 =
1,4 –
постоянная адиабаты для двухатомного
водорода. По условию задачи
=
1,4 –
постоянная адиабаты для двухатомного
водорода. По условию задачи
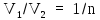 .
Тогда из (2)
.
Тогда из (2)
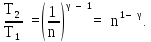
Подставляя это выражение в (1), найдем к. п. д. цикла Карно при увеличении объема газа в n = 2,0 раза
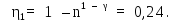
б) Запишем уравнение Пуассона в следующем виде (см. (14Ф)):
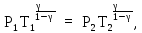
откуда
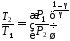 ,
,
или, учитывая условие задачи, получим:
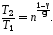
С учетом этого выражения, из (1) найдем к. п. д. цикла, когда давление уменьшается в n = 2,0 раза
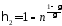
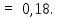
Пример 8.
Один моль гелия при изобарном расширении
увеличил свой объем в
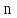 =
V2/V1
=
4,0 раза. Найти приращение энтропии.
=
V2/V1
=
4,0 раза. Найти приращение энтропии.
Решение
Приращение энтропии
находится
из второго
начала термодинамики для равновесных
процессов (17Ф)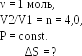
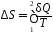 ,(1)
,(1)
где δQ – элементарное количество теплоты, находится из первого начала термодинамики (9Ф), записанного в дифференциальной форме,

Приращение внутренней энергии для одного моля газа (см. (8Ф))

где
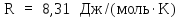 –
универсальная газовая постоянная
(находится из таблицы). Элементарная
работа газа
–
универсальная газовая постоянная
(находится из таблицы). Элементарная
работа газа

Продифференцируем
уравнение состояния идеального газа
(2Ф) для одного моля (ν
=
1) с учетом того, что процесс изобарный:
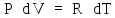 .
Тогда (4) запишется:
.
Тогда (4) запишется:

Подставляя (3) и (5) в уравнение (2), получим:
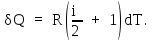
Подставим это выражение в (1) и проинтегрируем:
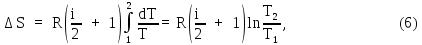
где
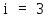 –
число степеней
свободы атомов гелия. Применяя уравнение
Менделеева–Клапейрона
(2Ф) к состояниям газа при изобарном
процессе, получим с учетом условия
задачи:
–
число степеней
свободы атомов гелия. Применяя уравнение
Менделеева–Клапейрона
(2Ф) к состояниям газа при изобарном
процессе, получим с учетом условия
задачи:
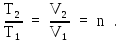
Используя это соотношение, из (6) найдем приращение энтропии:
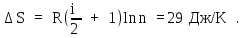
Пример 9.
Один моль двухатомного идеального газа
находится при температуре
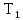 =
300 К и сжимается от объема V1
до объема V2
=
V1/2
один раз изотермически, а другой –
адиабатически. Найти приращение энтропии
и конечную температуру
=
300 К и сжимается от объема V1
до объема V2
=
V1/2
один раз изотермически, а другой –
адиабатически. Найти приращение энтропии
и конечную температуру
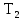 в обоих процессах.
в обоих процессах.
Решение
Для нахождения
приращения энтропии используем второе
начало термодинамики (17Ф)
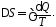 (1)
(1)
Элементарное
количество теплоты
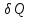 находится из первого начала термодинамики
(9Ф)
находится из первого начала термодинамики
(9Ф)
δQ = dU + δA, (2)
где dU – приращение внутренней энергии. При изотермическом процессе dU = 0 (см. (8Ф)). Элементарная работа газа
δА = PdV . (3)
Из уравнения Менделеева–Клапейрона (2Ф), записанного для одного моля (ν = 1), найдем: P = RT/V, и подставим это выражение в (3). В результате получим
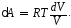 (4)
(4)
Учитывая dU = 0, из (2) и (4) имеем:
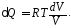
Подставляя это выражение в (1), найдем приращение энтропии при изотермическом сжатии:

Учитывая условие задачи V2 = V1/2 и табличное значение универсальной газовой постоянной R = 8,31 Дж/(моль.К), получим искомое приращение энтропии:
ΔS1
=
–
R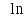 2
=
–
5,76 Дж/К.
2
=
–
5,76 Дж/К.
Знак « минус » означает, что энтропия при этом процессе уменьшается, так как макросистема не является замкнутой.
Для адиабатического
процесса
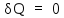 ,
тогда из (1) видно, что
,
тогда из (1) видно, что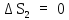 ,
т. е. энтропия при данном процессе
остается постоянной.
,
т. е. энтропия при данном процессе
остается постоянной.
Температура при
изотермическом процессе не изменяется,
следовательно, по условию задачи конечная
температура в этом процессе Т2
=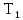 =
300 К. Для адиабатического процесса
используем уравнение Пуассона (14Ф) в
виде:
=
300 К. Для адиабатического процесса
используем уравнение Пуассона (14Ф) в
виде:
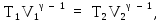 откуда
откуда

Постоянная адиабаты
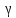 =
CP/СV.
Используя формулы молярных теплоемкостей
CP
и СV
(7Ф), найдем: γ
=
(i
+
2)/i.
В задаче дан двухатомный газ, для которого
число степеней свободы
i
=
5, тогда γ
=
1,4. Учитывая условие задачи V2
=
V1/2,
получим из (5):
=
CP/СV.
Используя формулы молярных теплоемкостей
CP
и СV
(7Ф), найдем: γ
=
(i
+
2)/i.
В задаче дан двухатомный газ, для которого
число степеней свободы
i
=
5, тогда γ
=
1,4. Учитывая условие задачи V2
=
V1/2,
получим из (5):
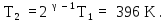
Таким образом, конечная температура больше при адиабатическом сжатии.
Пример 10. Точечные закрепленные заряды q1 = 40 нКл и q2 = – 10 нКл находятся на расстоянии r = 10 cм друг от друга. Где следует поместить третий заряд q3, чтобы он находился в равновесии? При каком знаке заряда q3 равновесие будет устойчивым?
