Lektsia_5_samostoyatelnoe_izuchenie

Лекция 4. Поверхности второго порядка

Цилиндрические поверхности

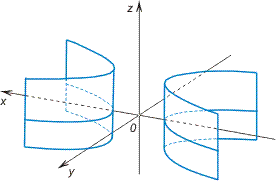
Название цилиндра определяется названием направляющей. Если направляющей служит эллипс

в плоскости , то соответствующая цилиндрическая поверхность назы­вается эллиптическим цилиндром (см. рис. 1).

Рис. 2	Рис. 1

Ч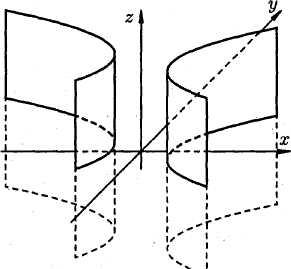астным случаем эллиптического цилиндра является круговой цилиндр, его уравнение . Уравнение

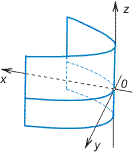
определяет в пространстве параболи­ческий цилиндр (см. рис. 2). Уравнение определяет в пространстве гиперболи­ческий цилиндр

(см. рис. 3).

Все эти поверхности называются цилиндрами второго порядка, так как их уравнения есть уравнения второй степени относительно текущих коорди­нат , и .

Канонические уравнения поверхностей второго порядка

По заданному уравнению поверхности второго порядка (т. е. поверхности, уравнение которой в прямоугольной системе координат является алгебраическим уравнением второй степени) будем определять ее геометрический вид. Для этого применим так называемый метод сечений: исследование вида поверхности будем производить при помощи изучения ли­ний пересечения данной поверхности с координатными плоскостями или плоскостями, им параллельными.

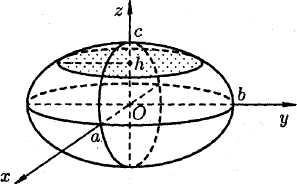
Эллипсоид. Исследуем поверхность, заданную уравнением

. (1)

Рассмотрим сечения поверхности (1) плоскостями, параллельными плоскости . Уравнения таких плоскостей: , где — любое число.

Линия, получаемая в сечении, определяется двумя уравнениями

,

. (2)

Исследуем уравнения (2):

а) Если , , то . Точек пересечения поверхно­сти (1) с плоскостями не существует.

б) Если , т. е. , то . Линия пересечения (2) вырождается в две точки и . Плоскости и касаются данной поверхности.

в) Если , то уравнения (2) можно переписать в виде:

,

.

Как видно, линия пересечения есть эллипс с Рис. 4 полу­осями

и .

При этом чем меньше , тем больше полуоси и . При они достигают своих наибольших значений: , . Уравнения (2) примут вид

,

.

Аналогичные результаты получим, если рассмотрим сечения поверхности (1) плоскостями и .

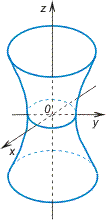
Таким образом, рассмотренные сечения позволяют изобразить поверхность (1) как замкнутую овальную поверхность. Поверхность (1) называется эллипсоидом. Величины a, и называются полуосями эллипсоида. Если все они различны, то эллипсоид называется трехосным; если какие-либо две полуоси равны, трехосный эллипсоид превращается в эллипсоид вращения; если , то – в сферу . Однополостный гиперболоид. Исследуем поверхность, заданную уравнением

. (3)

Анализ этих сечений показывает, что поверхность, определяемая уравнением(3), имеет форму бесконечной расширяющейся трубки см. рис.5.

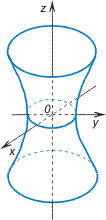
Рис. 5

Двухполостный гиперболоид. Каноническое уравнение имеет вид

₍₄₎

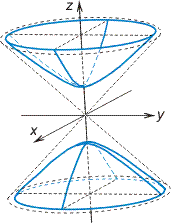
Рис. 6

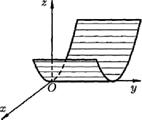
Эллиптический параболоид. Исследуем поверхность, заданную уравнением

, (5)

При пересечении поверхности (5) координатными плоскостями и получатся соответственно параболы и . Таким образом, поверхность, определяемая уравнением (5), имеет вид выпук­лой, бесконечно расширяющейся чаши (см. рис. 7).

Поверхность (5) называется эллиптическим параболоидом.

Гиперболический параболоид. Исследуем поверхность, определяемую уравнением

, (6)

При пересечении поверхности плоскостями, параллельными плоскости ( ), будут получаться параболы

,

,

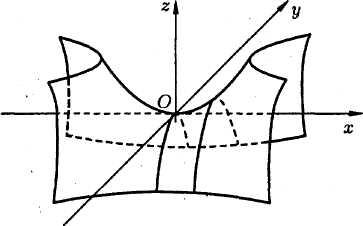
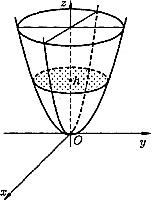
Рис. 8

Рис.7

ветви которых направлены вверх. При в сечении получается парабола

,

с вершиной в начале координат и осью симметрии .

Пересекая поверхность (6) плоскостями , получим параболы , ветви которых направлены вниз.

Анализ линии пересечения позволяет определить вид поверхности: она

имеет вид седла (см. рис. 8). Поверхность (6) называется гиперболическим параболоидом.

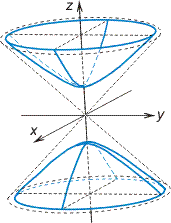
Конус второго порядка. Исследуем уравнение поверхности

. (7)

Пересечем поверхность (7) плоскостями . Линия пересечения , . При она вырождается в точку . При в сечении будем получать эллипсы

.

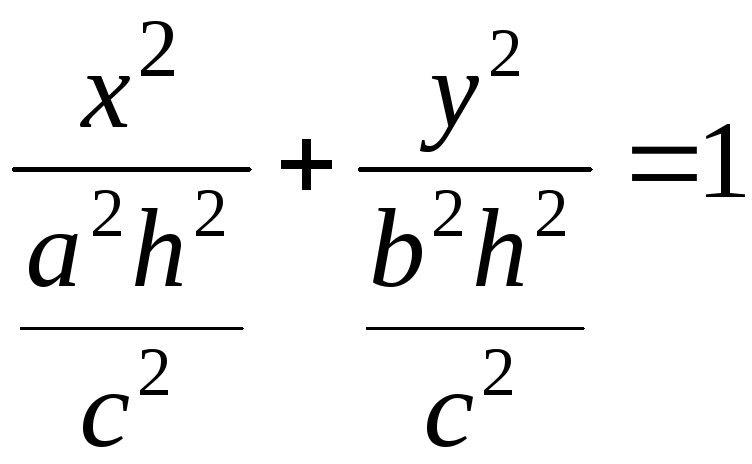
Полуоси этих эллипсов будут возрастать при возрастании .

Поверхность, определяемая уравнени­ем (7), называется конусом второго порядка, имеет вид, изобра­женный на рисунке 9.

Примеры тестовых заданий

1) Поверхность, определяемая уравнением 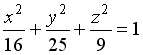, является…

Варианты ответов:

однополостным гиперболоидом; сферой; конусом; эллипсоидом

2) Поверхность, определяемая уравнением , является…

Варианты ответов:

сферой; эллиптическим параболоидом; эллиптическим цилиндром; конусом

3) Поверхность, определяемая уравнением 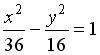, является…

Варианты ответов: эллиптическим цилиндром; гиперболическим цилиндром; конусом; эллипсоидом

4) Поверхность, определяемая уравнением 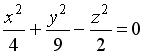, является…

Варианты ответов: эллипсоидом; эллиптическим цилиндром; конусом; сферой

5) Поверхность, определяемая уравнением , является…

Варианты ответов: гиперболическим цилиндром; сферой; конусом; эллиптическим цилиндром

Уравнения поверхностей второго порядка

Эллипсоид a, b, c — полуоси
Однополостный гиперболоид c — действительная полуось, a и b — мнимые полуоси
Двуполостный гиперболоид c — действительная полуось, a и b — мнимые полуоси
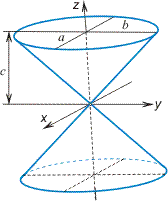
Конус Вершина конуса в начале координат, направляющая кривая — эллипс с полуосями а и b, плоскость которого находится на расстоянии с от начала координат
Эллиптический параболоид
Гиперболический параболоид
Эллиптический цилиндр a и b — полуоси
Гиперболический цилиндр
Параболический цилиндр p — фокальный параметр