ЭМС

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ИНДУСТРИАЛЬНЫЙ УНИВЕРСИТЕТ

В.Н. Чичерюкин

ЭЛЕКТРОМЕХАНИЧЕСКИЕ СИСТЕМЫ

Учебно-методическое пособие

34-54

Москва 2009

ПРЕДИСЛОВИЕ

Пособие написано в соответствии с программой курса «Электромеханические системы» для студентов направления 140500 «Энергомашиностроение» магистратуры МГИУ (9-й семестр). Они могут быть полезны также студентам при изучении дисциплины «Электропневмоавтоматика», а также студентам других направлений обучения.

Материал учебного пособия состоит из восьми глав и методических указаний по курсовому проектированию.

Впервой главе напоминается информация из курса электротехники и электротехнических разделов физики, которая необходима для изучения настоящего курса.

Во второй главе рассматривается обобщённая электромеханическая система, и выявляются электромеханические аналогии.

Втретьей главе анализируется работа основных электромеханических преобразователей.

Четвёртая глава посвящена анализу магнитных полей различных систем с одним или несколькими источниками МДС в виде катушек или постоянных магнитов.

Впятой главе рассмотрены электромагниты постоянного и переменного тока, а также поляризованные электромагниты.

Вшестой главе описаны электромеханические аппараты на магнитоуправляемых контактах.

Вседьмой главе рассмотрены магнитные муфты, опоры и редукторы. Последняя часть с методическими указаниями связана с наличием

курсовой работы в учебном плане дисциплины.

Из-за ограниченного объёма дисциплины (17 часов лекций, 33 часа самостоятельных занятий, курсовая работа) в неё не вошли такие разделы как реле, электромагнитные пневмо и гидрораспределители и датчики. Эти разделы изучаются студентами в курсе «Электропневмоавтоматика».

В основу пособия положены курсы лекций, которые автор на протяжении многих лет читал в МГИУ. При его написании были использованы результаты собственных научных исследований, а также публикации других авторов.

3

ВВЕДЕНИЕ

«Коммунизм – это есть Советская власть плюс электрификация всей страны». В.И. Ленин.

И хотя от коммунизма и Советской власти мы уже отказались, всё же заключительная часть этой формулы актуальна не только до настоящего времени, но и на обозримое будущее. По крайней мере, в отношении электрификации Ленин был прав. Дело в том, что электроэнергия легко преобразуется практически в любые другие виды энергии, в том числе и в механическую. Причём известны способы преобразования электрической энергии в другие виды, а также преобразования разных видов энергии в электрическую. Кроме того, успешное применение электрических сигналов в измерительных, вычислительных, информационных и других целях делает электрический вид энергии узловым. На обозримую перспективу у электрической энергии альтернативы нет в отличие от коммунизма.

Механическая энергия интересует человечество, как никакая другая : необходима замена тяжёлого ручного труда; необходима замена монотонных, однообразных механических операций; необходимы механические манипуляторы, выполняющие работу со скоростью и точностью, не доступной человеку. Говорят, что самые гениальные изобретатели – люди ленивые. Им лень работать самим. Они изобретают машины, которые выполняют их работу.

Электромеханика изучает взаимодействие электрических и механических систем в статических и динамических режимах.

Преобразователи электрической энергии в механическую можно разделить на две группы:

►силовые исполнительные устройства (электропривод: электродвигатели постоянного и переменного тока, а также силовые электромагниты);

►исполнительные устройства средств автоматики (электромагнитные коммутаторы, распределители, манипуляторы и т.п.).

Преобразователи механической энергии в электрическую также можно разделить на две группы:

►силовые генераторы и преобразователи электроэнергии;

►датчики (измерительные и сигнальные преобразователи). Силовые преобразователи отличаются от аппаратов автоматики в

большинстве случаев лишь назначением, притом, что они могут иметь один и тот же принцип действия и подобную конструкцию. Назначение силовых устройств определяет взаимосвязь: чем больше мощность – тем лучше. Например, чем больше мощность силового генератора – тем большее количество потребителей к нему можно подключить. В то же время, для датчиков, измерителей и других средств автоматики в большинстве

4

случаев справедлива обратная взаимосвязь: чем меньше мощность – тем лучше. Например, если генератор используется для измерительных целей (тахогенератор), то большая мощность вредна, поскольку это увеличивает нагрузку на исследуемую механическую систему.

1. МАГНИТНЫЕ ВЕЛИЧИНЫ И МАТЕРИАЛЫ

1.1. Магнитные величины

Причиной возникновения магнитного поля является электрический ток. Это либо гальванический ток, либо микротоки намагниченности, вызванные доменной структурой ферромагнетиков. Взаимосвязь между галь-

ваническим током I и индукцией B магнитного поля в произвольной точке A, находящейся в вакууме, (рис. 1.1) определяется законом Био-Савара- Лапласа:

где: dl – элемент проводника, создающий индукцию магнитного поля и

совпадающий с направлением тока; r – радиус-вектор, направленный из центра проводника в точку A (см. рис. 1.1); μ0 – магнитная постоянная.

Индукция B – величина векторная и дифференциальная (характери-

зует поле в точке). Направление вектора B определяется из векторного

произведения в выражении (1.1), в соответствии с которым вектор B пер-

пендикулярен к плоскости, в которой лежат векторы dl и r , и направлен таким образом, чтобы из его конца было видно кратчайшее вращение век-

тора dl в сторону вектора r против часовой стрелки.

Модуль индукции можно получить, раскрыв выражение (1.1):

B = 4μπ0 rI2 dl Sin(α) ,

где: α – угол между векторами dl и r .

Упростить применение закона Био-Савара-Лапласа можно с помощью мнемонического правила буравчика (правоходового винта или штопора – кто, чем пользуется). Буравчик (рис. 1.2) нужно вращать так, чтобы его поступательное движение совпадало с направлением тока, тогда вращение буравчика будет совпадать с направлением магнитной индукции.

На рис. 1.1 показан график зависимости модуля индукции В от расстояния r. В середине проводника индукция равна нулю в силу симметричного расположения всех силовых линий тока I. По мере смещения точки A и роста несимметрии индукция растёт и достигает максимума на по-

5

верхности проводника. При удалении от проводника индукция уменьшается по закону обратного квадрата (см. выражение 1.1). При этом вблизи проводника у зависимости наибольший градиент, а в нуль индукция обращается лишь в бесконечности.

В системе единиц СИ магнитная индукция измеряется в теслах (Тл). Если магнитное поле с индукцией B(x, y) проходит сквозь площадку

S, то все силовые линии поля в сумме образуют магнитный поток Ф.

Ф = ∫B ds Cos(B, n) = ∫Bn ds ,

S S

где: n – единичный вектор, нормальный к площадке S, а Bn – нормальная составляющая вектора индукции.

I

r

В системе единиц СИ магнитный поток измеряется в веберах (Вб). На рис. 1.3 показаны силовые линии (линии индукции) магнитного

поля, образованного длинной обмоткой с током. Из этой картины поля видно, что сквозь виток, расположенный посредине обмотки, проходят все силовые линии поля, т.е. магнитный поток самый большой. А сквозь витки, расположенные на торцах, некоторые силовые линии не проходят, т.е. с ними связан меньший магнитный поток. Сумма потоков, пронизывающих отдельные витки обмотки, называется потокосцеплением

Ψ = Ф1 + Ф2 + Ф3 + ... + ФW ,

где: w – число витков в обмотке.

6

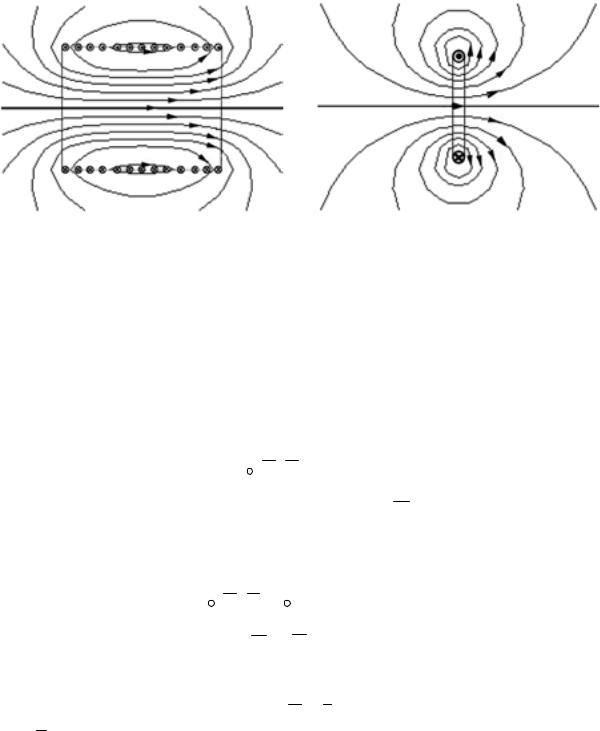
Если все витки обмотки пронизываются одинаковым потоком, как, например, у короткой обмотки (рис. 1.4), то

Ψ = w Ф. (1.3)

В системе единиц СИ потокосцепление, как и магнитный поток, измеряется в веберах (Вб).

Впоследнем выражении коэффициент L называется индуктивностью.

Всистеме единиц СИ индуктивность измеряется в генри (Гн).

Ещё одной величиной, характеризующей магнитное поле, является напряжённость магнитного поля H. Существо этого понятия вытекает из

закона полного тока:

∫(H dl) = ∑I .

l

В этом выражении слева – циркуляция вектора H вдоль замкнутого контура l. Справа – алгебраическая сумма токов, протекающих сквозь замкнутый контур l. Скалярное произведение под знаком интеграла можно раскрыть следующим образом:

∫(H dl) = ∫H dl Cos(α) ,

l l

где: α – угол между векторами H и dl .

В качестве примечания следует отметить, что закон полного тока в дифференциальной форме обращается в первое уравнение Максвелла:

rot(H ) =δ ,

где: δ – плотность тока в данной точке.

Представим себе тор, образованный обмоткой с числом витков w (рис. 1.5), внутри которого вакуум. Тогда закон полного тока будет выглядеть так:

7

где: lСР – длина средней линии тора.

Рис. 1.5

С учётом симметрии можно утверждать, что в любой точке средней линии напряжённость поля одинакова (H = Const), и закон полного тока превращается в ещё более простое выражение:

H lCP = Iw. (1.6)

Величина Iw называется магнитодвижущей силой (МДС). Подобно тому, как ЭДС в электрической цепи вызывает ток, МДС вызывает магнитный поток в магнитной цепи. Направление МДС и потока совпадают и определяются по правилу буравчика. В системе единиц СИ магнитодвижущая сила измеряется в амперах (ампервитках).

Из выражения (1.6) видно, что величина H – дифференциальная (удельная) характеристика. В системе единиц СИ напряжённость магнитного поля измеряется в амперах, делённых на метр (A/м).

Таким образом, имеется две дифференциальные характеристики магнитного поля в точке: индукция магнитного поля B и напряжённость магнитного поля H. Их соотношение для вакуума

HB = μO = 4π 10−7 Гнм .

Величина μO называется магнитной постоянной или абсолютной магнитной проницаемостью вакуума.

1.2. Магнитные материалы

Если же магнитное поле распределено не в вакууме, а в какой-либо среде, то при том же токе в обмотке (при той же МДС или напряжённости H) магнитная индукция B (магнитный поток Ф) может быть больше

8

быть больше или меньше, чем в вакууме, в зависимости от свойств среды. Для того чтобы учесть влияние среды на магнитное поле, вводится дополнительный коэффициент. Поэтому для среды имеем:

где: μ – относительная магнитная проницаемость среды – безразмерный коэффициент, зависящий от свойств среды и показывающий, во сколько раз индукция магнитного поля в данной среде больше, чем в вакууме при том же токе в обмотке. Если в среде магнитное поле усиливается, то μ > 1. Если ослабляется, то μ < 1. Для вакуума μ = 1.

В зависимости от значения μ все вещества делят на пять групп.

► Диамагнетики ослабляют внешнее магнитное поле (μ < 1) из-за того, что их атомы и ионы приобретают магнитный момент, направленный встречно внешнему полю. Диамагнетизм присущ всем без исключения веществам, но проявляется слабо и часто подавляется другими эффектами. Например, у самого сильного диамагнетика, монокристалла графита,

μ = 0,99943, у висмута μ = 0,999824, у воды μ = 0,999991. Диамагнетики проявляют себя тем, что выталкиваются из неоднородного магнитного поля. В однородном поле диамагнитные тела стремятся расположиться поперёк поля. Диамагнетики применяют в магнитных опорах без трения.

► Парамагнетики усиливают внешнее магнитное поле (μ > 1), поскольку их атомы и ионы имеют собственный магнитный момент, ориентированный согласно с внешним полем. Проницаемость парамагнетиков также очень мало отличается от единицы. У платины μ = 1,00036, у воздуха μ = 1,00000038. Кроме того, к парамагнетикам относятся вольфрам, алюминий, азот и другие вещества и соединения. Парамагнетик, помещённый в неоднородное магнитное поле, втягивается в область с максимальной индукцией, а в однородном поле стремится расположиться вдоль силовых линий поля. Некоторые парамагнитные химические соединения, например, квасцы Fe2(NH4)2(SO4)4 24H2O, применяют для адиабатического размагничивания при получении сверхнизких температур (ниже 0,3К).

► Ферромагнетики значительно усиливают магнитное поле (μ >> 1). Относительная магнитная проницаемость ферромагнетиков может быть от нескольких единиц до 106. К таким материалам относятся железо, никель, кобальт и их соединения и сплавы. Сила, которая втягивает ферромагнетик в точку поля с максимальной индукцией, во много раз больше, чем для парамагнетика.

Ферромагнетики обладают атомным магнитным порядком, при котором даже в отсутствие внешнего поля магнитные моменты атомов и ионов находятся в состоянии самопроизвольного упорядочения. При этом между атомами существуют обменные силы, противодействующие тепловому движению электронов. Под действием этих сил магнитные моменты групп

9

атомов ориентируются параллельно и образуют микрообъемы – домены, с самостоятельной (спонтанной) намагниченностью.

► Антиферромагнетики обладают атомным магнитным порядком, при котором даже в отсутствие внешнего поля энергетически выгодно образование доменов с антипараллельным расположением соседних атомных моментов. При этом результирующие магнитные моменты каждого домена равны нулю.

К антиферромагнетикам относятся хром, марганец и некоторые окислы, например, окись марганца MnO. Относительная магнитная проницаемость у них немного больше единицы и сильно зависит от температуры. При нормальной температуре μ для большинства антиферромагнетиков имеет значения одного порядка с парамагнетиками.

► Ферримагнетики также обладают атомным магнитным порядком, при котором даже в отсутствие внешнего поля энергетически выгодно антипараллельное расположение соседних атомных моментов. Но у этих материалов отсутствует взаимная компенсация магнитных моментов атомов

ирезультирующий магнитный момент доменов не равен нулю.

Кферримагнетикам в основном относятся ферриты – соединения окиси железа Fe2O3 с окислами других металлов. Например, никелевый

феррит NiO Fe2O3. Большинство магнитных свойств ферритов аналогичны свойствам ферромагнетиков, хотя магнитная проницаемость у них несколько ниже.

Материалы из трёх групп: диамагнетики, парамагнетики и антиферромагнетики имеют магнитные свойства, мало отличные от свойств вакуума. Поэтому они не нашли широкого применения в электромеханических системах и применяются лишь в специальных устройствах. Эти три группы мы оставляем без подробного рассмотрения. Нас интересуют ферромагнетики и ферримагнетики. Поскольку магнитные характеристики этих двух материалов схожи, рассмотрим их на примере ферромагнитных материалов.

1.3. Свойства ферромагнитных материалов

Все ферромагнетики характеризуются:

►большим значением относительной магнитной проницаемости, а также нелинейной её зависимостью от напряжённости поля и температуры;

►гистерезисом (вебер-амперная характеристика имеет вид петли);

►точкой Кюри, т.е. температурой, выше которой материал теряет ферромагнитные свойства и становится парамагнетиком (при охлаждении ферромагнитные свойства возвращаются).

Основная характеристика ферромагнитных материалов – зависимость индукции B от напряжённости H магнитного поля. Для получения искомой зависимости B = f(H) возьмём тор, образованный обмоткой с чис-

1 0