Исследуемые материалы

Исследования пластичности проводились нажаропрочных легированных силуминов АЛ25 (АК12М2МгН, ГОСТ 2685-75) и КС-740 (ТУ 48-26-35-75), применяемых для поршней двигателей внутреннего сгорания.

Таблица 3. Химический состав поршневых алюминиевых сплавов (%).

Сплав	Si	Mg	Mn	Cu	Ti	Ni
АЛ25	11-13	0,8-1,3	0,3-1,3	1,5-3,0	0,05-0,2	0,8-1,3
КС-740	16,5-19	0,7-1,2	-	1,8-2,4	-	1,1-1,7

Проведение экспериментов и обработка результатов

Таблица 4. Факторы, влияющие на пластичность

Факторы	Уровни
Содержание кремния в сплаве, %	12	18
Температура, оС	420	480
	-0,2	0			0,4
Скорость деформации, с-1:
При растяжении	0,01		0,1	25
Присжатии	0,01		0,074	25
При кручении	0,0154		0,18	2,825

Проведен полный факторный эксперимент. Выполнена рандомизация опытов с помощью случайных чисел. На каждом уровне не менее трех образцов. Кроме того, проведена серия дополнительных испытаний на кручение при различных скоростях деформации в диапазоне скоростей от 0,0154 до 2,825 с-1.

Для поддержания приблизительно постоянной скорости деформирования при работе на испытательной машине скорость движения траверсы корректировали по мере растяжения или осадки образца.

Показатель напряженного состояния K при растяжении вычисляли по формуле Бриджмена-Колмогорова:

K=,

где R – радиус образующей образца в месте разрушения.

Поскольку при растяжении радиус R непрерывно изменяется от ∞ до ~10 мм, величина k постепенно возрастает от 0,33 до ~0,5. В среднем было принято k=0,4.

Показатель напряженного состояния при осадке в точке наиболее вероятного разрушения определялся путем поэтапного измерения деформации в окрестностях точки. Для этого на поверхности образца была нанесена координатная ячейка размером 1х1 мм. Поскольку оси образца совпадали с главными осями тензоров, а нормальное радиальное напряжение на поверхности образца равно нулю,

,

где – радиальная скорость деформации;

;

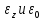–осевая и тангенциальная скорости деформации, определенные по изменению размеров координатной ячейки.

Таблица 5. Изменение k в зависимости от деформации образца

φ	0	0,21	0,36	0,57	0,90	1,14	1,29	1,53	1,72	2,06
k	-0,333	-0,285	-0,261	-0,249	-0,220	-0,183	-0,152	-0,147	-0,157	-0,162

В среднем было принято считать k=-0,2, что согласовалось с данными Г.А. Смирнова-Аляева.

Предельную деформацию λр при растяжении определяли по измерению площади поперечного сечения образца в месте разрушения

,

гдеи– начальный и конечный диаметры образца; предельную деформацию при сжатии – по формуле

,

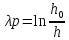где- начальная высота образца,– высота образца в момент появления первой трещины.

Для установления предельной деформации при кручении на образец до испытания наносили продольную метку, которая при скручивании превращалась в винтовую линию. Предельную деформацию находили как

,

где– угол наклона метки к образующей образца.

Результаты испытаний в виде зависимости предельной деформации от скорости позволяют определить величины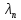, a, b. Определивнепосредственно из графика, подбираем коэффициенты a и b таким образом, чтобы в конце испытания величина Ψ принимала значение Ψ =1. Построив зависимостиот k найдем значения k_x, k_n и A.

Таблица 6. Результаты расчетов

Сплав	Температура, 0С	a	b	A	kx	kn
АЛ25	420	2	0,024	9,1	0,85	-1,8
	480	2	0,0225	10	1,0	-1,74
КС-740	420	2	0,043	15,2	0,65	-3,23
	480	2	0,041	10,3	0,65	-2,27

Обозначения на графике (рисунок 31): ∆ – растяжение

о – кручение

х – сжатие

↑ –образец не разрушился

а)

б)

Рисунок 31. Пластичность сплава АЛ25 при 420⁰С (а) и 480⁰С (б)

а)

б)

Рисунок 32 Пластичность сплава КС-740 при 420⁰С (а) и 480⁰С(б)

∆ – растяжение

о – кручение

х – сжатие

↑ – образец не разрушился

Рисунок 33. Зависимость от k, где

1 – 480 ^оС

2 – 420 ^оС

– АЛ25

- - - - КС-740

Проверка адекватности выбранной математической модели оценки пластичности проведена по критерию Фишера:

,

где– дисперсия относительного среднего;

;

где N – общее число экспериментов; среднеез начение предельной деформации;

;

–остаточная дисперсия; ;

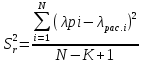K – число факторов; расчетное значение предельной деформации.

В результате обработки данных экспериментов были получены следующие величины:

= 1,464; ;; N = 166; k = 4;= 15,3.

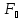должна быть больше критического значениядля степеней свободы:

= 165 и .

Для уровня значимости α = 0,05; 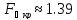, что меньше. Следовательно, модель выбрана правильно.

Поскольку фактическое значение Ψр в момент разрушения может быть ниже расчетного, необходимо определить интервал, в который попадали бы с заданной вероятностью значения Ψ<1, ограничив допустимые при деформации поковок величины Ψ нижней границей Ψр1 этого интервала. Для нахождения указанного интервала построена гистограмма значений Ψ<1 (рисунок 34).

Рисунок 34. Гистограмма значений Ψ<1

Будем считать, что гистограмма симметрична из-за отсутствия смысла расчета предельной деформации большей, чем предельная деформация, соответствующая Ψ=1.

Объем выборки n = 2m, m = 62 – число значений Ψр<1. Число интервалов k, на которые разбивается диапазон наблюдений, должно быть не менее k = 1 + 3,2lgn≈ 8. Принято k = 10. Допустили, что распределение нормальное, тогда математическое ожидание

.

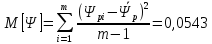Среднеквадратическое отклонение. Оценка близости эмпирического и теоретического распределения проводилась с помощью критерия Пирсона:

,

где p_i – теоретическое значение плотности вероятности в интервале с индексом i. Число степеней свободы f распределения x² равно, где l = 3– число связей, наложенных на частоты .

По таблице значений x² находим вероятность, которая была достаточно велика, чтобы считать гипотезу о нормальном распределении верной.

Вычисляем функцию Лапласа:

.

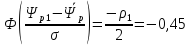По таблице значений функций Лапласа находим

.

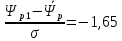Отсюда было найдено

.

Таким образом, предельная величина, при которой возможноа деформация без разрушения, должна была быть ограничена значениями.

Приэтом вероятность брака по трещинам будет составлять примерно 5%.