2 Уравнение Самуэльсона
Уравнение Самуэльсона моделирует связь между изменением цены р и неудовлетворенным спросом D(p) — S(p), где D(p) — функция спроса, S(p) — функция предложения при цене р.
Уравнение Самуэльсона имеет вид
dp/dt = k(D(p)-S(p)), (3)
где k > 0 — коэффициент пропорциональности.
Изменение цены на товар пропорционально величине неудовлетворенного спроса на этот товар.
Предположим, что спрос и предложение задаются линейными функциями
D(p)
= a
- bp,
S(p)
=
,
(4
)
где
-
некоторые положительные числа.
С учетом (4) уравнение (3) примет вид
dp/dt
=
).
(5)
Полученное уравнение является линейным дифференциальным уравнением.
Найдем решение соответствующего ему однородного уравнения.
Имеем
,
,
,
В
качестве частного решения уравнения
(5) можно использовать стационарное
равновесное решение p(t)
=
= const,
где р*
— корень
уравнения D(p)
= S(p).
В
этом случае обе части уравнения (3) будут
равны нулю. Из уравнения (4) находим
стационарное решение:
, выраженное в виде
графика 2
29
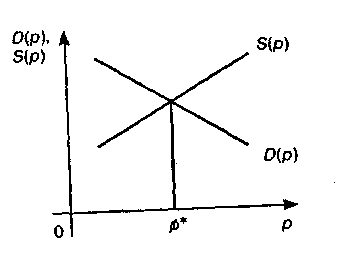
Рисунок 3 Стационарное решение Тогда общее решение уравнения (4) имеет вид
Из уравнения (5) следует, что:
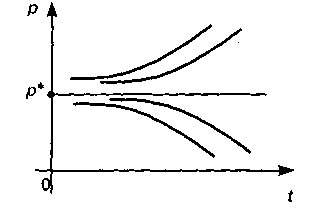
1) если
,
то
с течением времени интегральные кривые
будут отдаляться от состояния
равновесия р*
(рис.
4);
2) если
,
тоp(t)
= const
(рис. 5);
3) если
,
то
с течением времени интегральные кривые
р*
(рис.
6) будут асимптотически приближаться к
состоянию равновесия.
1
Рисунок4 Интегральные кривые, удаляющиеся от состояния равновесия
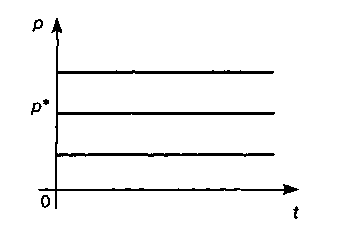
Рисунок 5 Цена постоянна во времени
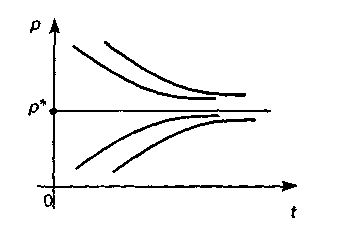
Рисунок 6 Интегральные кривые, приближающиеся к состоянию равновесия
Задание
2
- функции
спроса и предложения на некоторый товар
имеют вид
,
.
Найти
зависимость равно весной цены от времени
t,
если
в начальный момент времени цена p
= 20.
Решение. Для нахождения равновесной цены приравняем правые части
30
функции спроса и предложения: 19+р+4р'=28-2р+3р' и получим дифференциальное уравнение с разделяющими переменными:
р' = 9 - 3р, или
dp/dt =9 - 3p.
Разделим переменные: dp/(9 - 3р) = dt.
Интегрируя
обе части дифференциального уравнения
,
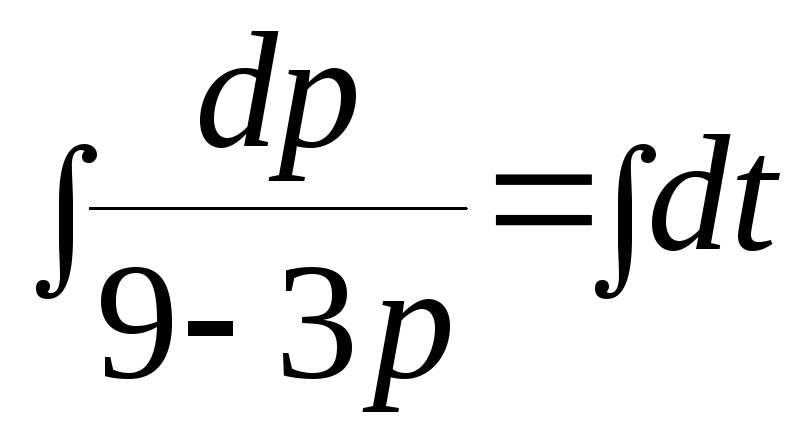получим
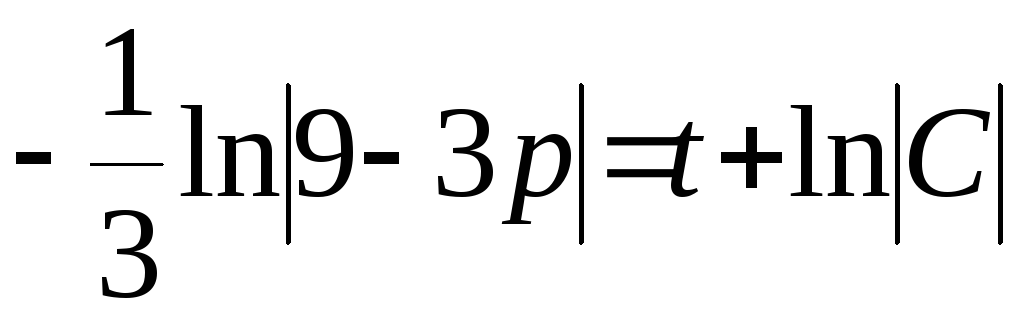или
.
Откуда
.
Подставляя
начальное условие, найдем С
и частное решение
.
Так
как
,
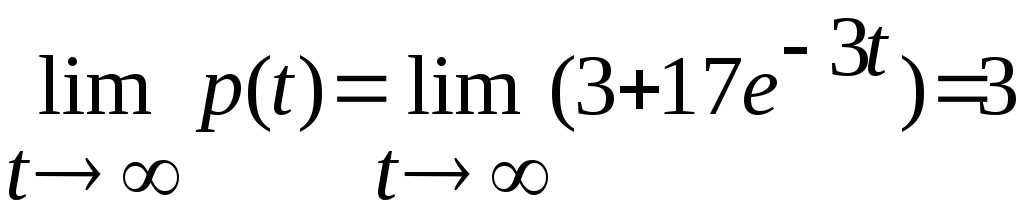то имеем устойчивое равновесие.
Заметим,
что
если
,
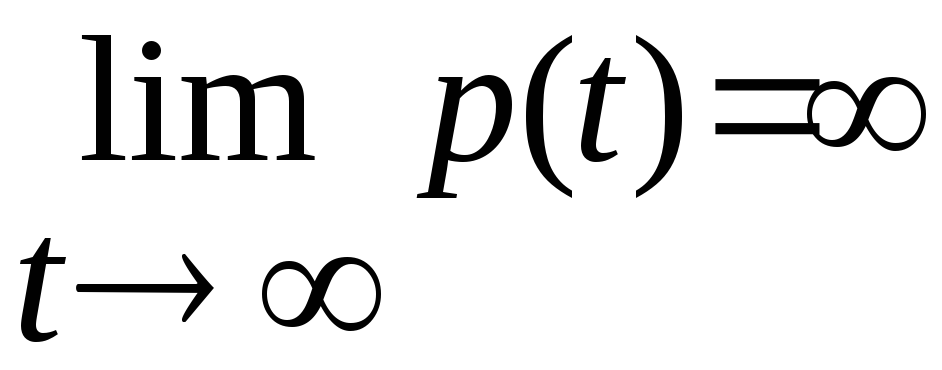то равновесная цена растет и имеет место
инфляция.
3 Модель рынка с прогнозируемыми ценами
В простых моделях рынка спрос и предложение обычно полагают зависимыми только от текущей цены на товар. Однако спрос и предложение в реальных ситуациях зависят еще и от тенденции ценообразования и темпов изменения цены. В моделях с непрерывными и дифференцируемыми по времени t функциями эти характеристики описываются соответственно первой и второй производными функции цены p(t).
Задание 3 - Пусть функции спроса D и предложения S имеют следующие зависимости от цены и ее производных:
,
S = 4p" + p' + 3p+3.
Данные зависимости вполне реалистичны, действительно:
а) спрос усиливается темпом изменения цены. Если темп растет (р" > 0), то рынок увеличивает интерес к товару, и наоборот. Быстрый рост цены отпугивает покупателя, поэтому слагаемое с первой производной функции цены входит со знаком «—»;
б) предложение в еще большей мере усиливается темпом изменения цены, поэтому коэффициент при р" в функции S больше, чем в D. Рост цены также увеличивает предложение, поэтому слагаемое, содержащее р', входит в выражение для S co знаком «+».
31
Пример. Требуется определить закон, устанавливающий зависимость цены от времени.
Пусть функции спроса D и предложения S имеют следующие зависимости от цены и ее производных:
,
S = 4p" + p' + 3p+3.
Решение. Поскольку равновесное состояние рынка характеризуется равенством D = S, получим
3р" - р' - 2р+18 = 4р" + р'+3р+3,
р" + 2р'+5р = 15. (6)
Уравнение (2.26) представляет собой неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами относительно функции p(t). Общее решение такого уравнения состоит из суммы какого-либо его частного решения и общего решения соответствующего однородного уравнения
р"+2р'+5р = 0. (7)
Характеристическое
уравнение имеет вид
.
Его корни — комплексно-сопряженные числа:
,
,
и, следовательно, общее решение
уравнения (7) имеет вид
,
где С1, С2 — произвольные постоянные.
В качестве частного решения неоднородного уравнения (2.26) возьмем решение р = р* — постоянную величину как установившуюся цену.
Подставим р = const в уравнение (2.26), получим
,
.
Тогда общее решение уравнения (2.26) имеет вид
.
Нетрудно
увидеть, что
при
,
т.е. все интегральные кривые имеют
горизонтальную асимптотур*
=
3
и колеблются около нее. Это означает,
что все цены стремятся к установившейся
цене р*
с
колебаниями около нее, причем амплитуда
этих колебаний затухает со временем.
Можно привести частное решение этой задачи в двух вариантах.
1. Задача Коши. Пусть в начальный момент времени известна цена, а также тенденция ее изменения: t = 0, р(0) = 4, р'(0) = 1.
32
Подставляя
первое условие в
,
получим
;
,
откуда
=1,
т.е. получили
.
Дифференцируя это выражение, имеем
Используем второе условие задачи Коши:
,
,
откуда С2=
1.
Окончательно получаем, что решение задачи Коши имеет вид
.
2 Смешанная задача. Пусть в начальный момент времени известны цены и спрос: t= 0, р(0) = 4, D(0) = 30. Поскольку первое начальное условие такое же, как и в предыдущем случае, то имеем решение
.
Тогда производные функции p(t) выражаются формулами
Отсюда
и
.
Подставляя эти равенства, а также р(0) = 4 и D(0) = 30 в выражение
D = 3p"-p'-2p+18, получим С2=-2.
Тогда
решение данной задачи имеет вид
Второй семестр - 8 часов
ПРАКТИЧЕСКАЯ РАБОТА № 6 - 4 часа
Тема: Планирование и анализ трудовых показателей
Цель работы: формирование практических навыков расчета трудовых показателей, характеризующих деятельность промышленного предприятия.