4 семестр / Задание №1 Численное решение уравнения переноса

Задание № 1

ЧИСЛЕННОЕ РЕШЕНИЕ ЛИНЕЙНОГО

УРАВНЕНИЯ ПЕРЕНОСА

Цель работы — изучение разностных схем и конечно-разностных методов численного решения линейного одномерного уравне­ния переноса, решение уравнения переноса по схеме бегущего счета.

ПОСТАНОВКА ЗАДАЧИ

В физических приложениях часто встречаются уравнения эволюционного типа:

где дифференциальный оператор L₀ уже не содержит производных по времени t; такие уравнения как бы описывают эволюцию начальных условий. Если L₀ — оператор первого порядка, то уравнение называется уравнением переноса и типично для задач механики сплошной среды. Примером уравнения переноса может служить известное уравнение непрерывности (закон сохранения заряда)

где  —плотность объемного заряда, — плотность тока, — скорость движения заряженной среды.

Простейшая линейная одномерная задача для уравнения переноса:

c = const (0 < x < l), u(0, t) = (t) , u(x, 0) =

описывает движение сплошной среды с плотностью u вдоль оси x со скоростью c; правая часть f описывает приток (отток) вещества вследствие каких-либо сторонних процессов. Будем также для простоты полагать, что

(0) = u⁰(0).

Для получения численного решения введем равномерную сетку с шагами h,  и узлами (x_j, t^m), где

x_j = jh (j = 0, 1, …, N),

h = l/N, t^m = m (m = 0, 1, 2, …).

Значения сеточных функций принято обозначать как

т. е. нижние индексы относятся к пространственным переменным, а верхний указывает номер момента времени. Для краткости принято в разностных схемах верхний индекс, по возможности, опускать, используя обозначения:

Расположение узлов, на котором строится разностная схема, называют шаблоном. Рассмотрим два шаблона, показанные на рис. 1; кружками отмечены узлы шаблона, а звездочкой — центр соответствующей сеточной ячейки, ограниченной штриховыми линиями.

Рис. 1. Расположение узлов разностных схем для линейного

уравнения переноса

Соответствующие двум шаблонам разностные схемы имеют вид:

(1)

(2)

Различия между двумя схемами заключается в том, что производная по пространственной координате берётся в разные моменты времени. Разностная схема (1) явная, так как из нее можно явно выразить неизвестное через уже известные значения u_j, u_j–1 и правую часть f_j. Схема (2) формально неявная, так как включает два неизвестных значения на (m + 1)-м временном слое. Однако преобразовав ее к виду

можно явно вычислить последовательно, начиная с левой границы, на которой известно (это заданное краевое условие). Такие схемы называют схемами «бегущего счета».

Рассмотрим теперь, что принять в в качестве сеточной проекции f_j правой части f. Поскольку f зависит от x, t, наименьшая погрешность аппроксимации получается при замене f(x, t) на среднее значение по площади сеточной ячейки, т. е. на значение

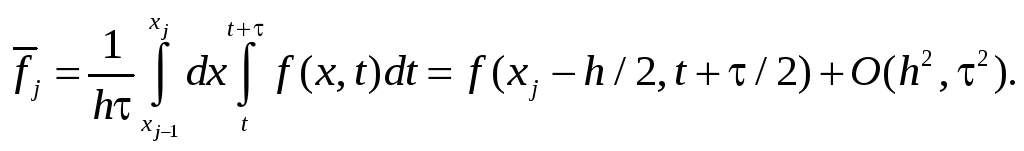
Следовательно, в уравнениях в качестве f_j будем принимать , т. е. правая часть в разностных схемах вычисляется в отмеченном звездочкой центре сеточной ячейки. Заметим, что если в качестве f_j просто принять значение в j-м узле, т. е. f(x_j, t), то погрешность аппроксимации сразу возрастает на порядок.

А

(3)

нализ устойчивости разностных схем показывает, что схема (1) устойчива при выполнении условия

0  r  1 (r = c/h),

т. е. это условно устойчивая схема. Условие устойчивости имеет простой физический смысл: вещество среды распространяется в положительном направлении оси абсцисс, причем расстояние c, на которое смещается вещество за один временной шаг , не должно превышать шаг сетки h. Информация распространяется по сетке со скоростью h/τ (сеточная скорость). Эта скорость должна быть больше физической скорости (в данном случае – скорости переноса). Сформулированный таким образом критерий (3) иногда называют критерием Куранта, а число r = c/h – числом Куранта.

Схема (2) устойчива для всех c > 0. Следовательно, данная схема безусловно устойчивая. Безусловная устойчивость — очень полезное качество разностной схемы, так как позволяет независимо подбирать временной и пространственный шаги сетки, руководствуясь лишь требуемой погрешностью решения.

Используя безусловно устойчивую разностную схему (2) найти решение уравнения переноса с заданными ниже краевыми и начальными условиями.

ВАРИАНТЫ ЗАДАНИЙ

ВАРИАНТЫ НАЧАЛЬНЫХ УСЛОВИЙ

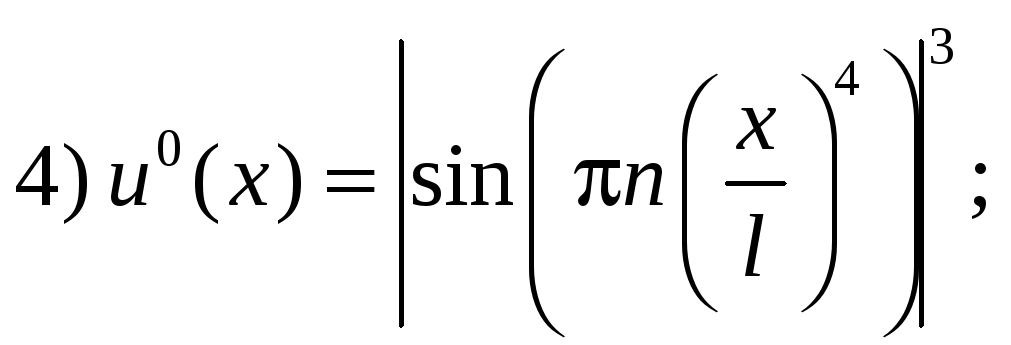
ВАРИАНТЫ КРАЕВОГО УСЛОВИЯ φ(t)

ВАРИАНТЫ ФУНКЦИЙ f(x,t)

ПРОГРАММИРОВАНИЕ

Для хранения текущих значений u_j достаточно отвести один одномерный массив размера N + 1 (N = 40 ÷100), записывая новые значения на место предыдущих. Временной шаг τ, длительность моделирования Т и число временных шагов N_t рекомендуется определить из условий

Выдачи результатов u_j (j=0, 1,...,N) следует организовать через каждые M = 10÷50 временных шагов, включая в выдачу также номер временного шага N_t и текущее время t = N_t τ. Соответственно, выдача производится, если N_t, делится нацело на М.

В заданиях функции f(x,t) и φ(t) выбраны так, что при Т>>l/с устанавливается стационарное состояние с u_j, не зависящими от t. Для проверки программы можно предваритель­но решить тестовую задачу, полагая и исследуя установление очевидного решения

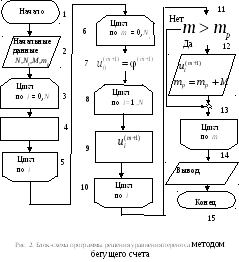
Блок-схема программы приведена на рис. 2. В цикле 3-4-5 задаются начальные, в 6-7 граничные условия, а в блоках 8-9-10 вычисляются .

СОДЕРЖАНИЕ ОТЧЕТА

Отчет должен содержать:

• формулы и параметры для конкретного варианта;

• текст программы;

• результаты решения и график распределения .

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Какова погрешность разностной схемы (2), какими свой-

ствами она обладает?

2. Нарисуйте расположение сеточных узлов («шаблонов), на

котором построена схема (2).

3. Как надо изменить схему (2) и шаблон дли расчета тече-

ний со скоростью с <0?

4. Как можно построить схему бегущего счета второго порядка?

5. Какие разностные схемы называются монотонными? Облада-

ет ли схема (2) монотонностью?

7