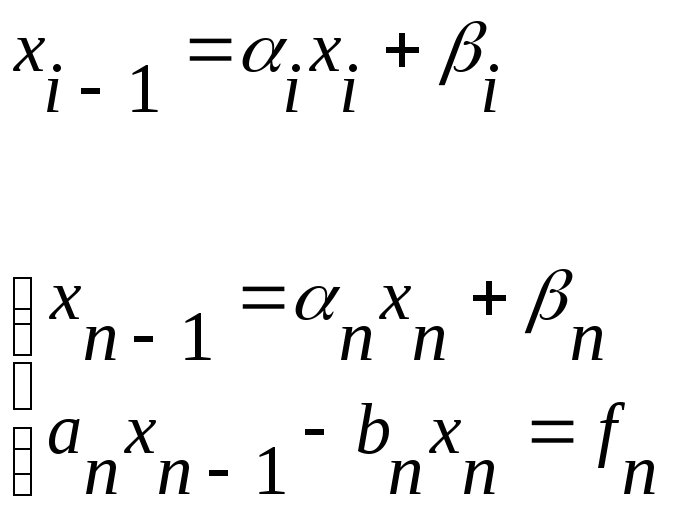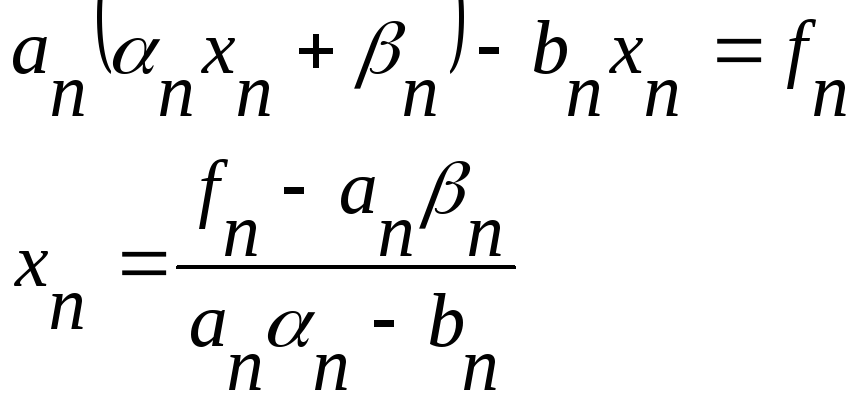gos / Obzor_Lection_VM12

Московский Инженерно-Физический Институт.

Кафедра № 17

Численные Методы.

Обзорные лекции для К10-171,172.

Лектор: Лавренюк С. Ю.

Москва 2012г.

1. Метод Гаусса.

Решаем СЛАУ:

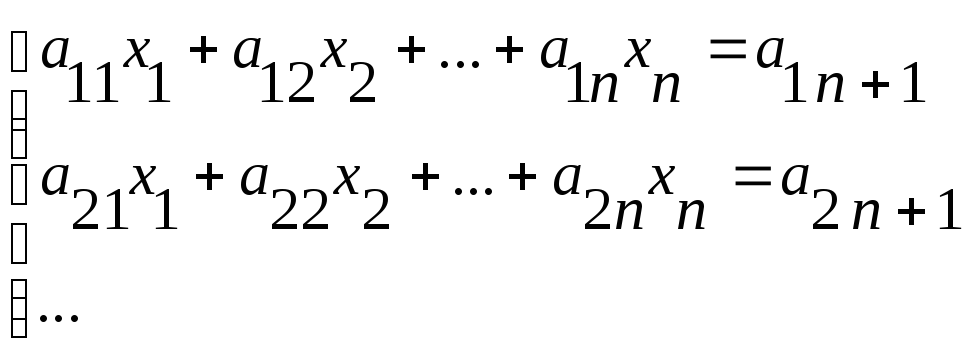
Выполняем n-1 шаг вперёд (приведение матрицы к верхнеугольной), потом n-1 шаг назад (нахождение х)

По аналогичной формуле преобразуются все нижеследующие строчки.

На (n-2)-ом шаге получается треугольная матрица.

Метод Гаусса с выделением главного элемента.

1) В текущей строке находится

2) Переставляются столбцы (то есть переименовываются х_i в х_j и наооборот), чтобы оказался спереди.

Метод дает выше точность для матриц большой размерности

2. Метод простой итерации решения СЛАУ.

Сходится, если хотя бы одна норма у B < 1 по модулю, т.е., например, если max|| < 1.

Этот метод имеет ограниченную область сходимости.

Доказательство:

Напишем это же самое в развёрнутом виде:

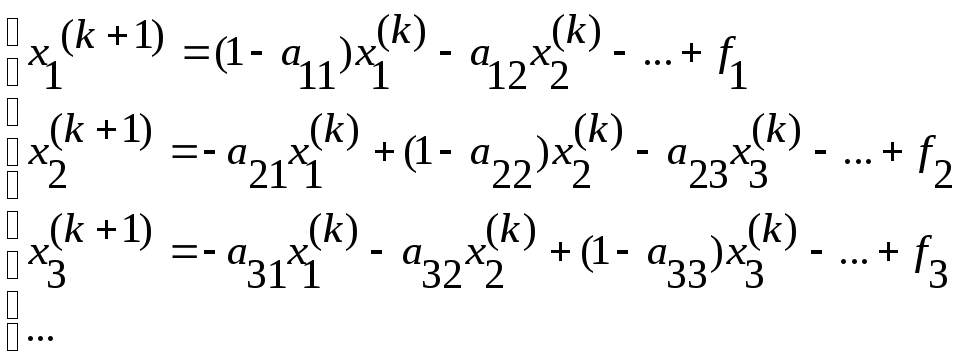
Метод Зейделя.

Усовершенствуем предыдущую систему:

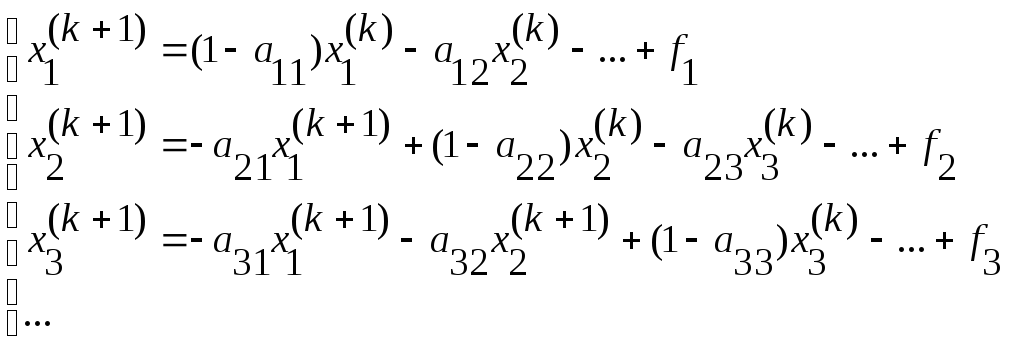
Свойства:

1. Скорость сходимости увеличивается.

2. Можно останавливаться в середине итерации (в середине цикла).

3. Области сходимости той же мощности (некоторые матрицы, которые методом последовательных приближений сходятся, методом Зейделя сходиться не будут, и наоборот).

4. Нет требования к симметричности или положительности .

Метод обеспечения сходимости метода Зейделя.

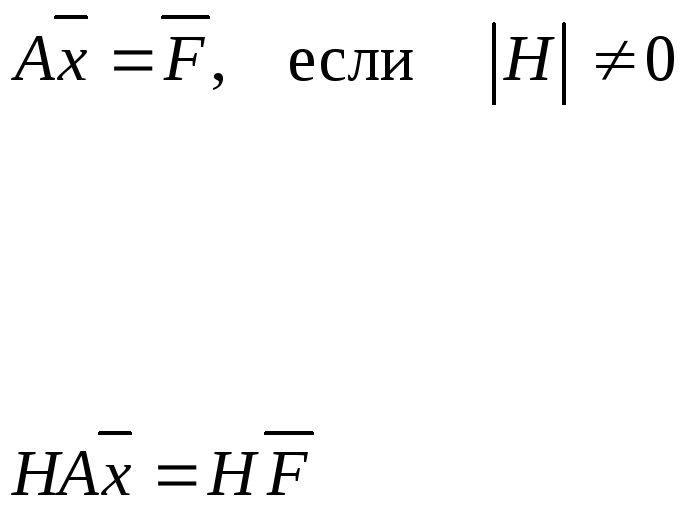
то две СЛАУ равносильны

тогда

Выбор H, чтобы все || < 1 у HA

Итерационный процесс:

1)

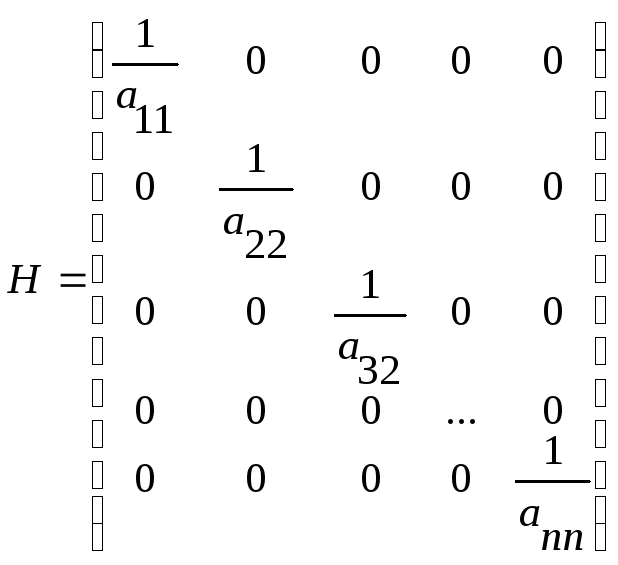
2) Если 1) не дало результата (процесс не стал сходиться).

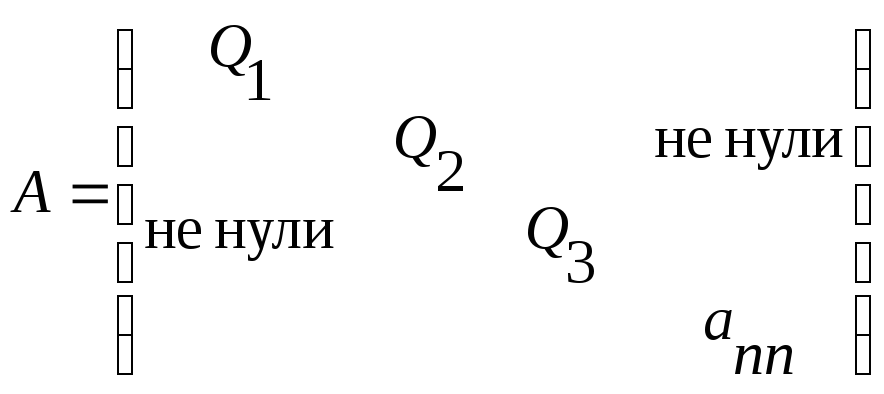
Ищем блоки 2*2, если их нечётное количество, то останется 1 блок 1*1=a_nn

3) и т. д.

3. Численное обращение матриц методом окаймления.

А:

На k-ом шаге находится обратная матрица углового минора kk, при этом известна обратная матрица для предыдущего углового минора (k-1)(k-1).

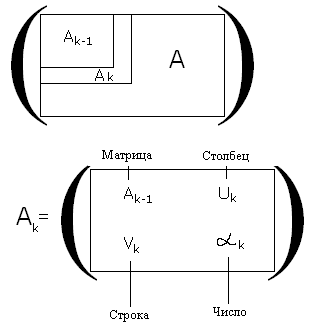
Будем искать А_k^-1 в виде (матрица):

P_k-1 r_k

q_k 1/_k

А_k*A_k^-1 = E = [A_k-1 U_k; V_k _k]*[ P_k-1 q_k; r_k 1/_k] =

[A_k-1*P_k-1+U_k*q_k A_k-1*r_k+U_k*1/_k; V_k*P_k-1+_k*q_k V_k*r_k+_k*1/_k] =

= [E_k-1 0; 0 1]

(1) A_k-1*P_k-1+U_k*q_k = E;

(2) A_k-1*r_k+U_k*1/_k = 0;

(3) V_k*P_k-1+_k*q_k = 0^T;

(4) V_k*r_k+_k*1/_k = 1;

Следовательно:

r_k = -А_k-1^-1 * U_k/_k; (5)

Где А_k-1^-1 известна на предыдущем шаге.

Подставим (5) в (4):

V_k*(-А_k-1^-1*U_k/_k) + _k/_k = 1;  _k = _k - V_k*А_k-1^-1*U_k;

Подставим в (5):

r_k = -А_k-1^-1 * U_k/_k;

Выразим из (1) P_k-1­ и подставим в (3):

q_k = -V_k*А_k^-1/_k;

P_k-1­ = А_k-1^-1 + (А_k-1*U_k*V_k А_k-1^-1)/_k.

4. Преобразование Хаусхолдера.

(Для приведения матрицы n*n к виду Хессенберга ровно за n-2 итерации)

Некоторые определения (воспоминания).

D – диагональная:

Q – ортогональная:

R – правая (верхняя) прямоугольная:

L – левая (нижняя) треугольная:

H – Хессенберга : 1) правая, верхняя

2) левая, нижняя

Подобные матрицы: если  Q, что B = Q^TAQ (у подобных матриц одинаковые собственные значения)

Конец воспоминаний

Выполняется n-2 шага (начиная с последней строки, и далее вверх).

На каждом шаге:

Исключаем нулевые элементы в очередной строке (j<i-1),

Пример i-ого шага: работаем со строкой l = n-i+1

До главн. диаг.

i =4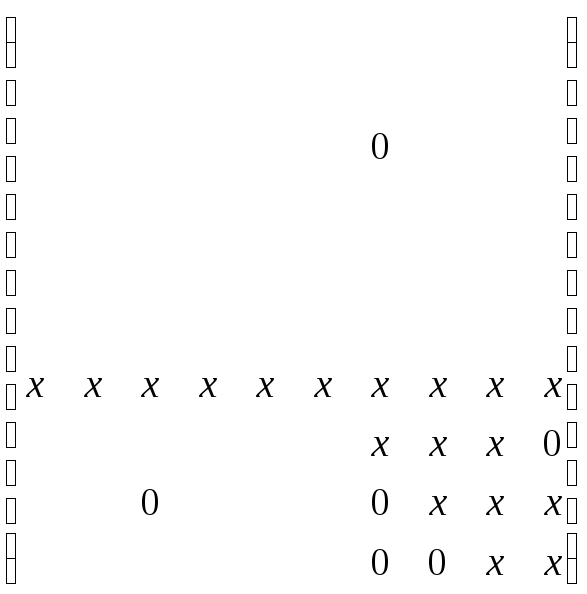

1) Рассчитывается величина

2)

3) ( это скаляр )

4) ( это матрица)

5) - (первую Р не транспонируем, т.к. матрица симметричная)

5. QR – разложение матрицы.

Задача представить матрицу А в виде произведения: , где Q – ортогональная ( -- верхнетреугольная.

Теорема: Если А – верхняя матрица Хессенберга, то у неё существует

QR – разложение, и оно осуществляется последовательным уничтожением поддиагональных нулей.

Уничтожаем а₂₁ : (в общем случае: а_ij, где j = i+1)

Берём 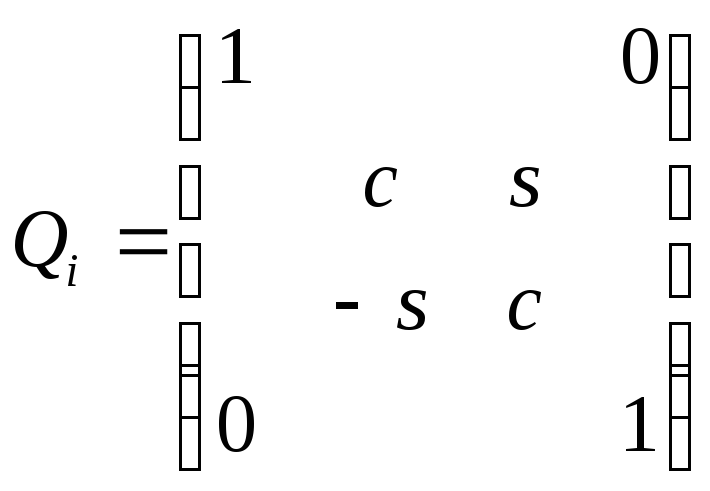, где

Получаем:

Домножим слева на

Получим:

Алгоритм:

1) Находим

2)

…

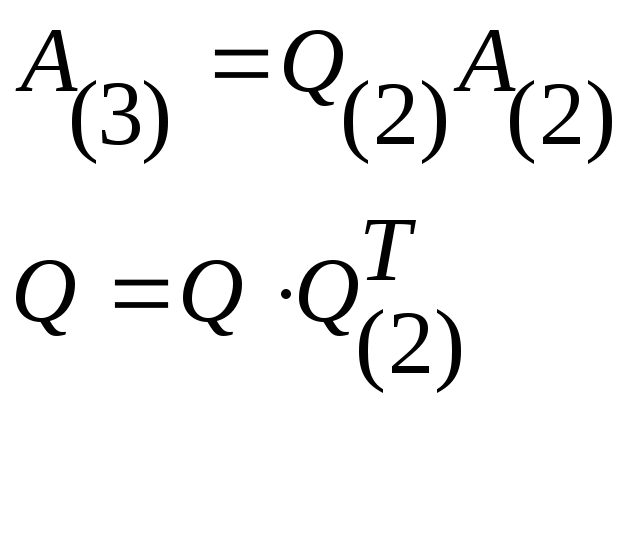
n-1)

6. Нахождение всех  у матрицы при помощи

QR – разложения.

Первоначально матрицы надо привести к виду Хессенберга. После этого можно запускать итерационный процесс.

-- раскладываем

-- перемножаем

-- раскладываем

-- перемножаем

…

Делаем, пока сумма квадратов элементов на диагонали не станет значительно больше суммы квадратов элементов под диагональю; либо пока матрица не перестаёт меняться (этот второй критерий используется, если есть комплексно-сопряжённые ).

Свойства метода.

Свойства итерационной последовательности (А_(i)).

1) В пределе получается верхне-блочнотреугольная матрица, в которой на диагонали стоят  в порядке убывания, а блоки 2*2 соответствуют комплексно-сопряжённым .

2) Если исходная была симметричная матрица (при действительных ), то получится диагональная матрица, если не симметричная, то треугольная.

Скорость сходимости определяется тем, как стремятся к нулю недиагональные элементы:

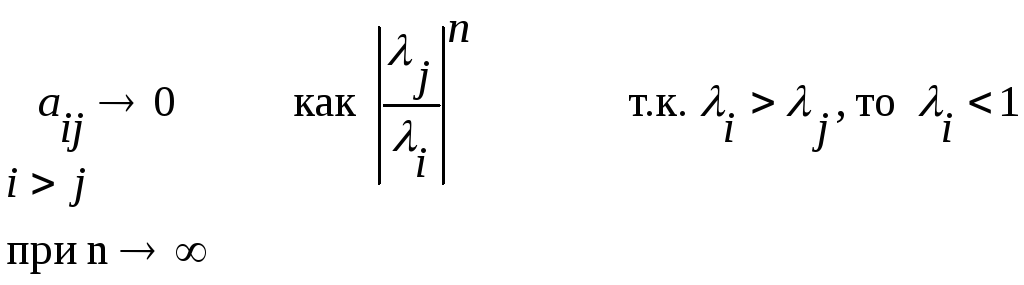
Все поддиагональные элементы на каждом шаге уменьшаются, что приводит к уменьшению суммы квадратов элементов под диагональю.

7. Нахождение всех  у матрицы при

помощи QR – разложения со сдвигом.

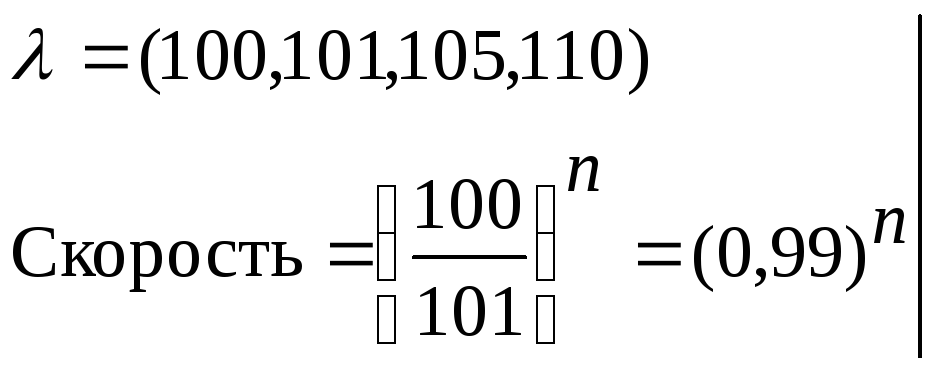Это пример, когда обычный метод QR-разложения работает медленно.

Алгоритм разложения со сдвигом:

-- раскладываем

-- перемножаем

где -- некоторые числа.

Свойства метода, свойства полученной последовательности матриц

 1) тот же (В пределе получается верхне-блочнотреугольная матрица, в которой на диагонали стоят  в порядке убывания величины -l, а блоки 2*2 соответствуют комплексно-сопряжённым .)

2) скорость сходимости: a _{i j}  0 так же, как  0

Если , то скорость -- быстрее, чем у обычного метода

Если то после (n-1) итерации все а_ij = 0.

8. Метод Рунге-Кутта 4-ого порядка.

Общая часть: Поставка задачи.

1) Задача Коши

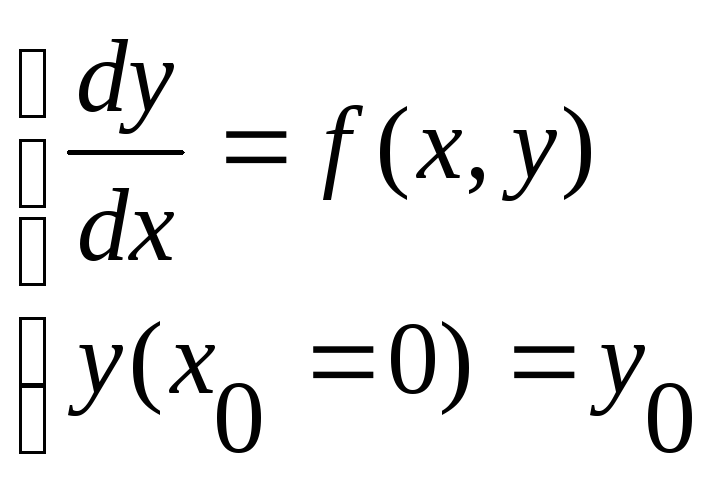
2) Система ДУ

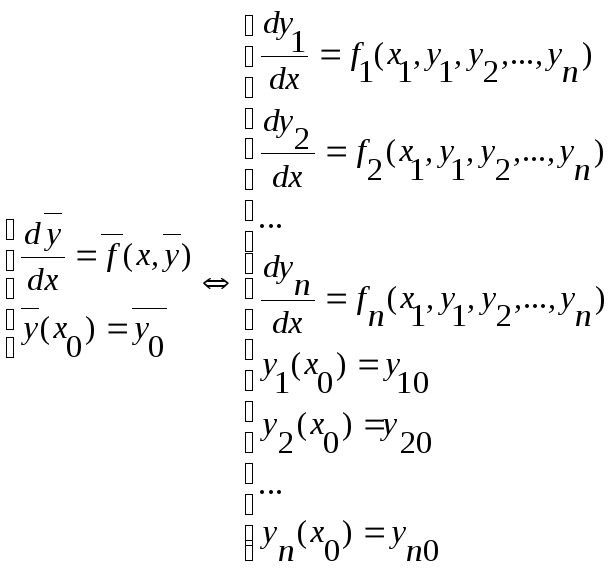
3) Уравнение с высшими производными

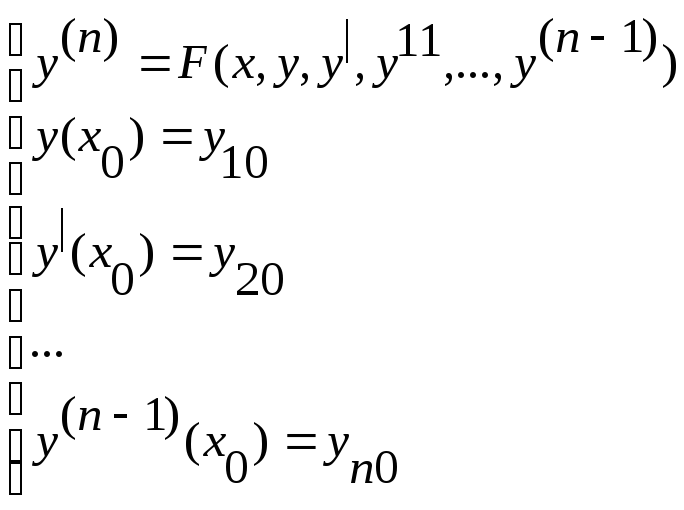тоже Задача Коши, как 1) и 2)

1), 2), 3) – одно и тоже (один вид постановки задачи может быть преобразован к другому)

Пример этого преобразования:

Для системы 5-ого порядка:

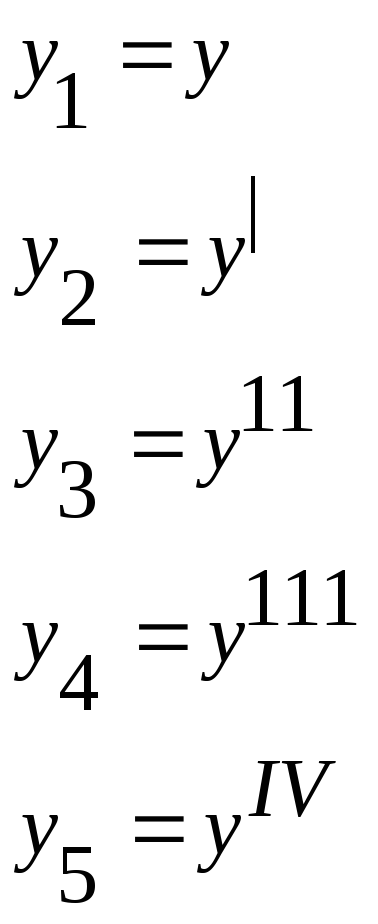
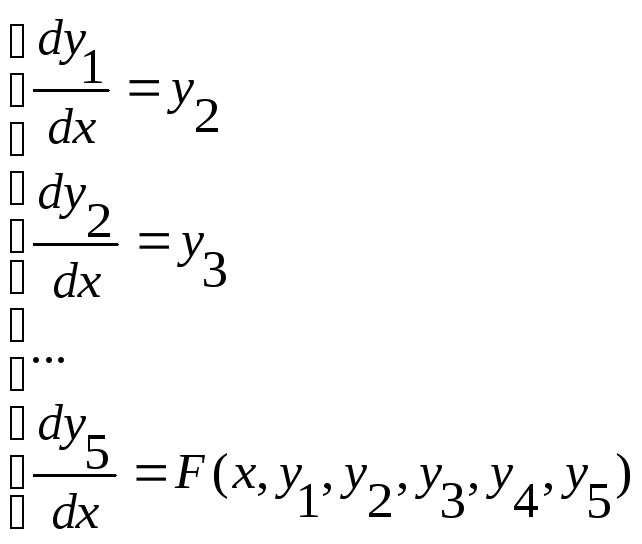
Алгоритм Рунге-Кутта:

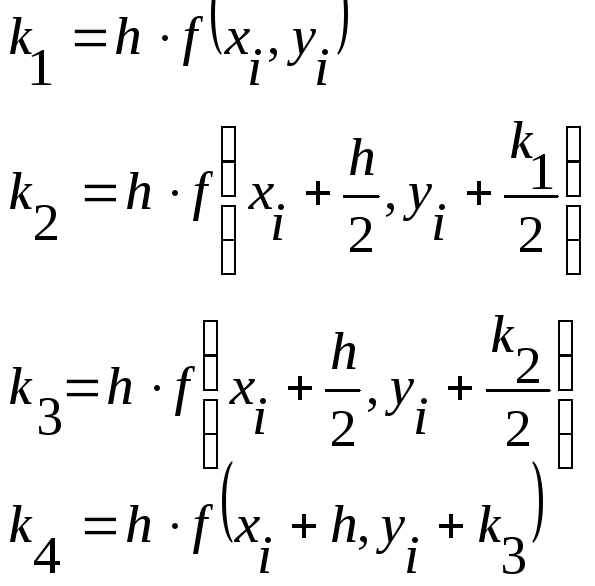
Тогда,

Для системы: всё точно также, только стоят вектора над k, f, y.

Распишем вектора в нормальном виде.

При описании k надо не забыть, что это 2-мерная матрица 4*n:

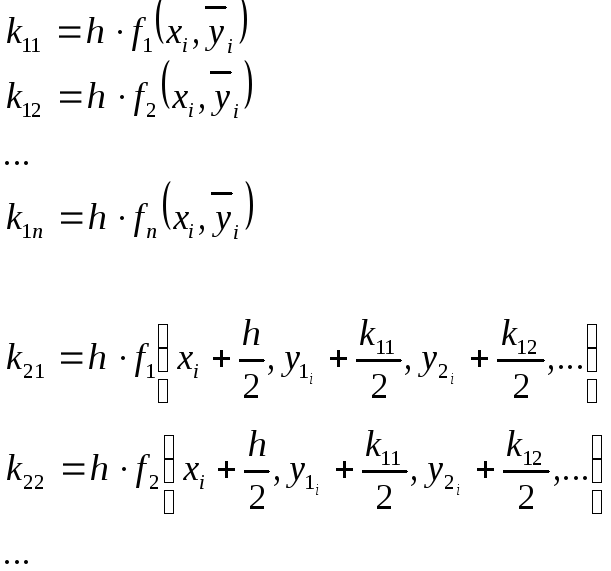
Критерий устойчивости:

Критерий точности:

(Для многомерного случая вместо берется у матрицы частных производных )

Критерий увеличения (уменьшения) шага:

(при динамическом определении шага)

если crit > порог 1, то надо уменьшить шаг, если Crit < порог 2 < порог 1, то можно шаг увеличить.

Алгоритм:

1. Считаем 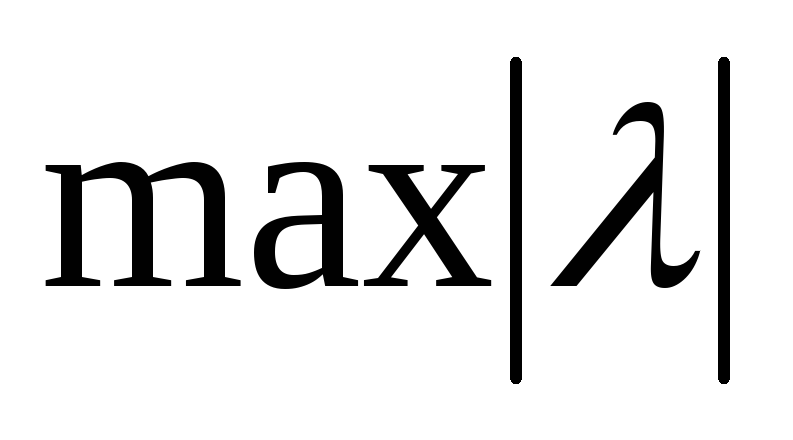у матрицы частных производных в

2. Берём

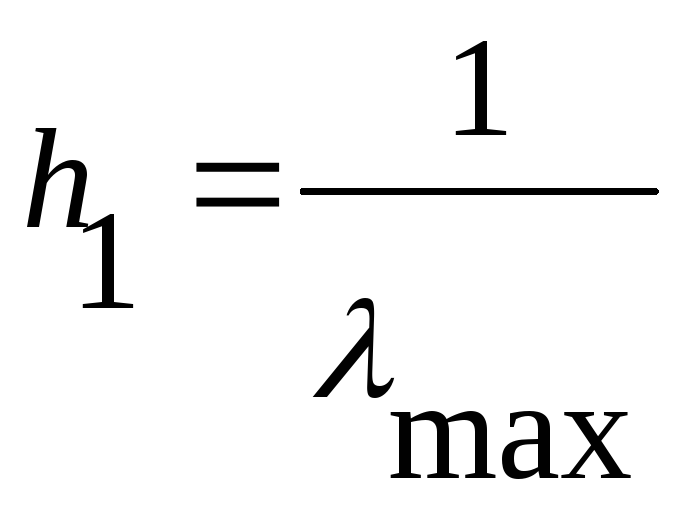
3. Делаем 1-ый шаг и считаем

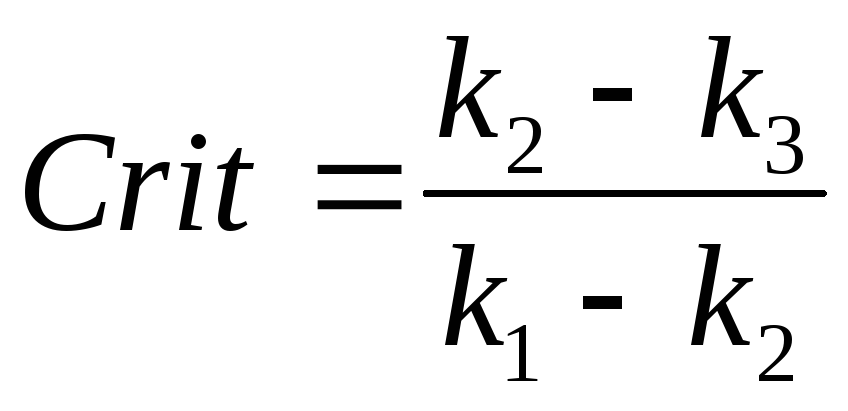
4. Устанавливаем пороги:

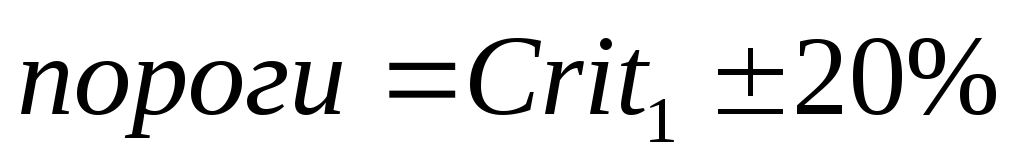
9. Метод прогноза и коррекции 4-ого порядка.

Таких методов много, отличаются значением коэффициентов коррекции.

Алгоритм:

1. Считаем 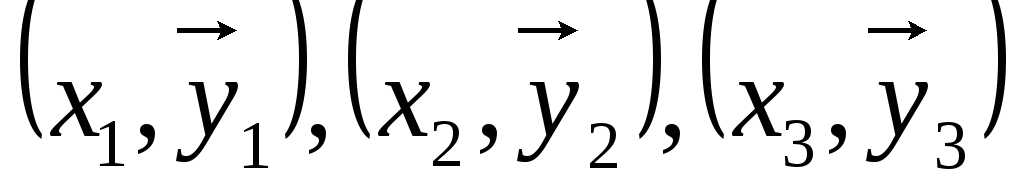методом RK4 (первые 3 шага)

Дальше собственно метод:

Делаем расчёты, исходя из прогноза, для которого нужна основа, например, 4 точки (поскольку метод 4-ого порядка) в качестве начальных условий.

2. Расчёт предсказания:

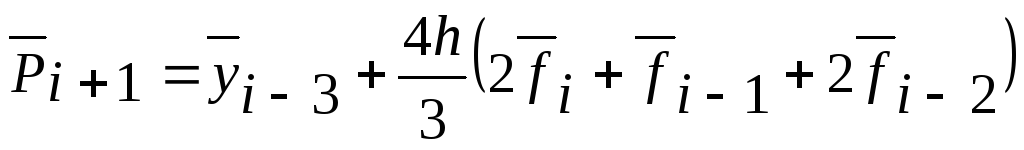
3. Изменение предсказания:

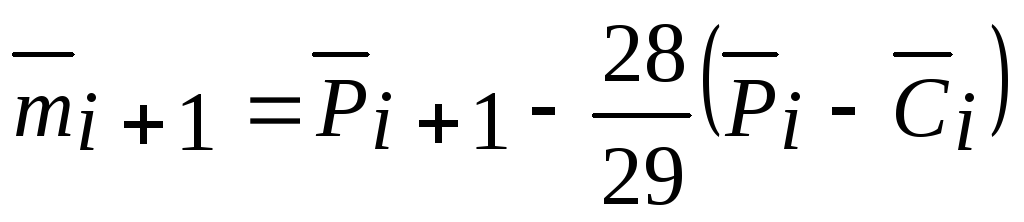
4. Изменение производной:

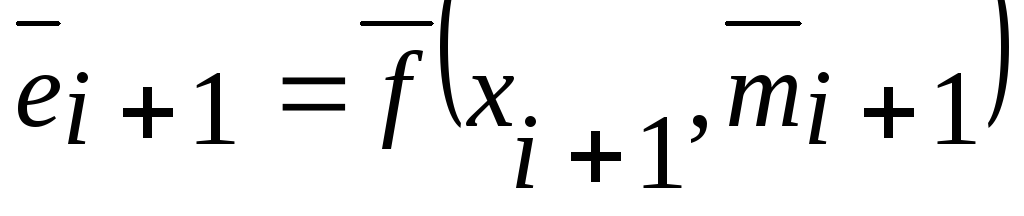
5. Коррекция:

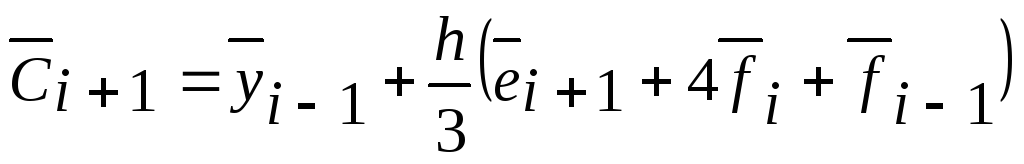
6. Значение 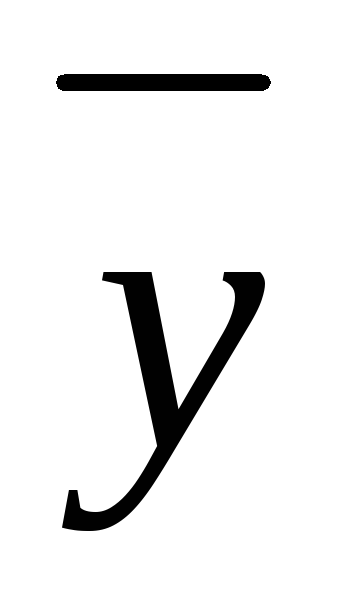в точке x_i+1:

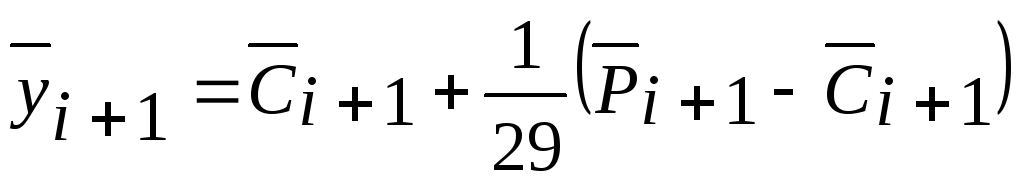
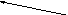
Гарантированная погрешность.

Свойства:

1. 2 раза расчёт f на каждом шаге (остальные f рассчитаны ранее)

2. Погрешность < a = o(h⁵)=

Достоинства метода: 1) маленькая погрешность

2) всего 2 раза высчитываем функцию.

Недостатки метода: не может работать самостоятельно, сначала надо прорешать несколько шагов методом RK.

10. Решение трёх-диагональных СЛАУ методом прогонки.

Решение (алгоритм):

Ищем решение в виде: , где и неизвестные пока функции.

Подставим в исходную систему:

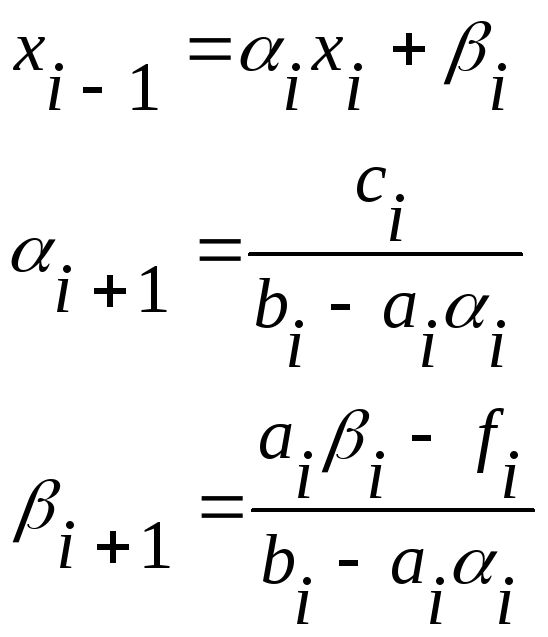
₁, ₁ берутся из 1-ого начального условия:

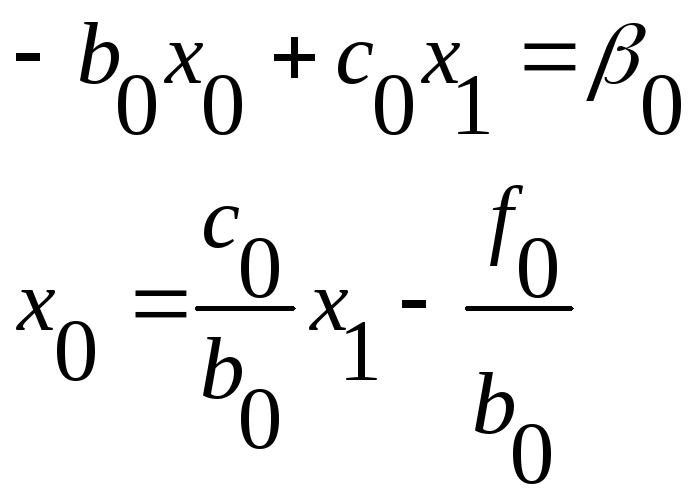
Алгоритм.

1. Находим ₁, ₁ из 1-ого начального условия.

2. Прямая прогонка: i = 1, 2, …, n-1

cчитаем все _i+1 и _i+1

3. Из последнего начального условия находим x_n

4. Обратная прогонка: i = n, n-1, …, 1

15