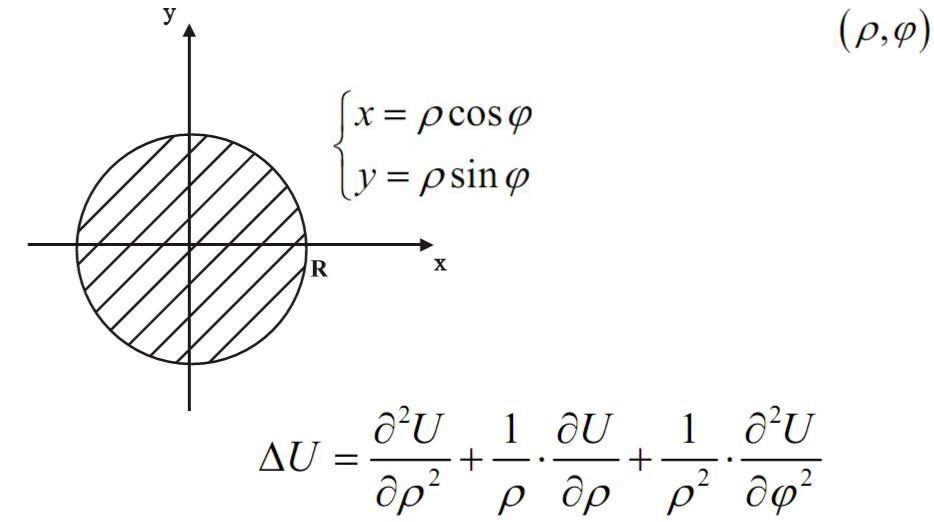
Задача Дирихле для уравнения Лапласа в круге
Введем полярную систему координат
– полярные координаты
Уравнение в полярных координатах имеет вид
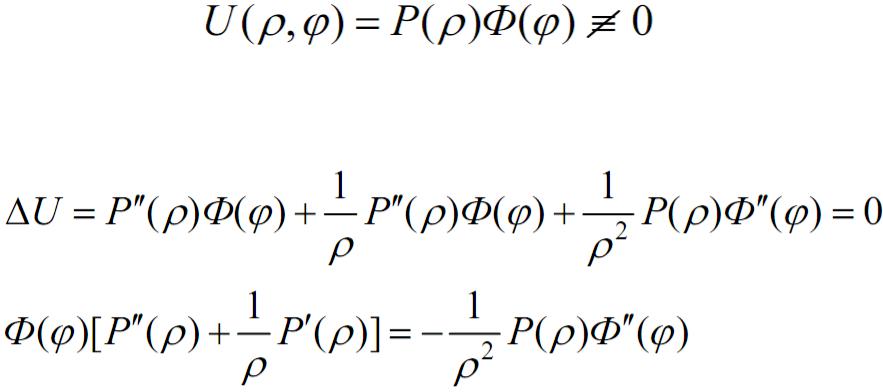
Задача Дирихле для уравнения Лапласа в круге
Решим уравнение методом разделения переменных, то есть будем искать частное решение уравнения, вида
Подставляя предполагаемую форму решения в уравнение, получим
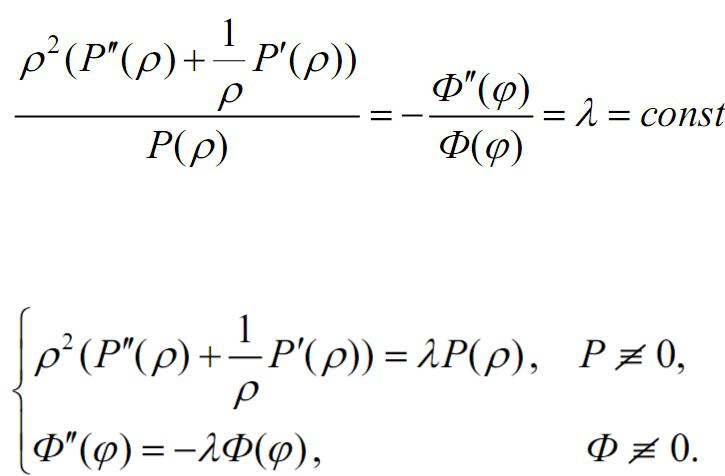
Задача Дирихле для уравнения Лапласа в круге
Отсюда получим два обыкновенных дифференциальных уравнения:
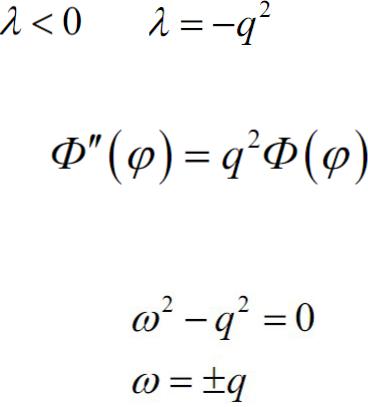
Задача Дирихле для уравнения Лапласа в круге
Определим знак λ :
1 случай
Рассмотрим уравнение
Характеристическое уравнение имеет вид
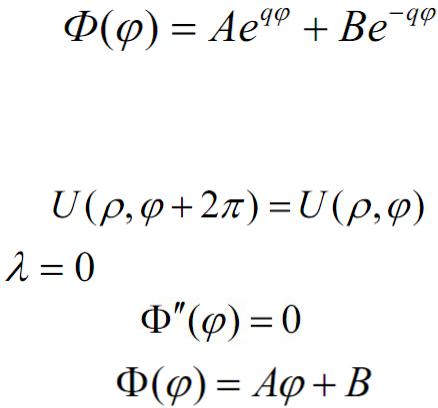
Задача Дирихле для уравнения Лапласа в круге
это решение не подходит, так как должно выполнятся условие периодичности
2 случай
-это решение подходит при условии, что A=0
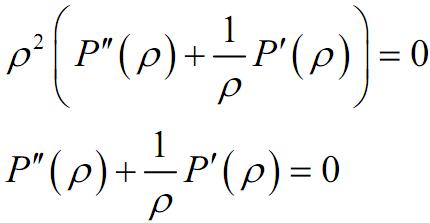
Задача Дирихле для уравнения Лапласа в круге
Рассмотрим уравнение
Пусть 
,тогда:
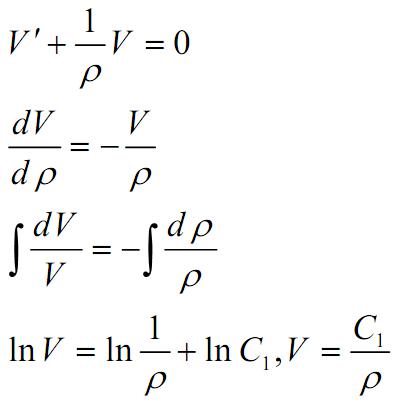
Задача Дирихле для уравнения Лапласа в круге
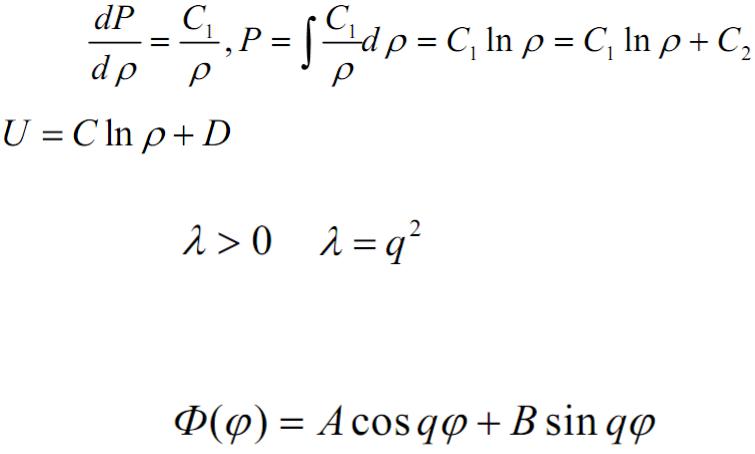
Задача Дирихле для уравнения Лапласа в круге
- решение уравнения в общем случае
3 случай
Решение уравнения
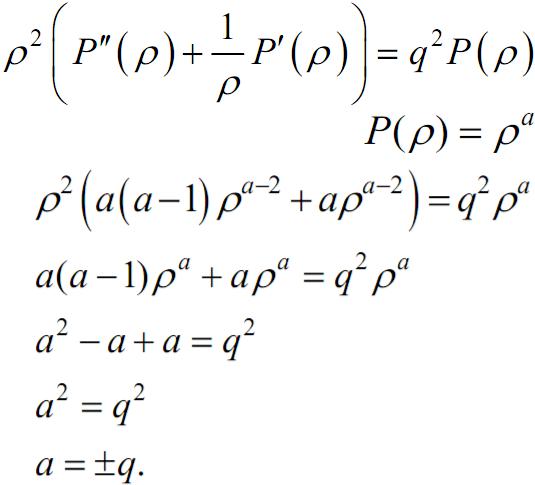
Задача Дирихле для уравнения Лапласа в круге
Рассмотрим уравнение
Решение будем искать в виде
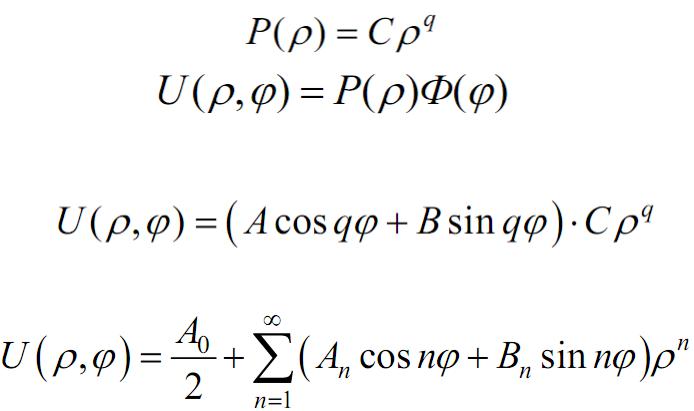
Задача Дирихле для уравнения Лапласа в круге
- решение уравнения Для решения внутренней задачи надо положить
Частные решения нашей задачи найдены:
Вид общего решение