Теорема единственности

При решении краевых задач:

1)надо убедиться в том, что дополнительные условия достаточны для выделения однозначного решения; это достигается доказательством теоремы единственности;

2)надо убедиться в том, что дополнительные условия не переопределяют задачу, т. е. Среди них нет несовместных условий; это достигается доказательством теоремы существования;

доказательство существования обычно тесно связано с методом нахождения решения.

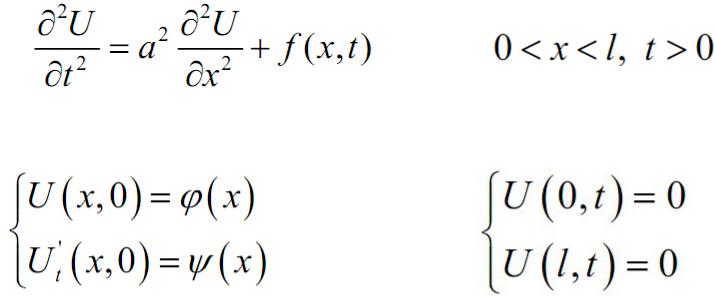
Теорема единственности для уравнения колебаний струны

Возможно существование только одной функции

U(x,t), определенной в области и удовлетворяющей уравнению

при

начальным условиям и однородным граничным условиям

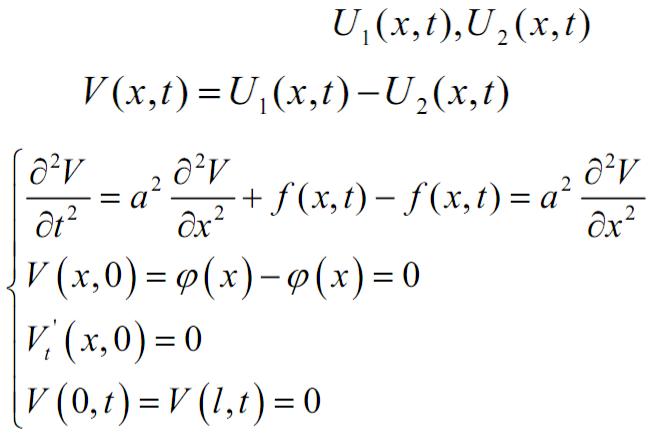
Теорема единственности для уравнения колебаний струны

Доказательство: (от противного)

Пусть есть два решения

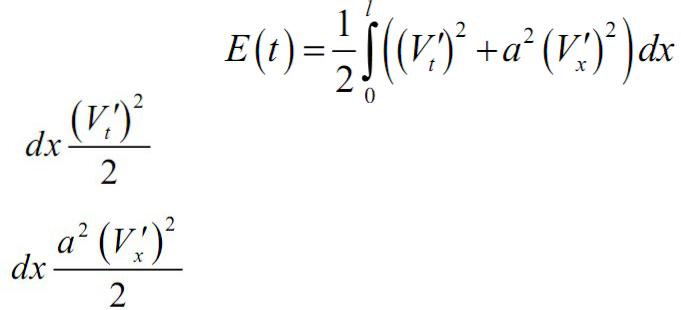
Теорема единственности для уравнения колебаний струны

Физически, теорема единственности доказывается из закона сохранения энергии:

– энергия элементарной части струны (кинетическая энергия);

– энергия элементарной части струны (потенциальная энергия);

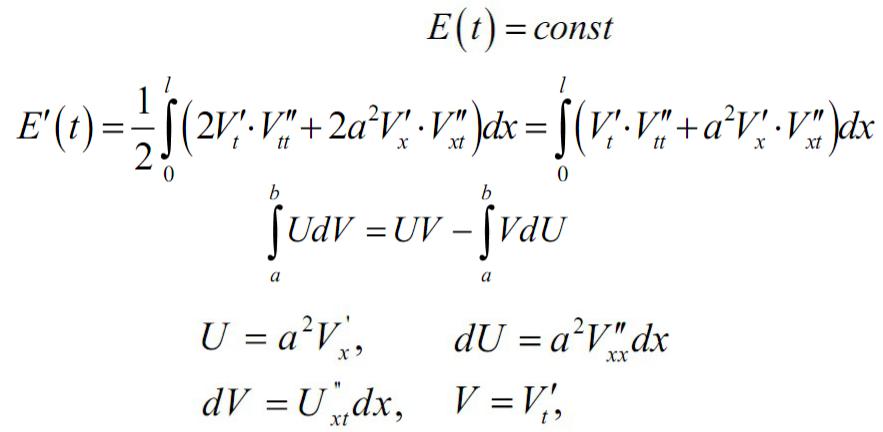
Теорема единственности для уравнения колебаний струны

Докажем, что

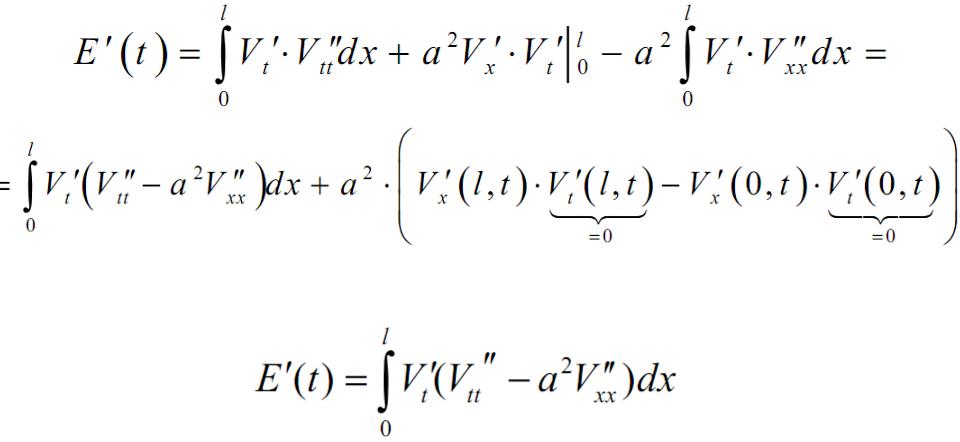
Теорема единственности для уравнения колебаний струны

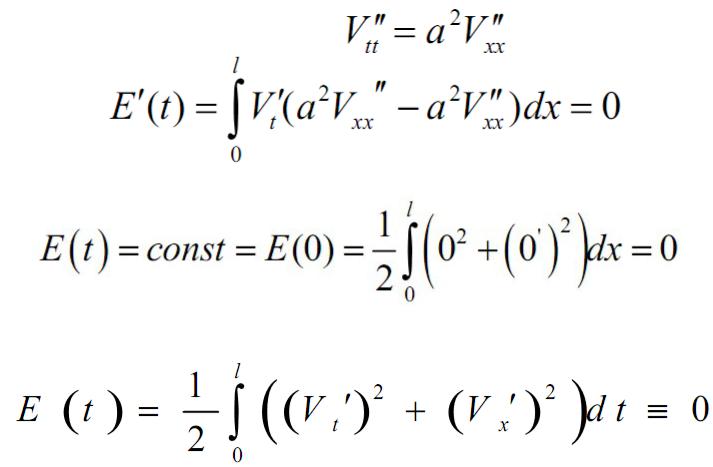
Теорема единственности для уравнения колебаний струны

подставим

Учитывая начальные условия, получаем:

значит, что при любом t:

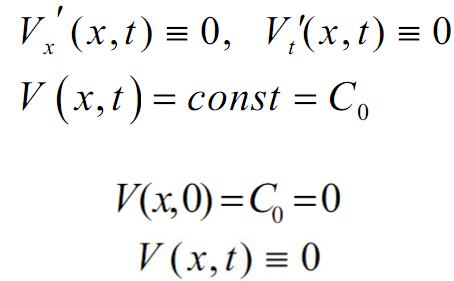
Теорема единственности для уравнения колебаний струны

заключаем, что

Пользуясь начальным условием, находим:

Следовательно, если существуют две функции U1(x,t) и

U2(x,t) удовлетворяющие всем условиям теоремы, то

U1(x,t)≡U2(x,t) .

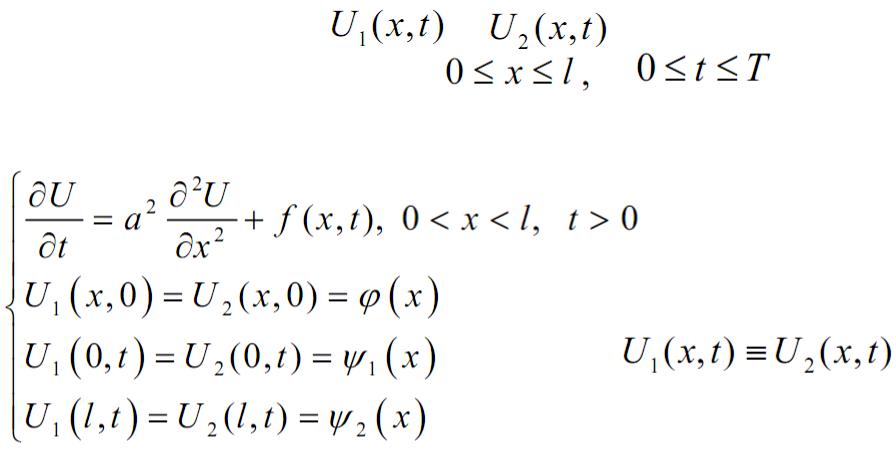
Теорема единственности для уравнения теплопроводности

Если две функции, и определенные и непрерывные в области удовлетворяют уравнению теплопроводности с начальными и краевыми условиями

то

Теорема единственности для уравнения теплопроводности

Рассмотрим функцию