9.3. Обработка результатов косвенных измерений.

Под косвенным измерением понимается определение искомого значения ФВ Y на основании результатов прямых измерений других ФВ x_j, функционально связанных с искомой величиной.

Y  F(х₁, х_2, х₃, , х_j, , х_m), (9-12)

Функция F может обозначать линейную или нелинейную зависимости измеряемой величины Y от аргументов x_j, поэтому косвенные измерения принято делить на косвенные измерения при линейной зависимости и косвенные измерения при нелинейной зависимости F от аргументов x_j. При m=1, т.е. при одном аргументе зависимость (9-12) будет иметь вид Y  F(х) и вычисления результирующей погрешности измерения значительно упрощаются.

Методы обработки результатов косвенных измерений при линейной функции хорошо разработаны. При этом используется подход, основанный на раздельной обработке результатов измерений аргументов x_j и их погрешностей.

Методы обработки результатов косвенных измерений при нелинейной функции сводятся, как правило, к линеаризации зависимости (9-12). При таком подходе делается оценка возможности линейного приближения, а также определяются дополнительные погрешности из-за линеаризации. Используются также метод привидения и реже метод перебора [75].

9.3.1. Основные соотношения при линейной зависимости.

Если функция (9-12) линейна, и её можно представить в виде

, (9-13)

где b_j постоянные коэффициенты, m – число аргументов,

то дисперсия результата измерения может быть определена по формуле:

, (9-14)

где оценка коэффициента корреляции (статистической связи) между погрешностями переменных (аргументов)x_k и x_r, во втором слагаемом,– оценки СКО результатов измерения. В общем случае коэффициентыb_j вычисляются через функции влияния .

Как видно из формулы (9-14), погрешность косвенных измерений может увеличиваться или уменьшаться в зависимости от знака и величины коэффициента корреляции.

Наилучшей оценкой результата косвенных измерений является величина функции F при аргументах, принимаемых среднеарифметическое значение, т.е.:

. (9-15)

Если погрешности измерения аргументов статистически независимы, т.е. коэффициенты корреляции =0, то соотношение (9-14) упрощается и записывается виде:

. (9-16)

При ограниченном числе измерений в соотношениях (9-14) и (9-16) оценки дисперсий определяются по формуле (8-3) табл.8-1.

Доверительные границы случайной погрешности результатов косвенных измерений при числе измерений n>30 и нормальном распределении случайных погрешностей аргументов можно рассчитывать, используя нормальное распределение Гаусса. При меньшем числе измерений для определения доверительного интервала используется распределение Стьюдента, эффективное число степеней свободы которого рассчитывается по приближенной эмпирической формуле: [74]:

, (9-17)

где n_j -число прямых измерений каждого из аргументов величины Q_j, или в общем виде . Для прямых измеренийb_j=1 и число степеней свободы определяется по известному соотношению k = k_эфф = n-1. Формула (9-17) подобна (9-11).

Формулы для суммарной погрешности косвенных измерений подобны формулам (9-3) – (9-5), используемых для прямых измерений. Результат измерения записывается в виде

приР= % (9-18)

Если неисключенная систематическая погрешность составляет 0,8 и менее от случайной СКП результата измерения, то она не учитывается в конечном результате, который должен записываться в виде

(Р) =(Р) =, (9-19)

и наоборот, если неисключенная систематическая погрешность в 8 и более раз превышает СКП результата измерения, то учитывается только систематическая погрешность и доверительная граница записывается в виде (Р) = (Р) (формула (9-4)), где

(9-20)

При 0,8    8 оценку суммарной доверительной границы результата измерения вычисляют по формуле (9-5), где

(9-21)

Коэффициент вычисляют по эмпирической формуле

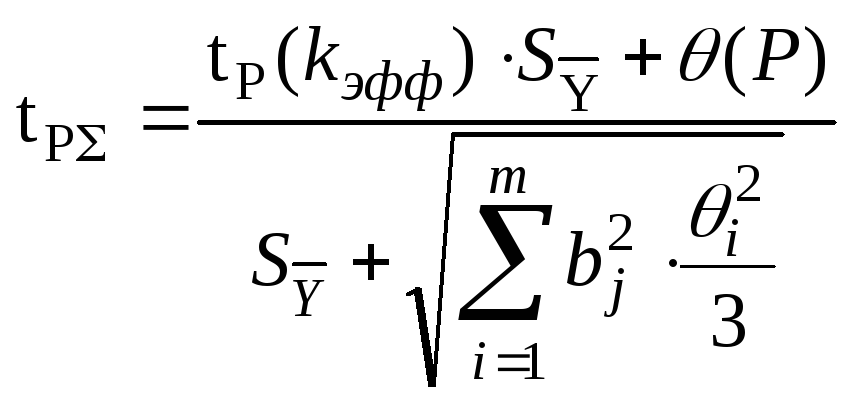, (9-22)

где  (Р) – граница неисключенной составляющей погрешности, определенной по формуле (8-4) или (8-5) при доверительной вероятности Р, t_P (k_эфф) - коэффициент, определенный по таблицам Стьюдента, при той же вероятности Р, k_эфф. – эффективное число степеней свободы, определяемое по формуле (9-17).

Для упрощения вычислений при 0,8    8 может быть использована формула [66,75]: (Р) =, где коэффициент К определяется потаблице

	0,5	0,75	1	2	3	4	5	6	7	8
К0,95	0,81	0,77	0,74	0,71	0,73	0,76	0,78	0,79	0,80	0,81
К0,99	0,87	0,85	0,82	0,80	0,81	0,82	0,83	0,83	0,84	0,85

При отсутствии данных о виде функции распределений составляющих погрешности результат измерения записывают в форме

Пример 9.2. . Определить дисперсию погрешности результата косвенных измерений. Результаты прямых измерений и их погрешности - независимы. Дисперсии результатов измерений аргументов известны и равны ₁, ₂, ₃,..._m.

Решение.

Поскольку коэффициенты влияния то СКО будет равно

При , где— дисперсияj переменной. Результат измерения при доверительной вероятности Р можно записать в виде:

или , где.

В частности при ,. Относительная погрешность, равная, и для разности аргументов может достигать большой величины.