
Sandrakova_Funktsii_mnogikh_peremennykh_2015
.pdfПусть f имеет координатное представление (задано координатными функциями)
y j = f j (x1 ,…, xm ) , j =1, 2,…, n .
Теорема 5.1. Отображение f : G → Rn области G Rm дифференцируемо в точке x G тогда и только тогда, когда в этой точке x дифференцируема каждая функция f j ( x1 ,…, xm ) , j =1, 2,…, n координатного представления отображения f.
Определение 5.5. Непрерывное отображение f : G → Rn облас-
ти G Rm в |
евклидово координатное |
пространство называется |
отображением |
класса Cr на области |
G, если все функции |
f j ( x1 ,…, xm ) = y j , j =1, 2,…, n класса Cr |
на области G. |
|
Определение 5.6. Отображение f : G → Rn называется гладким на G, если j , j =1, 2,…, n f j ( x1 ,…, xm ) класса C∞ на G.
Теперь нас будет интересовать локально обратимое отображение, т.е. такое отображение f : G → Rn , G – область в Rm, чтоU ( x) – окрестность точки x, U ( x) G и такая, что сужение ото-
бражения f на U(x) |
взаимно однозначно, |
т.е. для f : U (x) →V ( y) , |
|||||||||||||
V ( y) = f (U ( x)) – окрестность точки |
|
f (x) = y , и |
обратное ото- |
||||||||||||
бражение f −1 : V ( y) →U ( x) |
|
так, что |
f −1 f = idx |
– |
тождественное |
||||||||||
отображение U(x) на себя ( x U ( x) : idx (x) = x ) и |
f f −1 |
= id f ( x) – |
|||||||||||||
тождественное отображение окрестности |
V ( y) =V ( f ( x)) |
на себя, |
|||||||||||||
т.е. y V ( y) : id f ( x) ( y) = y . |
|
|
|
|
|
|
|
|
|
|
|
|
|||
Теорема 5.2. Пусть |
f : U ( x) →V ( y) , |
y = f ( x) |
– отображение |
||||||||||||
окрестности точки |
x |
на окрестность точки |
y = f ( x) , U ( x) Rm , |
||||||||||||
V ( y) Rn . И пусть f |
непрерывно в точке x |
|
и имеет обратное ото- |
||||||||||||
бражение f −1 : V ( y) →U ( x) , |
и оно непрерывно в точке |
y = f ( x) . |
|||||||||||||
Пусть, кроме того, f |
дифференцируемо в точке x, и касательное ото- |
||||||||||||||
′ |
m |
→Tf ( x) R |
n |
имеет обратное |
|
|
|
||||||||
бражение f (x) : Tx R |
|
|
|
|
|
||||||||||
|
|
′ |
−1 |
: Tf ( x) R |
n |
→Tx R |
m |
. |
|
|
|
||||
|
|
[ f (x)] |
|
|
|
|
|
||||||||
51

Тогда отображение f–1 дифференцируемо в точке y = f (x) , и справедливо равенство ( f −1 )′( y) =[ f ′(x)]−1 .
Таким образом, из этой теоремы следует, что взаимно обратные дифференцируемые отображения имеют в соответствующих точках взаимно обратные касательные отображения.
Прежде чем приступать к примерам, рассмотрим ещё несколько определений, связанных с отображениями.
Определение 5.7. Пусть f : G → D , где G – область в Rm, D – об-
ласть в Rn. Отображение f называется гомеоморфизмом, если f взаимно однозначноеотображениеи f, f –1 непрерывнынаG иD соответственно.
Определение 5.8. Отображение f : G → Rn , G – область в Rm,
m ≤ n , называется локальным гомеоморфизмом, если у каждой точки x G существуетокрестность U (x) G , накоторойf гомеоморфизм.
Определение 5.9. Гладкое отображение f : Rm → Rn называет-
ся |
погружением, |
если |
для каждой точки x Rm отображение |
|||
′ |
|
m |
→Tf ( x) R |
n |
является изоморфизмом линейных про- |
|
f (x) : Tx R |
|
|
||||
странств Tx Rm и f ′(x)(Tx Rm ) Tf ( x) Rn .
Определение 5.10. Погружение f называется вложением, если оно является гомеоморфизмом на свой образ.
Пусть гладкое отображение f : Rm → Rn представляется в координатах системой функций y j = f j (x1 ,…, xm ) , j =1, 2,…,n , и все
функции гладкие, т.е. класса C∞ на Rm. Составим матрицу Якоби этой системы функций
∂f 1
∂x1 Af j =
∂f n∂x1
В каждой фиксированной точке
∂f 1 ∂xm .
∂f n ∂xm
x Rm получаем числовую мат-
|
1 |
|
|
|
|
рицу размера n ×m . Если записывать векторы h = h |
|
|
T Rm |
по |
|
|
|
|
|
x |
|
|
|
m |
|
|
|
h |
|
|
|
|
|
52
столбцам в некотором фиксированном базисе, связанном с выбранной системой координат (x1 ,…, xm ) , то Af j ( x) – линейный оператор,
действующий из T Rm |
в T |
f ( x) |
Rn |
обычным образом: |
||||||||
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
∂f 1 |
|
k |
|
|
|
|
|
|
|
|
|
∑ |
|
|
h |
|
|
|
|
|
|
|
|
∂x |
k |
|
|
|
||||
|
|
|
|
k =1 |
|
|
|
|
Tf ( x) |
Rn . |
||
A |
j |
|
h = |
|
|
|
|
|
|
|||
f |
|
( x) |
|
m |
∂f n |
|
k |
|
|
|
||
|
|
|
|
|
∑ |
|
k |
h |
|
|
|
|
|
|
|
|
|
∂x |
|
|
|
|
|||
|
|
|
|
k =1 |
|
|
|
|
|
|
||
Теорема 5.3. Гладкое отображение f : Rm → Rn является погружением тогда и только тогда, когда rang Af j = m .
Рассмотрим свойства некоторых отображений f в следующих примерах.
Пример 5.1. Даны пространства R1 с координатой x, R2 с координатами ( y1 , y2 ) ; f : R1 → R2 и пусть f представлено координатными функциями:
y1 = f 1 (x) = x2 ; y2 = f 2 (x) = x3 .
Решение. Это отображение гладкое, так как х2, х3 – многочлены.
Касательное отображение или дифференциал |
df (x) задаётся сис- |
|||||||||
темой функций (df (x))1 = 2x , |
(df (x))2 = 3x2 , |
x R1 . |
||||||||
Является ли данное отображение погружением? |
||||||||||
Составим матрицу Якоби |
|
|
|
|||||||
|
|
|
∂f |
1 |
|
|
|
|
|
|
|
Af j ( x) |
|
|
|
2x |
|
|
|||
|
= |
∂x2 |
|
= |
3x |
2 |
. |
|
||
|
|
|
∂f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂x |
|
|
|
|
|
|||
Если |
x ≠ 0 , |
то |
rang Af j ( x) =1 , если |
|
||||||
х = 0, то |
rang Af j ( x) |
= 0 , следовательно, |
|
|||||||
это отображение не является погруже- |
|
|||||||||
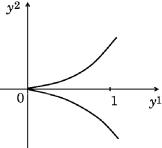
нием. Образ прямой R1 при отображе- |
|
|||||||||
нии f на плоскости |
R2 ( y1 , y2 ) является |
|
||||||||
полукубической параболой (рис. 5.1), x |
Рис. 5.1 |
|||||||||
53
выступает в роли параметра. Отображение f является взаимно однозначным отображением R1 на f(R1).
Пример 5.2. Пусть f : R1 → R2 , R1 (x) , R2 ( y1 , y2 ) , и в координатах f представляет система координатных функций:
y1 = f 1 (x) = x2 ; y2 = f 2 (x) = x3 − x .
Решение. Это дифференцируемое отображение в каждой точке x R1 , так как оно представлено многочленами:
2x |
|
= Af j ( x) . |
||
df (x) = |
3x |
2 |
|
|
|
|
−1 |
|
|
rang Af j ( x) =1 в каждой точке x R1 . Следовательно, согласно тео-
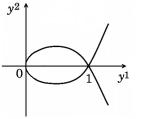
реме 5.3 это – погружение. Но это отображение не является взаимно однозначным. Точки xˆ = −1 и x =1 переходят при этом отображении в одну точку y0 = (1, 0) . Образ R1 при отображении показан
на рис. 5.2.
Отображение f является локальным гомеоморфизмом, так как согласно теореме о неявных функциях система уравнений
y1 − x2 = 0;
y2 − x( x2 −1) = 0,
где на три независимые переменные накладывается две связи при условии, что rang Af j ( x) =1 , для всех x R1 может быть локально
разрешима, что устанавливает взаимно однозначное гладкое ото-
бражение |
некоторой |
окрестности U (x) Rx1 на |
f (U (x)) =V ( y) , |
|||
y = f (x) , |
V ( y) R2 |
(V ( y) – окрестность точки |
y |
на |
f (R1 ) ). |
|
|
|
Возьмем точку x =1 . |
|
|
|
x |
|
|
У неё существует |
||||
|
|
окрестность U (x) R1 |
(рис. |
5.3), |
такая, |
|
|
|
что f устанавливает взаимно однозначное |
||||
|
|
отображение множеств U (x) |
и f (U (x)) . |
|||
|
|
Следовательно, отображение f является |
||||
|
|
погружением, но не является вложением. |
||||
|
|
(Склеились две далекие точки x и xˆ .) |
||||
Рис. 5.2
54
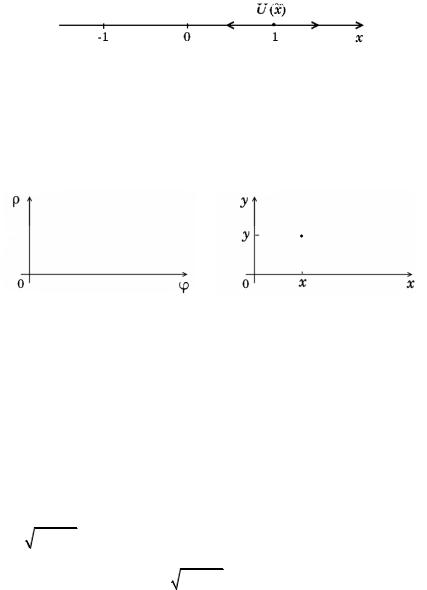
Рис. 5.3
Пример 5.3. Пусть f : Rϕρ2 → Rxy2 , где Rϕρ2 и Rxy2 – это два экзем-
пляра R2 с декартовыми координатами (ϕ, ρ) и (x, y) (рис. 5.4), и отображение f представляется формулами:
x = ρcos ϕ; |
ρ (−∞, +∞) , ϕ (−∞, +∞) . |
f : |
|
y = ρsin ϕ; |
|
Рис. 5.4
Ответим на следующие вопросы:
1)задано ли f на всем Rϕρ2 ;
2)отображает ли f Rϕρ2 «на» Rxy2 или Rϕρ2 «в» Rxy2 ;
3)является ли это отображение дифференцируемым в каждой точке (ϕ, ρ);
4)является ли это отображение погружением?
Решение. 1. Отображение f определено на всей плоскости Rϕρ2 . 2. Докажем, что отображение f является отображением «на».
Возьмем произвольную |
точку |
(x, y) Rxy2 . Пусть x ≠ 0 . Тогда |
|||||||
ρ= x2 + y2 , ϕ = arctg |
y |
, и |
|
|
|
|
|
||
x |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||
|
|
|
y |
|
2 |
|
2 |
|
f |
arctg |
|
|
, x |
|
+ y |
|
|
→(x, y). |
|
|
x |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
55
Если выбрали (0, y), то
π |
|
f |
|
, y |
→(0, y) , т.е. ρ = y. |
2 |
|
|
3. Исследуем отображение f на дифференцируемость; f представляется системой функций:
x= f 1 (ϕ,ρ) = ρcosϕ ;
y= f 2 (ϕ,ρ) = ρsin ϕ;
f 1 (ϕ, ρ) и f 2 (ϕ,ρ) – линейные функции от переменного ρ, и тригонометрические функции sinϕ и cosϕ – дифференцируемые функции переменного ϕ. Функции f 1 (ϕ, ρ) и f 2 (ϕ,ρ) дифферен-
цируемы в каждой точке плоскости (ϕ, ρ). Найдем касательное отображение df (ϕ,ρ)
df (ϕ,ρ) : T |
ρ) |
R2 →T |
R2 ; |
(ϕ, |
( x, y) |
|
|
x = f 1 (ϕ,ρ) , |
|
y = f 2 (ϕ,ρ) . |
|
Линейное отображение df в точке (ϕ, ρ) задается матрицей Яко-
би системы функций |
f 1 (ϕ, ρ) , f 2 (ϕ,ρ) |
|
||||||||||||
|
|
|
|
∂f 1 |
|
|
∂f 1 |
|
|
|
|
|
|
|
A |
|
|
|
∂ϕ |
|
|
∂ρ |
|
|
−ρsin ϕ |
cos ϕ |
|||
j |
|
= |
∂f 2 |
|
|
∂f 2 |
= |
|
ρcosϕ |
. |
||||
f |
|
(ϕ,ρ) |
|
|
|
|
|
sin ϕ |
||||||
|
|
|
|
∂ϕ |
|
|
∂ρ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
4. Является ли это отображение погружением f ? Вычислим |
||||||||||||||
|
|
det A |
j |
|
= |
|
−ρsin ϕ |
cos ϕ |
|
= −ρ. |
||||
|
|
|
|
|
||||||||||
|
|
|
f |
|
(ϕ,ρ) |
|
|
ρcos ϕ |
|
sin ϕ |
|
|
|
|
При ρ ≠ 0 rang Af |
j (ϕ,ρ) = 2 |
при всех ϕ. При ρ = 0 rang Af j (ϕ,ρ) =1 |
||||||||||||
при всех ϕ. Следовательно, согласно теореме 5.3 это отображение не является погружением.
Постараемся разобраться, как осуществляется это отображение. Так как sinϕ и cosϕ есть 2π-периодические функции, то точки (ϕ0 + 2πn,ρ) при ρ ≠ 0 переходят в одну и ту же точку плоскости
(x, y) =(ρcosϕ0 ,ρsin ϕ0 ) (ρ фиксировано). И все точки оси ϕ: ρ = 0
56
переходят в точку (0, 0) Rx2, y . Следовательно, отображение f не
является взаимно однозначным.
Но остается непонятным следующий факт: склеиваются точки (ϕ0 + 2πn,ρ) , ρ ≠ 0, n Z , а ранг матрицы Якоби остается равным
2, а при склеивании между собой точек (ϕ, 0), где ϕ произвольно, f : (ϕ,0) →(0,0) ,
ранг матрицы Якоби становится равным 1. Во всех этих точках матрица Якоби вырождается.
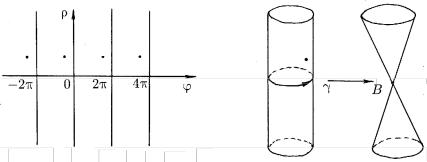
Будем осуществлять отображение f постепенно. Сначала, ис-
пользуя периодичность sinϕ и cosϕ, |
из плоскости R2 |
склеим ци- |
|
|
|
ϕ,ρ |
|
линдр. Для этого разделим |
R2 |
на вертикальные полосы |
|
|
ϕ,ρ |
|
|
τn ={(ϕ,ρ), ϕ [2πn, 2π(n +1)], |
ρ (−∞, +∞) , n Z } (рис. 5.5). |
||
Рис. 5.5
Одна полоса наклеивается на другую, и края полосы склеиваются между собой.
На полученном цилиндре выделяется окружность γ, являющаяся образом оси ϕ при этом промежуточном отображении. Затем, учитывая, что все точки вида (ϕ,0) → γ →(0,0) , мы затянем «талию» γ в точку B. Получается «хлопушка» с одним концом. Потом, поместив точку B на плоскости Rxy2 в начале координат, верхнюю часть
«хлопушки» – над Rxy2 , а нижнюю – под плоскостью Rxy2 , мы начнем аккуратно наклеивать «хлопушку» на плоскость Rxy2 . При этом
57
нижнюю часть «хлопушки» надо предварительно повернуть на 180° против часовой стрелки, и только после этого аккуратно взаимно однозначно наклеивать на плоскость Rxy2 . Это происходит
потому, что полуполоса
|
|
π |
|
|
τn |
(ϕ,ρ), |
ϕ 2πn, |
2 |
+ 2πn |
, ρ [0, + ∞) |
|
|
|
|
|
|
отображается в первый квадрант плоскости Rxy2 : x ≥ 0, y ≥ 0, и в него же отображение f переводит кусок
|
|
3 |
|
|
|
|
(ϕ,ρ), ϕ π+ 2πn, |
|
π+ 2πn |
, ρ (−∞,0] |
τn . |
||
2 |
||||||
|
|
|
|
|
||
Аналогично со всеми остальными кусками полосы τn, n Z. Мы получили отображение f. При этом поняли, что в каждую
точку плоскости Rxy2 (кроме точки O(0, 0)) отображается счетное множество точек плоскости Rϕρ2 , причем счетное множество точек из верхних полуполос τ+n : ρ > 0 , n Z, и счетное множество точек из нижних полуполос τ−n : ρ < 0 , n Z.
Но каждая из этих точек (ϕ,ρ) , ρ ≠ 0 является точкой локальной гомеоморфности отображения f. Для понимания этого доста-
точно у |
каждой такой точки (ϕ,ρ) , |
ρ ≠ 0 , взять |
δ-окрестность |
||||||
Uδ (ϕ,ρ) , |
ρ ≠ 0 , где |
|
|
ρ |
|
, |
π |
. Эта Uδ (ϕ,ρ) |
не пересечет |
|
|
||||||||
0 < δ < min |
|
|
|
||||||
|
|
|
|
|
|
|
2 |
|
|
оси ϕ, и в нее не попадут точки, которые f склеивает из-за периодичности cosϕ, sinϕ. Следовательно, f гомеоморфно отображает
Uδ (ϕ,ρ) , ρ ≠ 0 → f (Uδ (ϕ,ρ))
(на свой образ). А с точками оси ϕ дело обстоит совсем не так. Все точки оси ϕ переходят при отображении f в одну точку O(0, 0).
Возьмем произвольную точку оси ϕ, (ϕ, 0) (рис. 5.6).
58
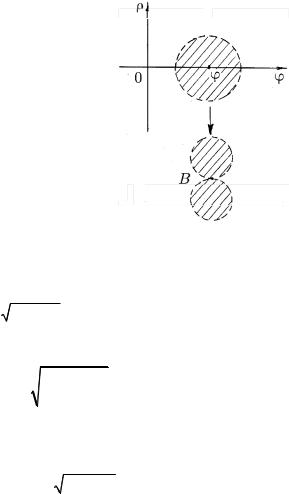
Какую бы окрестность Uε (ϕ,0) ни |
|
|
взять, f не является на ней взаимно од- |
|
|
нозначным. Более того, если Uε (ϕ,0) – |
|
|
сферическая окрестность точки (ϕ,0) , |
|
|
то диаметр этой окрестности стягивает- |
|
|
ся в точку, и окрестность не переходит |
|
|
вообще в окрестность точки. О таких |
|
|
точках говорят, что в них нарушается |
|
|
регулярность отображения, т.е. нару- |
|
|
шается локальный гомеоморфизм. Для |
|
|
многих задач это плохо. |
|
|
Пример 5.4. |
Рассмотреть свойства |
|
отображения f : |
Dn → Rn , где Dn – от- |
Рис. 5.6 |
крытый шар в |
Rn (x1 ,…, xn ) , |
т.е. Dn : |
|
(x1 )2 +…+ (xn )2 <1 , и ото- |
||||||||
бражение f представляется формулами |
|
|
||||||||||
|
|
|
f : x → |
|
|
x |
|
= y ; |
x Dn , y Rn , |
|||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
1 −(x, x) |
|
|
|||
или в координатах |
|
|
|
|
|
|
|
|||||
|
j |
|
j |
1 |
|
n |
|
|
|
x j |
|
; j =1, 2,…,n . |
y |
|
= f |
|
(x ,…, x |
|
) = |
|
|
|
|
||
|
|
|
|
|
|
|
||||||
n
1− ∑(xk )2
k =1
Решение. Отображение f задано гладкими функциями на Dn.
Обратное отображение f −1 : Rn → Dn |
задается формулами |
|||
f −1 : y → |
|
y |
|
= x Dn . |
|
|
|
||
1 |
+( y, y) |
|||
Значит, f и f–1 – гладкие гомеоморфизмы. Следовательно, Dn и Rn диффеоморфны.
Пример 5.5. Пусть f : Rxn → Ryn (т.е. m = n N ) и f представлено формулами
y j = f j (x1 ,…, xn ) ; j =1, 2,…,n ,
59

где j , j =1, 2,…,n , f j (x1 ,…, xn ) дифференцируема в |
точке |
||||
x = (x1 ,…, xn ) . Найти дифференциал отображения f в точке x. |
|
||||
|
1 |
|
|
|
|
Решение. Рассмотрим вектор смещения |
h = h |
|
|
T Rn |
и вы- |
|
|
|
|
x |
|
|
|
n |
|
|
|
|
h |
|
|
|
|
званный этим вектором смещения вектор приращения отображения f (x,h) = f (x + h) − f (x) .
Так |
как |
f |
дифференцируемо |
в |
точке |
x, |
то |
|
f (x,h) = L(x)h +ω(x,h), где L(x) : T Rn →T |
f ( x) |
Rn , L(x) |
– линей- |
|||||
|
|
|
x |
|
|
|
|
|
ное отображение, заданное на касательном пространстве |
T Rn |
век- |
||||||
|
|
|
|
|
|
|
x |
|
торов смещения, а ω(x, h) = o(
 h
h
 ) при
) при 
 h
h
 → 0 . Запишем все в координатах
→ 0 . Запишем все в координатах
|
( f (x, h)) j = (L(x)) j h +ωj (x, h) ; j =1, 2,…,n . |
|
|
|
Для j , |
j =1, 2,…,n ; (L(x)) j h – это линейная числовая функция |
|||
(линейный |
функционал) аргумента h в линейном пространстве |
|||
T Rn , т.е. |
L(x) является линейным оператором |
T Rn →T |
f ( x) |
Rn . |
x |
|
x |
|
|
Это дифференциал отображения f в точке x, т.е. df(x) |
′ |
|
|
|
(или f (x) ), и |
||||
он, как линейный оператор, может быть представлен квадратной матрицей A = (aij ) , матрицей Якоби системы функций ( f (x)) j , где
|
|
j |
|
|
|
|
|
|
∂( f (x)) j |
|||||||||||||||
ai |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; i, j =1,2,…, n , |
||||||||
|
|
|
|
∂xi |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и при этом ωj (x, h) = o( |
|
|
|
|
h |
|
|
|
) при |
|
|
|
h |
|
|
|
→ 0 , т.е. |
|||||||
|
|
|
|
|
|
|
|
|||||||||||||||||
|
lim |
ωj (x1 ,…, xn , h1 ,…, hn ) |
= 0 |
|||||||||||||||||||||
|
|
|||||||||||||||||||||||
|
h |
→0 |
|
|
|
|
|
n |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∑(hk )2 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k =1 |
||||||||||
при фиксированном x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
60
