KR_dlya_ekzamena (1)

КР1. Курс «Моделирование макроэкономических процессов и систем»

Производственная функция.

Группа ___________________ Студент ________________________________

1. Производственная функция это выражение связи между объемом затраченных ресурсов, параметрами технологии, результатами производства и объемами выпуска.

2. Вид двухфакторной производственной функции Кобба-Дугласа Y=aK^αL^β

Вид линейной двухфакторной производственной функции Y=aK+bL

3. Вывести уравнение изокванты для ПФ из п.2. для объемов выпуска 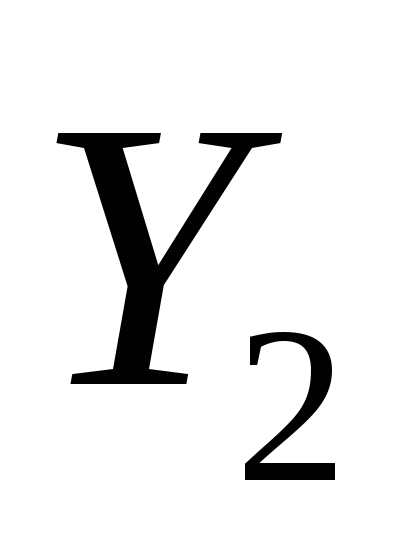и .

Для ПФ Кобба-Дугласа: и

Для линейной ПФ: K₂ = (Y₂-bL₂)/a и K₃ = (Y₃-bL₃)/a

Нарисовать изокванту для объема выпуска и изокванту для объема выпуска :

Изокванта Кобба-Дугласа: Линейная изокванта:

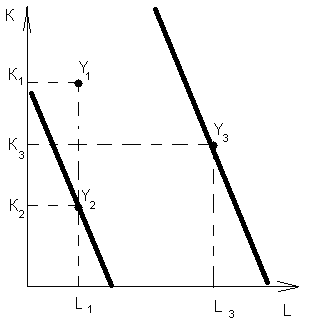
Внимание! Вы можете нарисовать изокванты так, чтобы на одну из них попадала точка Y₁, главное, чтобы они были параллельны друг другу! Обратите внимание на то, какой вид производственной функции (ПФ) вам дан: Кобба-Дугласа или линейный.

4. Для производственной функции из в.3 сравнить объем выпуска (больше, меньше или равен)

Ответ зависит от варианта, но правила следующие: а) если Ya лежит на одной изокванте с Yb, то Ya=Yb

б) если Ya лежит выше изокванты, на которой расположен Yb, то Ya>Yb

в) если Ya лежит ниже изокванты, на которой расположен Yb, то Ya<Yb

Определяйте по своему графику из пункта 3.

КР 2. Курс «Моделирование макроэкономических процессов и систем»

Сектор производства .

Группа ___________________ Студент ________________________________

Для производственной функции вида f(x)=ax²+bx+c, цены w на фактор производства x и цены готовой продукции p:

1. Функция прибыли имеет следующий вид:

y*p – x*w = p(ax²+bx+c) – xw

2. Выписать условие первого порядка максимизации функции прибыли:

∂ = ∂(yp – xw) = ∂(p(ax²+bx+c) – xw) = 2apx+b-w

∂x ∂x ∂x

3. Найти функцию спроса на факторы производства:

(w-b)/2ap

4. Найти спрос на фактор производства подставляем в формулу из п.3 числа из варианта

5. Найти объем выпуска y=f(x)= подставляем полученное значение х из п.4 в начальную формулу f(x) из условия

6. Найти максимальную прибыль подставляем полученное значение х из п.4 в формулу из п.1

*п.1-3 в общем виде

КР 3 Модель Солоу.

Группа ____________ Студент ________________________________

Для заданной производственной функции Y(t) темпа прироста населения , нормы сбережений s, и А(0)=1,

1. Вывести производственную функцию в интенсивной форме:

y(t) = k^α(t) => Y(t)/(A(t)L(t)) = [K(t)/(A(t)L(t))]^α

2. Выписать условие стационарного состояния экономики:

Sf(k) – k(η+g+δ) = 0

3. Найти значение капиталловооруженности в стационарном состоянии:

[( η+g+δ)/S]^1/(α-1)

4. Для указанного в варианте момента времени t найти численность населения:

L(t) = L(0)e^ηt

Подставляем значения переменных из варианта и получаем ответ.

5. Для указанного в варианте момента времени t найти объем капитала в модели:

K(t)=k^*A(t)L(t) = k^*A(0)e^gtL(0)e^ηt = k^*A(0)L(0)e^(g+η)t

Подставляем значения переменных из варианта и значение k^* из пункта 3 и получаем ответ.

(Решение задачи привести на обратной стороне листа)

КР 5. Курс «Моделирование макроэкономических процессов и систем»

Поведение потребителя.

Группа ____________ Студент ________________________________

Для заданной функции полезности U(X,Y), цены на товар X - P_x, на товар Y - P_y и доходе I

1. Целевая функция потребителя:

U(X,Y) → max_{x,y}

2. Ограничение потребителя:

Px * X + Py * Y ≤ I

3. Выписать задачу, которую должен решить потребитель:

U(X,Y) → max_{x,y}

s.t. Px * X + Py * Y ≤ I

4. Найти оптимальный объем товара как функцию от P_x, P_y ,I. Х= (I – Py * Y)/Px

5. Найти оптимальный объем товара как функцию от P_x, P_y ,I. Y= (I – Px *X)/Py

6. Найти полезность, получаемую потребителем от данного набора благ

U(X,Y)= расчет смотри ниже

(Решение задачи привести на обратной стороне опросного листа)

Решение:

Решаем методом Лагранжа. Строим Лангранжан (L):

L(XYλ) = U(X,Y) - λ(Px * X + Py * Y - I)

∂ L(XYλ) = 0

∂X

∂ L(XYλ) = 0 (X^* Y^*) – при которых U(X^* Y^*) = max

∂Y

∂ L(XYλ) = 0

∂λ

Подставляем значения из варианта. Находим производные, у нас получается система из трех уравнений с тремя неизвестными. Решаем ее. Полученные X и Y записываем в ответ.

КР 6. Модель Даймонда.

Группа ____________ Студент ________________________________

Для функции мгновенной полезности u(c), (CRRA) c параметром , фактором дисконтирования . Доход w₁ в первом периоде и w₂ во втором периоде.

1. Задача индивида заключается в том, чтобы так распределить доходы в первом и втором периоде, чтобы оптимизировать удовлетворение индивида от жизни.

2. Выписать целевую функцию индивида:

U(C₁C₂) = U(C₁) + βU(C₂) → max_{С1C2}

3. Выписать бюджетное ограничение индивида:

w₁ + w₂/(1+r) ≥ C₁ + C₂/(1+r)

4. Найти оптимальный объем потребления индивида в первом и втором периоде:

C₁^* = расчет смотри ниже

C₂^* = расчет смотри ниже

(Решение задачи привести на обратной стороне листа)

Решение: Решаем методом Лагранжа. Строим Лангранжан (L):

L(C₁C₂λ) = U(C₁) + βU(C₂) + λ(C₁ + C₂/(1+r) – (w₁ + w₂/(1+r)))

L(C₁C₂λ) = (C₁^1-γ)/(1-γ) + β(C₂^1-γ)/(1-γ) + λ(C₁ + C₂/(1+r) – (w₁ + w₂/(1+r)))

∂ L(C₁C₂λ) = C₁^-γ + λ = 0

∂C₁

∂ L(C₁C₂λ) = βC₂^-γ + λ/(1+r) = 0 (C₁^* C₂^*) – при которых U(C₁^* C₂^*) = max

∂C₂

∂ L(C₁C₂λ) = C₁ + C₂/(1+r) - w₁ - w₂/(1+r) = 0

∂λ

C₁^-γ – (1+r)βγ^-γ = 0

C₁ = β(1+r) C₂

C₁ + C₂/(1+r) = w₁ + w₂/(1+r)

C₂ (β(1+r))^1/γ + C₂/(1+r) = w₁ + w₂/(1+r)

C₁^* = (w₁ + w₂/(1+r)) (β(1+r))^1/γ Подставляем числа согласно своему

(β(1+r))^1/γ + 1/(1+r) варианту, ответ заносим в пункт 4

C₂^* = w₁ + w₂/(1+r)____ Подставляем числа согласно своему

(β(1+r))^1/γ + 1/(1+r) варианту, ответ заносим в пункт 4

Термины:

W – доход

С – трата

γ – показатель готовности индивида к межвременному замещению

β – фактор дисконтирования

r – процентная ставка по сбережениям (при подставлении значения в формулу разделите данное в варианте значение на 100!)