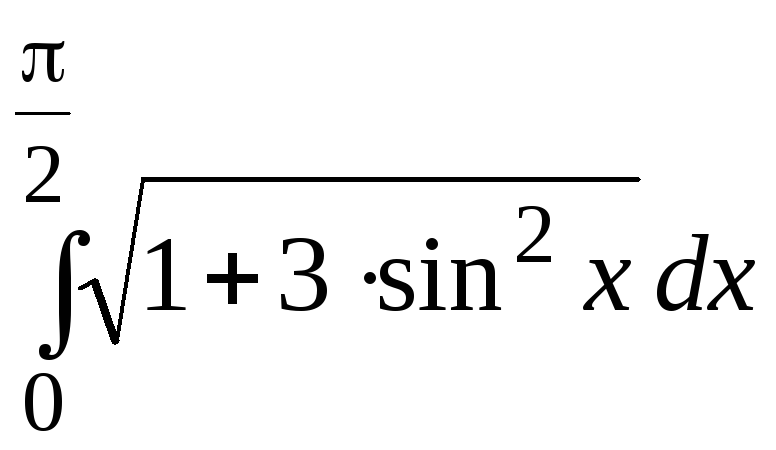Лабораторная работа №7 Вычисление определенного интеграла по методам прямоугольников, трапеций, Симпсона.
(4 часа)
Цель: сформировать у студентов умение вычислять определенные интегралы по методам прямоугольников, трапеций, Симпсона. Оценка погрешностей интегрирования с помощью современных программныех средств.
Задание:
1.Вычислить
по формуле Симпсона определенный
интеграл от функции
с шагом
и шагом
.
Расчеты производить с точностью
.
Оценить абсолютную погрешность по
правилу Рунге. Ответ дать с учетом
поправки Рунге.
2. Вычислить определенный интеграл методами прямоугольников и трапеций.
В таблицах 8 и 9 приведены варианты индивидуальных заданий.
Таблица 8 Варианты задания 1
|
№ Вар |
Задание |
№ Вар |
Задание | |
|
1 |
|
9 |
| |
|
2 |
|
10 |
| |
|
3 |
|
11 |
| |
|
4 |
|
12 |
| |
|
5 |
|
13 |
| |
|
6 |
|
14 |
| |
|
7 |
|
15 |
| |
|
8 |
|
16 |
| |
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
Таблица 9 Варианты задания 2
|
№ Вар. |
Задание |
№ Вар. |
Задание |
|
1 |
|
9 |
|
|
2 |
|
10 |
|
|
3 |
|
11 |
|
|
4 |
|
12 |
|
|
5 |
|
13 |
|
|
6 |
|
14 |
|
|
7 |
|
15 |
|
|
8 |
|
16 |
|
Контрольные вопросы:
Сформулируйте задачу приближенного интегрирования.
Дайте понятие квадратурной формулы.
Вычисление определенных интегралов с помощью формулы прямоугольников. Погрешности численного интегрирования.
Вычисление определенных интегралов с помощью формулы трапеций. Погрешности численного интегрирования.
Вычисление определенных интегралов с помощью формулы Симпсона. Погрешности численного интегрирования.
Запишите формулу прямоугольников. Как оценивается погрешность этой формулы?
Запишите формулу трапеций. Как оценивается погрешность этой формулы?
Запишите формулу Симпсона. Как оценивается погрешность этой формулы?
Лабораторная работа №8 Решение задачи Коши для дифференциальных уравнений первого порядка методом Эйлера
(2 часа)
Цель: сформировать у студентов умение решать задачу Коши для дифференциальных уравнений первого порядка, используя современные программные средства.
Задание: Решить задачу Коши для дифференциальных уравнений первого порядка методом Эйлера.
В таблице 10 приведены варианты задания.
Таблица 10 Варианты задания
|
№ Вар. |
Уравнение |
Нач. точка (x, y) |
Интер. [a;b] |
Шаг |
Решение |
|
1 |
|
(1,e) |
[1;2] |
0.1 |
|
|
2 |
|
(1,2) |
[1;2] |
0.1 |
|
|
3 |
|
(1,0) |
[1;2] |
0.1 |
|
Окончание таблицы 10
|
4 |
|
(0,1/3) |
[1;2] |
0.1 |
|
|
5 |
|
(0,1) |
[0;1] |
0.1 |
|
|
6 |
|
(0,2) |
[0;1] |
0.1 |
|
|
7 |
|
(0,3) |
[0;1/2] |
0.1 |
|
|
8 |
|
(0,2) |
[0;1] |
0.1 |
|
|
9 |
|
(1,1) |
[1;2] |
0.1 |
|
|
10 |
|
(0,1) |
[0;0,5] |
0.05 |
|
|
11 |
|
(0,-2) |
[0;1] |
0.1 |
|
|
12 |
|
(1, 0) |
[1;2] |
0.1 |
|
|
13 |
|
(0,1) |
[0;1] |
0.1 |
|
|
14 |
|
(1,1/e) |
[1;2] |
0.1 |
|
|
15 |
|
(0,0) |
[0;1] |
0.1 |
|
