Metod_MR_sam_rab_Teoret._mekhan._14.03.01_00.00.00

Рисунок 27 – Вращение твердого тела вокруг неподвижной оси

соответствует положительному направлению отсчёта угла поворота ϕ. Модули угловой скорости и углового ускорения равны:

Угловая скорость ω, рад/с, и частота вращения тела n, об/мин, связаны зависимостью:

ω = π n . 30

Скорость точки М тела, отстоящей от оси вращения на расстоянии О1М=h (рис. 27), вычисляется по формуле:

41

Ускорение этой точки равно векторной сумме касательного и нормального ускорений (рис. 27), т.е.:

а = аτ + аn .

Модули ускорений определяются следующим образом:

При рассмотрении передаточных механизмов следует учесть, что, если два колеса находятся в зацеплении, скорость общей точки зацепления (контакта) каждого колеса одна и та же. Это же справедливо и для реечного зацепления зубчатой рейки с зубчатым колесом. В случае, когда два колеса связаны ремённой передачей скорости всех точек ремня и точек, лежащих на ободах этих колёс, также одинаковы; при этом считается, что ремень по ободу колеса не проскальзывает.

Пример 1. Груз 1 движется по закону x = 5 + 40t 2 . Определить скорость, касательное, нормальное и полное ускорения точки М механизма в момент времени, когда путь S, пройденный грузом, равен

10 см, если R2= =30см, r2 = 10 см, R3 = 20 см, r3 = 12 см (рис. 28), где x

– в см, t – в с.

План решения задачи

1)Найти момент времени t1, в который путь, пройденный грузом 1, будет равен S.

2)Определить в виде функций от времени следующие величины:

– скорость груза 1;

– угловую скорость колеса 2;

– угловую скорость и угловое ускорение колеса 3.

3)Вычислить значение угловой скорости и углового ускорения колеса 3 для момента времени t = t1;

42

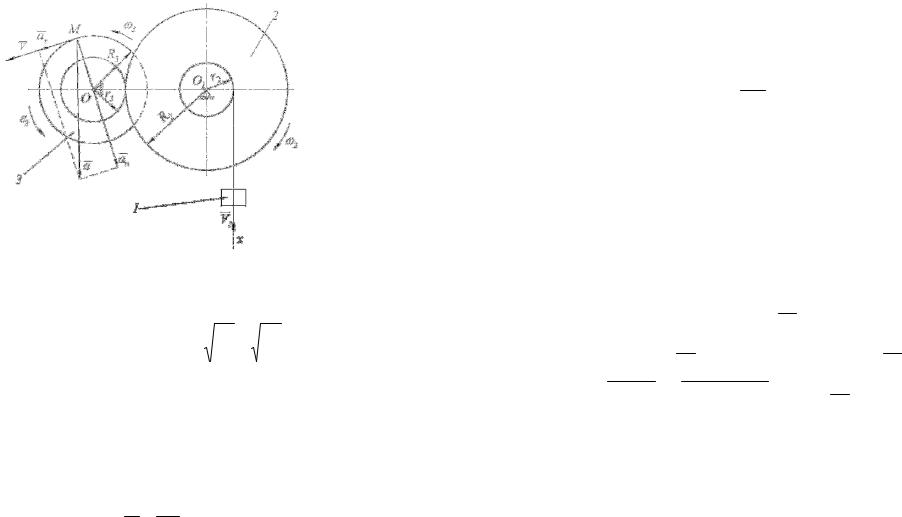
4) По формулам (30), (31) определить скорость, касательное, нормальное и полное ускорения точки М.

Рисунок 28 – К примеру 1.

Решение: Находим момент времени t1, когда S = 10 см:

Определяем скорость груза 1:

V1 = x& = 80t.

Далее находим угловую скорость колеса 2, исходя из нерастяжимости нити и, следовательно, равенстве скорости груза 1 и

точки на ободе колеса 2 радиуса r2, т.е. V1 = ω2r2 . Тогда:

ω2 = V1 = 80t = 8t. r2 10

Направление угловой скорости соответствует направлению скорости груза 1 (рис. 28).

Считаем, что колёса 2 и 3 находятся в зацеплении без проскальзывания. Следовательно, скорость общей точки колёс одинакова, т.е.:

43

ω3 r3 = ω2 R2 .

Откуда определяем угловую скорость и угловое ускорение колеса 3:

ε3 = ω&3 = 20 радс2 .

Вмомент времени t1 = 0,5 с:

показано на рисунке 2.2. Угловое ускорение ε3 направлено по угловой скорости ω3 , т.к. величины ε3 и ω3 одинакового знака. По формулам

(30) и (31) определяем скорость, касательное, нормальное и полное ускорения точки М:

V = ω3 R3 = 10 20 = 200 смс ,

aτ = ε 3 R3 = 20 20 = 400 смс2 , an = ω32 R3 = 102 20 = 2000 смс2 , a = aτ2 + an2 = 400 2 + 2000 2 = 2039,6 смс2 .

Вектор скорости направлен перпендикулярно радиусу ОМ в сторону вращения колеса 3 (рис. 28), нормальное ускорение – по радиусу к центру колеса, а касательное – перпендикулярно радиусу по

направлению углового ускорения ε3 .

44

2.5.3Плоское движение твердого тела

Плоским (плоскопараллельным) движением твёрдого тела называется такое движение, при котором все точки тела движутся в плоскостях, параллельных некоторой неподвижной плоскости.

Изучение плоского движения твёрдого тела сводится к изучению движения плоской фигуры (сечения тела плоскостью, параллельной данной неподвижной плоскости), движущейся в своей плоскости.

Определение скоростей точек твёрдого тела при плоском движении

Скорости двух точек А и В плоской фигуры (твёрдого тела) связаны между собой равенством [1]:

перпендикулярный плоскости движения. Из формулы (3.2) следует, что VBA АВ и VBA = ω АВ . На рисунке 29 показана векторная зависимость (3.1).

Рисунок 29 – Векторная зависимость

45

Формула (32) позволяет определить скорость точки В по известной скорости VA и угловой скорости тела ω.

Проецируя равенство (32) на прямую АВ и ось u,

где VBA = ω АВ.

Решая систему уравнений (34) и (35), определяем β и VB, т.е. направление и модуль скорости точки В:

tgβ = VA sinα + VBA ,

VA cosα

VB = VA cos α . cos β

Если известны модули и направления скоростей точек А и В, то из уравнения (35) можно найти угловую скорость тела, а именно:

ω = VB sin β − VA sinα .

AB

Равенство (34) по сути выражает собой теорему о проекциях скоростей точек твёрдого тела, согласно которой проекции скоростей точек твёрдого тела на прямую, проходящую через эти точки, равны между собой. Многие задачи на определение скоростей точек твёрдого тела при плоском движении могут быть решены при помощи этой теоремы.

Второй метод решения указанных задач основан на использовании понятия мгновенного центра скоростей (МЦС) плоской фигуры. При непоступательном движении плоской фигуры (ω≠ 0) в каждый момент времени существует точка тела, скорость которой равна нулю [1]. Эта точка называется мгновенным центром скоростей и, обычно, обозначается буквой Р. Принимая мгновенный центр скоростей за полюс, из равенства (32) получаем более короткую формулу для определения скоростей точек тела при плоском

46

движении, т.е.:

Из выражения (36) следует, что в каждый момент времени скорость любой точки твёрдого тела при плоском движении равна её скорости в мгновенном вращении тела вокруг мгновенного центра скоростей (рис. 30). Модули скоростей точек А и В тела будут определяться по формулам:

Из выражений (37) следует зависимость:

Выражения (37) ,(38) используются при решении задач.

Способы нахождения мгновенного центра скоростей

1) Известно: VA , ω. МЦС находится на перпендикуляре к VA , проведённом из точки А на расстоянии:

AP = VA .

ω

Направление перпендикуляра соответствует повороту вектора скорости VA на угол 90° в сторону вращения тела (рис. 30).

2) Известно: направления скоростей точек А и В плоской фигуры (рис. 30). МЦС находится в точке пересечения перпендикуляров, восстановленных в точках А и В к скоростям этих точек.

47

3) Известно: скорости двух точек А и В плоской фигуры параллельны между собой, перпендикулярны отрезку АВ, направлены в одну сторону, известны по величине и не одинаковы. МЦС находится в точке пересечения прямой АВ и прямой, проходящей

через концы векторов скоростей VA и VВ (рис. 31).

4) Известно: скорости двух точек А и В плоской фигуры параллельны между собой, перпендикулярны отрезку АВ, направлены в противоположные стороны и известны по величине. МЦС находится аналогично п.3 (рис. 32).

48

5) Известно: скорость двух точек А и В плоской фигуры параллельны между собой и не перпендикулярны отрезку АВ (рис.

33), или скорости VA =VB , и VA ,VB AB (рис. 34). МЦС в данный момент времени не существует или формально находится в бесконечности (АВ = ВР = ∞). В этом случае из формулы (38) следует, что угловая скорость плоской фигуры в данный момент времени равна нулю, т.е. тело совершает мгновенно-поступательное движение, и скорости всех его точек одинаковы.

6) Известно: плоская фигура катится без скольжения по неподвижной кривой (рис. 35). МЦС находится в точке соприкосновения фигуры с кривой.

Задачи, в которых требуется найти скорости различных точек плоской фигуры, а также её угловую скорость в данный момент времени при определённом положении плоской фигуры, решаются методом проекций и (или) при помощи мгновенного центра скоростей.

План решения задач методом проекций

1)Выбрать за полюс точку плоской фигуры, скорость которой известна или легко находится из условия задачи.

2)Найти другую точку плоской фигуры, направление скорости которой также известно или легко определяется.

3)Для этой точки записать векторную формулу скорости вида

49

(3.1) и спроецировать её на прямую, проходящую через полюс и рассматриваемую точку, а также на ось, перпендикулярную этой прямой.

4)Из полученных в п. 3 двух уравнений вида (34) (теорема о проекциях скоростей точек твёрдого тела) и (35) определить скорость рассматриваемой точки и угловую скорость плоской фигуры в данном положении.

5)Зная угловую скорость фигуры и скорость полюса, найти с помощью формулы вида (32) путём проецирования её на оси выбранной системы координат скорости других точек плоской фигуры.

План решения задач при помощи мгновенного центра скоростей

1)Определить положение мгновенного центра скоростей плоской фигуры одним из вышеприведенных способов.

2)Найти расстояние от точки плоской фигуры, скорость которой известна или легко определяется из условия задачи, до мгновенного центра скоростей.

3)По формуле (38) определить угловую скорость плоской

фигуры.

4)Найти искомые величины скоростей точек плоской фигуры, используя формулы (37) или(и) (38). Векторы скоростей точек направлены перпендикулярно отрезкам, соединяющим эти точки с мгновенным центром скоростей в сторону мгновенного вращения тела (угловой скорости).

Пример 1. Плоский механизм состоит из стержней 1, 2, 3, 4 и

ползуна В, соединённых друг с другом и с неподвижными опорами О1, О2 шарнирами; точка D находится в середине стержня АВ (рис. 36). Длины стержней соответственно равны: l1 = 0,4м, l2 = 1,2м, l3 = 1,4м,

l4=1м. Угловая скорость кривошипа О1А равна ω1 = 2 радс . Для

заданного положения механизма определить скорости точек А, В, D, Е и угловые скорости всех его звеньев.

Решение: В данном плоском механизме звенья О1А и О2Е

50

вращаются вокруг соответственно точек О1 и О2 , а звенья АВ и DЕ совершают плоское движение. Решим задачу, рассматривая последовательно движение каждого звена механизма, начиная с кривошипа О1А, угловая скорость которого известна. Определяем скорость точки А во вращательном движении звена O1A:

VA = ω1l1 = 2 0,4 = 0,8 мс .

Вектор скорости VA направлен перпендикулярно стержню О1А в сторону его угловой скорости (рис. 36).

Рисунок 36 – К примеру 1

Рассмотрим плоское движение звена АВ. Скорость точки А уже

известна. Скорость ползуна VB направлена по направляющей

(рис. 36). По теореме о проекциях скоростей точек твёрдого тела для точек В и А рассматриваемого звена можно записать:

VB cos 30° =VA cos 30° .

Отсюда находим скорость точки В:

51

VB =VA = 0,8 мс .

Далее по направлениям скоростей VA и VB находим положение

мгновенного центра скоростей звена АВ. Это будет точка Р2 пересечения перпендикуляров, восстановленных в точках А и В к

векторам VA и VB . В соответствии с направлением скорости VA на

рисунке 36 показываем направление мгновенной угловой скорости ω2 звена АВ и определяем её величину по формуле (38):

перпендикулярно отрезку Р2D в сторону угловой скорости ω2 (рис. 36);

модуль скорости VD вычисляется по формуле (37), т.е.:

VD = ω2 Р2 D = 0,67 1,04 = 0,69 мс , где Р2 D = АР2 cos 30° =1,2 0,867 =1,04 м.

Величину скорости VD также можно определить по формуле

(38):

скоростей для точек Е и D звена DЕ:

м

VE =VD cos 60° = 0,69 0,5 = 0,345 с .

По направлениям скоростей VD и VЕ определяем положение мгновенного центра скоростей Р3 рассматриваемого звена DЕ (рис. 36) и находим угловую скорость ω3 этого звена:

Определение ускорений точек твёрдого тела при плоском движении

Ускорения двух любых точек А и В плоской фигуры (твёрдого тела) связаны между собой зависимостью [1]:

где a A – ускорение точки А (полюса);

aBAn , aBAτ – нормальное и касательное ускорения точки В при

вращении фигуры вокруг полюса А.

При этом:

где ω – угловая скорость тела,

ε– вектор углового ускорения тела, направленный перпендикулярно плоскости движения.

Вектор aBAn всегда направлен от точки В к полюсу А,

aBAτ – перпендикулярно отрезку АВ в сторону углового ускорения тела.

На рисунке 37 показана векторная зависимость (39), где введено обозначение aBА = aBAn + aBAτ – полное ускорение точки В при вращении фигуры вокруг полюса А.

Рисунок 37 – Векторная зависимость

Таким образом, для определения ускорения произвольной точки В необходимо знать ускорение какой-либо другой точки А плоской фигуры, принимаемой за полюс, а также мгновенные угловую скорость ω и угловое ускорение ε фигуры. Тогда, складывая три

вектора aA , aBAn , aBAτ (рис. 37), находим искомое ускорение точки В

как сумму этих векторов.

Такой способ применим в случае, если угол поворота тела задан в виде функции о времени ϕ =ϕ(t) , так как тогда можно определить

мгновенная угловая скорость ω может быть найдена только для данного положения тела. В этом случае мгновенное угловое ускорение

54

ε тела не может быть найдено непосредственно.

Задачи на определение ускорений точек твёрдого тела, тем не менее, могут быть решены, если кроме известного ускорения полюса также будет известна траектория какой-либо другой точки тела (прямолинейная или криволинейная). Проецируя в этом случае равенство (39) на направление отрезка АВ, получаем уравнение с

одним неизвестным aB (если траектория точки В прямолинейна) или

aτB (если траектория точки В криволинейна). При криволинейной

траектории ускорение точки В раскладывается на нормальное и касательное ускорения, т.е.:

одно неизвестное aτBA , после определения которого находится угловое ускорение тела ε в данный момент времени по формуле:

ε = aτBA .

AB

В дальнейшем определение ускорений других точек тела также выполняется по формуле вида (39).

План решения задач

Тип I. Заданы скорость и ускорение одной точки плоской фигуры (или они легко находятся из условия задачи) и траектория другой точки фигуры. Требуется определить ускорения каких-либо точек фигуры.

1) Найти мгновенный центр скоростей тела и по заданной скорости точки тела и расстоянию от неё до МЦС по формуле (3.7) определить мгновенную угловую скорость ω плоской фигуры. Если фигура совершает в данном положении мгновенно-поступательное движение, то ω = 0.

2) Определить скорость точки тела (пусть точка В), заданная

55

траектория которой криволинейна.

3) Найти нормальное ускорение точки В по формуле:

aBn = VB2 ,

ρ

где ρ – радиус кривизны траектории точки В.

При этом вектор aBn направлен по нормали к траектории к

центру кривизны.

4) Выбрать за полюс точку тела (например, точку А), ускорение которой известно или легко находится из условия задачи, и записать векторное выражение (39) для ускорения точки В, т.е.:

Вслучае криволинейных траекторий точек А и В, выражение

(42)принимает вид:

точки В к точке А.

6)Спроецировать выражение (42) или (43) на направление отрезка АВ и из полученного уравнения найти ускорение aB или aτB .

7)Спроецировать уравнение (42) или (43) на ось,

перпендикулярную АВ (при этом величины ускорений aB и aBτ уже будут известны) и из полученного уравнения определить ускорение

aτBА .

8) Найти мгновенное угловое ускорение тела по формуле:

56

Направление углового ускорения определяется направлением вектора ускорения aBτ А

9) Определить при помощи формулы вида (42) ускорение любой точки плоской фигуры.

Тип II. Заданы ускорения двух точек плоской фигуры. Требуется определить мгновенные угловые скорость и ускорение тела, а также ускорение любой его точки.

Пример 3. Для плоского механизма, рассмотренного в примере 1, определить ускорения точек А, В и D, а также мгновенное угловое ускорение звена АВ, если угловое ускорение звена О1А равно

ε1 = 3 радс2 (рис. 38).

Решение. Данная задача определения ускорений точек А, В и D стержня АВ, совершающего плоское движение, относится к задачам типа I, так как скорость и ускорение точки А, как точки вращающегося звена О1А, легко находятся, а траектория точки В задана (прямолинейная направляющая ползуна).

1) Мгновенный центр скоростей и мгновенная угловая скорость звена АВ найдены в решении примера 1, т.е.:

рад

ω2 = 0,67 с .

57

Рисунок 38 – К примеру 3

2) Определяем ускорение точки А, как точки звена О1А,

3) Принимаем за полюс точку А и записываем векторное выражение для ускорения точки В:

где aВ – направлено по направляющей ползуна предположительно вправо;

58

aBAn , aBAτ – нормальное и касательное ускорения точки В вокруг полюса А (рис. 38).

4) Определяем нормальное ускорение точки В вокруг полюса А:

Угловое ускорение ε 2 направленно соответственно ускорению

aВτ A , т.е. по часовой стрелке (рис. 38).

8) Определяем ускорение точки D в соответствии с формулой:

59

перпендикулярно АD в соответствии с направлением углового ускорения ε2 (рис. 38).

Спроецируем выражение (46) на оси x и y (рис. 38), т.е. найдём проекции ускорения точки D на эти оси:

aDx = −aAn cos60° −aτA cos30° −aDAn = −1,6 0,5−1,2 0,87−0,27= −2,11см2

aDy = −aAn cos30° + aτA cos60° − aτDA = −1,6 0,87+1,2 0,5− 0,29= −1,08см2

Вычисляем модуль ускорения точки D: