Исходные данные:
Таблица 1
|
Фал F(a,b,c,d) |
(3,9,11,12,13) |
|
Серия микросхем |
К561 |
|
Требование по выходу |
открытый коллектор с повышенной нагрузочной способностью |
Задание
Разработать принципиальную схему комбинационного логического устройства с четырьмя входами a, b, c и d, обеспечивающего на выходе заданную полностью определенную функцию F(a,b,c,d) алгебры логики (ФАЛ) согласно таблице 1.
Рассмотреть два варианта реализации на базе серии микросхем:
1) реализация на логических элементах 2И-НЕ;
2) реализация на мультиплексорах.
В обоих случаях количество корпусов микросхем должно быть минимальным.
Сравнить полученные схемы по току потребления и времени задержки распространения сигнала.
Решение
Минимизация фал
Пусть ФАЛ КЛУ задана в виде последовательности десятичных чисел:
(1)
Таким образом, для ФАЛ (1) получаем следующую таблицу истинности
|
№ кодовой комбинации |
a |
b |
c |
d |
ВЫХОД |
|
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
1 |
0 |
|
2 |
0 |
0 |
1 |
0 |
0 |
|
3 |
0 |
0 |
1 |
1 |
1 |
|
4 |
0 |
1 |
0 |
0 |
0 |
|
5 |
0 |
1 |
0 |
1 |
0 |
|
6 |
0 |
1 |
1 |
0 |
0 |
|
7 |
0 |
1 |
1 |
1 |
0 |
|
8 |
1 |
0 |
0 |
0 |
0 |
|
9 |
1 |
0 |
0 |
1 |
1 |
|
10 |
1 |
0 |
1 |
0 |
0 |
|
11 |
1 |
0 |
1 |
1 |
1 |
|
12 |
1 |
1 |
0 |
0 |
1 |
|
13 |
1 |
1 |
0 |
1 |
1 |
|
14 |
1 |
1 |
1 |
0 |
0 |
|
15 |
1 |
1 |
1 |
1 |
0 |
Получим алгебраическое выражение ФАЛ в совершенной дизъюнк-тивной нормальной форме (СДНФ) на основе таблицы истинности. Для этого нужно записать ФАЛ в виде суммы логических произведений входных переменных, соответствующих тем кодовым комбинациям, при которых ФАЛ равна единице. Логические переменные входят в эти произведения с инверсией или без нее в зависимости от того, чему равна конкретная переменная, нулю или единице. В рассматриваемом случае по таблице получим
(2)
Черта сверху обозначает инверсию значения переменной (логическое отрицание).
Итак, выражения (1), (2) и таблица истинности описывают в разных формах одну и ту же ФАЛ. Выражение (1) наиболее компактно, однако оно не является алгебраическим. Выражение (2) соответствует алгебре логики, но имеет громоздкий вид (особенно при большом количестве входных переменных) и
требует логических вычислений при необходимости определения конкретных значений ФАЛ. Таблица истинности непосредственно задает эти значения, но форма записи наиболее громоздкая.
Для синтеза КЛУ может использоваться любая форма записи, но предварительно необходимо минимизировать ФАЛ, чтобы КЛУ получилось наиболее простым. Можно преобразовать (2) с помощью теорем алгебры логики, но этот подход чреват ошибками.
На практике обычно применяется так называемая диаграмма Вейча (или карта Карно), представляющая собой своеобразную форму таблицы истинности. Один из вариантов диаграммы Вейча для рассматриваемой ФАЛ показан на рисунке 1
-
cd
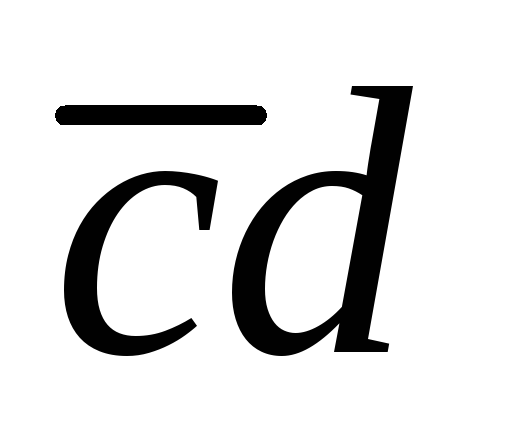
0
0
1
1
1
0
0
0
1
0
0
0
0
1
0
0
Рисунок 1 – Диаграмма Вейчера
Это прямоугольная таблица, в которой число клеток равно количеству возможных кодовых комбинаций.
Таким образом, окончательно минимизированная ФАЛ имеет вид:
(3)
Полученное выражение является основой для синтеза схемы заданного устройства. Для реализации на логических элементах 2И-НЕ‚ как это требуется по условию задачи, выражение (З) может быть преобразовано с помощью процедур двойного отрицания и применения правила Де-Моргана.