
153544-317914
.pdfУДК 528.4(072) ББК 26.14
Ч48
Р е ц е н з е н т ы :
Головань Г.Е, кандидат технических наук (Учреждение образования «Полоцкий государственный университет»);
Зеленский А.М., кандидат технических наук (Учреждение образования «Брестский государственный технический университет»);
Парадня П.Ф., старший преподаватель (Учреждение образования «Полоцкий государственный университет»);
Рекомендовано Советом факультета строительства и транспорта ГрГУ им. Я. Купалы.
|
Черкас, Л.А. |
Ч48 |
Инженерная геодезия : лаб. практикум Л.А. Черкас, Л.Ф. Зуева. – |
Гродно : ГрГУ, 2011. – 145 с. |
|
|
ISBN 978-985-515-400-7 |
|
Изложены теоретические основы выполняемых на занятиях лабораторных работ, |
|
приведены примеры решения задач, вызывающих наибольшие затруднения. Каждой |
|
лабораторной работе предшествует краткое изложение теоретического материала. Рас- |
|
смотрены основные темы: топографические карты и планы, угловые и линейные изме- |
|
рения, нивелирование, геодезические работы при проектировании и перенесении про- |
|
ектов в натуру. Особое внимание уделено устройству и работе с геодезическими прибо- |
|
рами. Адресуется студентам специальностей: «Промышленное и гражданское строи- |
|
тельство», «Производство строительных изделий и конструкций». |
|
УДК 528.4(072) |
|
ББК 26.14 |
|
© Черкас Л.А., Зуева Л.Ф., 2011 |
|
© Учреждение образования |
ISBN 978-985-515-400-7 |
«Гродненский государственный университет |
имени Янки Купалы», 2011 |
ВВЕДЕНИЕ
Практикум по дисциплине «Инженерная геодезия» предназначен для оказания помо-
щи студентам строительных специальностей высших учебных заведений при выполнении лабораторных работ и учебной геодезической практики.
Впрактикуме дается описание топографических карт, методов производства угловых
илинейных измерений на местности, определения площадей. Особое внимание уделено во-
просам устройства, поверок и использования геодезических приборов, организации и вы-
полнению полевых и камеральных работ, а также решению инженерных задач. В практикум включены задания по инженерно-геодезическому проектированию. Некоторые темы, по ко-
торым выполняются расчетно-графические работы, в данном практикуме не освещаются.
В зависимости от объема учебного времени, отведенного на проведение лаборатор-
ных работ, продолжительности и вида обучения (дневное, заочное полное, заочное сокра-
щенное) отдельные задания в соответствии с рабочей программой курса могут выполняться в полном объеме или частично.
Материал практикума изложен по темам программы и состоит из соответствующих заданий. Каждое задание содержит формулировку задачи, цели работы и последовательность выполнения задания. Перед описанием заданий для удобства использования приведены в конспективном виде сведения, необходимые для выполнения работы, для некоторых задач,
вызывающих наибольшие затруднения, приведены примеры решений.
Данный практикум служит дополнением к основной учебной литературе и позволяет студентам приобрести навыки самостоятельного выполнения работ на основе сведений, по-
лученных на лекциях и при самостоятельном изучении учебных изданий.
Все лабораторные работы студентам предлагается выполнять в специальной тетради для лабораторных и самостоятельных работ.
3
РЕКОМЕНДАЦИИ ПО ПОДГОТОВКЕ И ВЫПОЛНЕНИЮ ЛАБОРАТОРНЫХ РАБОТ
Лабораторные работы предназначены для закрепления теоретических знаний, полу-
ченных на лекциях, приобретения навыков в обращении с геодезическими приборами и в об-
работке геодезической документации.
К каждому лабораторному занятию необходимо готовиться. Подготовку начинают с изучения соответствующего раздела в учебнике или по конспекту лекций. Затем необходимо ознакомиться с вводной частью каждого задания в практикуме, где кратко излагается его практическая сущность.
В самом начале первого семестра необходимо самостоятельно изучить правила дейст-
вий с приближенными числами, правила выполнения вычислений, правила составления и ведения технической документации.
ПРАВИЛА СОСТАВЛЕНИЯ И ВЕДЕНИЯ ТЕХНИЧЕСКОЙ ДОКУМЕНТАЦИИ
При полевых и камеральных вычислениях и графических работах серьезное внимание обращают на аккуратность, чистоту и четкость вычерчивания и записей.
Все камеральные вычисления оформляют, как правило, цветом (шариковой и др. ручками).
Каждое записанное число должно содержать такое количество цифр, которое характе-
ризует точность произведенных измерений. Например, если угол измерен до минуты, то пишут 25° 00', а не 25°, если линия измерена с точностью до 0,1 метра, то пишут 314,4 м, а
не 314,40 м, а если до 0,01 м, то 314,40, а не 314,4.
Выполняя действия с числами, нужно цифры подписывать одну под другой. Много-
значные цифры пишут группами по две-три цифры в группе. Например, 6 955 348,4. Целые числа от дробных отделяют запятыми, характеристики от мантисс – точками.
При записях результатов измерений или при действиях с числами часто прибегают к целесообразному округлению чисел.
Правила округления:
1. Если округляемая цифра меньше 0,5 единицы последнего знака, то ее отбрасывают.
Например, число 12,34 с точностью до 0,1 следует записать 12,3.
2. Если округляемая цифра больше 0,5 единицы последнего знака, то число увеличи-
вается на единицу. Например, число 12,36 с точностью до 0,1 следует записать 12,4.
4
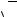
3. Если в числе округляемая цифра 5, то её округляют до четной цифры. Например,
число 12,36 с точностью до 0,1 следует записать 12,4, а если округляемое число 12,45, то его следует также записать 12,4.
Правила действий с приближенными числами. При геодезических измерениях и вычислениях преимущественно имеют дело с приближенными числами. Для правильного действия с числами следует в них различать: десятичные знаки, значащие цифры и верные цифры. Десятичными знаками называются все цифры после запятой. Значащими цифрами называются все цифры числа кроме нулей слева и нулей справа, если последние при округ-
лении подставлены вместо других цифр. Например, число 4108,207 имеет три десятичных знака и семь значащих цифр. Число 0,0035 имеет четыре десятичных знака и две значащие
цифры. Но в числе 3 5 1,7100 пять значащих цифр потому, что в нем нулями не заменены какие-либо цифры. Верными значащими цифрами числа, называются цифры, заслуживаю-
5 1,7100 пять значащих цифр потому, что в нем нулями не заменены какие-либо цифры. Верными значащими цифрами числа, называются цифры, заслуживаю-
щие доверия. Например, если результаты измерения записаны так: 125,33 м, а измерения производились до одного метра, то в этом числе будет лишь три (125) верные цифры, а по-
следние неверные, не заслуживающие доверия.
При вычислениях удерживают такое количество значащих цифр, десятичных знаков,
которое обеспечивает нужную точность результатов и не загружает вычисления неверными,
или ненужными цифрами.
При вычислениях необходимо соблюдать следующие правила:
-если числа содержат неодинаковое количество десятичных знаков, то при их сло-
жении и вычитании оставляют столько десятичных знаков, сколько их имеет приближенное число с наименьшим количеством десятичных знаков, плюс один запасной;
- если приближенные числа содержат неодинаковое количество значащих цифр, то при умножении или делении в результате оставляют столько значащих цифр, сколько их имеется в приближенном числе с наименьшим количеством значащих цифр, плюс одна за-
пасная цифра;
-при возведении числа в степень в полученном числе надо оставить столько зна-
чащих цифр, сколько их было в числе, возводимом в степень;
-в подкоренном выражении надо оставлять такое количество значащих цифр, ка-
кое хотим получить в результате извлечения корня.
5

ЕДИНИЦЫ МЕР, ПРИМЕНЯЕМЫЕ В ГЕОДЕЗИИ
В геодезии измеряются различные величины. Под величиной понимают количествен-
ную характеристику физического тела, процесса или явления. Измерить величину – значит определить ее числовое значение в принятых единицах измерения.
При производстве геодезических измерений применяются меры длины, площади, ве-
са, температуры, давления, угловые меры и другие.
Единицей измерения угла (горизонтального и вертикального) являются:
– градус, получающийся делением прямого угла на 90 равных частей. Один градус ра-
вен 60 минут, а одна минута – 60 секунд (1° = 60' = 3 600");
– радиан, представляющий собой центральный угол, опирающийся на дугу, длина которой равна радиусу этой окружности. Значение радиана в градусной мере равно
ρ = 57,3º = 3438' = 206 265". Для перевода значения угла из градусной меры в радианную
нужно разделить его на радиан: ' " ;
' "
– град (в настоящее время называют гон) получающийся делением прямого угла на
100 равных частей или окружности на 400 частей. Один град равен 100 десятичных минут, а
одна десятичная минута – 100 десятичных секунд (1g = 100с = 10 000сс).
За единицу линейных измерений (расстояний, горизонтальных проложений, высот превышений) в геодезии принят метр. 1 метр равен расстоянию, которое свет проходит в вакууме за 1/299 792 458 доли секунды; 1 километр; 1 км = 1000 м; 1 дециметр; 1 дм = 0,1 м; 1 сантиметр; 1 см = 0,01 м; 1 мм = 0,001 м.
Для измерения площадей:
–километр квадратный; 1 км2 = 1 000 000 м2 = 100 га;
–гектар; 1 га = 10 000 м2;
–1 дм2 = 0,01 м2;
–1 см2 = 0,0001 м2.
6
ТЕМА: «ТОПОГРАФИЧЕСКИЕ ПЛАНЫ И КАРТЫ»
ЛАБОРАТОРНАЯ РАБОТА № 1
МАСШТАБЫ. РАБОТА С ПОПЕРЕЧНЫМ МАСШТАБОМ
Цель работы: познакомиться с топографическими картами; изучить масштабы, при-
меняемые в геодезии; научиться определять расстояния на топографической карте с помо-
щью поперечного масштаба.
Общие сведения о топографических картах и планах
Поверхность Земли изображают на плоскости в виде карт, планов, профилей. Топо-
графические карта и план являются уменьшенным изображением земной поверхности на плоскости. При составлении карт и планов сферическую поверхность Земли проецируют на горизонтальную плоскость, и полученное изображение уменьшают до требуемого размера.
Для составления топографических планов применяют метод ортогонального проеци-
рования. Его сущность: все точки местности переносят на горизонтальную плоскость по от-
весным линиям, параллельным друг другу и перпендикулярным горизонтальной плоскости.
Таким образом, планом называют уменьшенное подобное изображение небольшого участка местности на плоскости (на бумаге), без учета кривизны земной поверхности.
Топографические планы создаются в масштабах 1:5 000, 1:2 000; 1:1 000 и 1:500. Они предназначаются для разработки генеральных планов, технических проектов и рабочих черте-
жей при обеспечении строительства различных инженерных сооружений.
Карта – это уменьшенное, измеримое и обобщенное изображение на плоскости участков поверхности Земли или небесных тел, построенное по определенным математическим законам наглядно показывающее при помощи условных знаков размещение и связи различных предме-
тов и явлений, а также их качественные и количественные характеристики.
По предмету изображения карты подразделяются на астрономические и географиче-
ские. В свою очередь, географические карты подразделяются по содержанию на общегео-
графические и тематические, а по назначению – на карты универсальные (многоцелевые) и
специальные.
Общегеографические карты универсального назначения изображают земную поверх-
ность с обязательным совместным показом всех ее элементов: населенных пунктов, гидрогра-
фии, дорожной сети, растительного покрова и т.д., с подробностью определенной масштабом
7
карты. Среди общегеографических карт наибольшее значение и распространение имеют то-
пографические карты, составленные в масштабах 1:10 000 – 1:1 000 000.
Топографические карты подразделяют на:
-крупномасштабные – 1:10 000; 1:25 000; 1:50 000;
-среднемасштабные – 1:100 000; 1:200 000; 1:300 000;
-мелкомасштабные – 1:500 000 и 1:1 000 000.
Топографические карты в масштабах до 1:500 000 включительно принято составлять в равноугольной проекции Гаусса, а карты масштаба 1:1 000 000 – в видоизмененной полико-
нической проекции.
В основном, топографические карты создают путем аэрофотосъемки или космической съемки. Для небольших территорий применяют наземные методы топографических съемок.
К специальным картам относят авиационные, гравиметрические и морские; к темати-
ческим – дорожные, рельефные, геологические, почвенные, геоботанические, экономиче-
ские, синоптические и др.
Понятие о цифровых топографических картах. Лист обычной топографической карты – это результат работы сложного научно-производственного конвейера, в котором ре-
ализованы достижения науки и техники нескольких поколений ученых и специалистов раз-
ного профиля. К этим достижениям относятся:
математическая основа, включающая больше десятка картографических проекций;
система разграфки и номенклатуры;
наборы условных знаков для всего масштабного ряда карт;
высокопроизводительные способы съемки местности;
технология создания оригиналов на жесткой недеформируемой основе;
способы тиражирования цветных оттисков карт самого разного назначения.
Всеобщая информатизация и компьютеризация проявляются кроме всего прочего в создании цифровых моделей самых разных объектов и явлений. В этом смысле топографиче-
ские карты, являясь графической моделью земной поверхности, уже не удовлетворяют со-
временным требованиям, и основным продуктом топографии становятся цифровые топогра-
фические карты.
Цифровая топографическая карта – это набор метрической (числовой), семантической
(описательной) и логической информации об участке земной поверхности, хранящийся в за-
кодированном виде на каком-либо носителе, доступном для компьютера. Компактность хра-
нения информации, оперативность ее обновления и широкий набор возможностей примене-
ния ее для решения различных задач – обязательные атрибуты цифровых карт. Существую- 8
щие технические и программные средства позволяют просматривать и редактировать цифро-
вую карту на экране дисплея, выполнять различные расчеты, готовить и выводить на прин-
тер или плоттер необходимые документы.
Цифровая топографическая карта, являясь цифровой моделью местности, должна не только включать в себя прежнюю – графическую модель, но и обладать рядом новых свойств, расширяющих и упрощающих использование геодезической информации.
В настоящее время широко используется понятие ГИС – геоинформационная систе-
ма. В отличие от других автоматизированных информационных систем в геоинформацион-
ных системах используется информация о земной поверхности и об объектах естественного и искусственного происхождения, расположенных на ней и вблизи нее, то есть информаци-
онной основой ГИС являются данные о земной поверхности, представляемые в виде цифро-
вых карт.
Некоторые сферы применения ГИС:
инвентаризация и учет природных ресурсов;
территориальное управление;
ведение различных кадастров (земельного, водного, лесного, городского и др.);
управление крупными топливно-энергетическими комплексами;
управление транспортом;
управление службами безопасности (армия, внутренние войска);
городское управление;
управление недвижимостью и т.д.
Масштабы: численный, линейный, поперечный
Масштабом называется степень уменьшения горизонтального проложения линии местности при изображении ее на карте или плане.
Под южной рамкой карты помещены три вида масштабов: численный, именованный и линейный.
Численный масштаб. Масштаб карты, как правило, выражают в виде простой дроби
1:М. Такой масштаб называют численным. Знаменатель М численного масштаба является от-
влечённым числом, которое показывает, во сколько раз уменьшены горизонтальные проло-
жения при изображении их на карте. Так, на картах масштабов 1:500; 1:10 000 и 1:50 000 го-
ризонтальные проложения уменьшены соответственно в 500; 10 000 и 50 000 раз.
9
Если длину линии на карте обозначить через D, то ей будет соответствовать горизон-
тальное проложение линии местности d.
d D M . |
(1) |
Пример 1. Длина отрезка на карте масштаба 1:50 000 D = 4,2 см. Определить соответ-
ствующее горизонтальное проложение d. Согласно (1) имеем:
d = 4,2 см · 50 000 = 210 000 см = 2 100 м.
Пример 2. Длина горизонтального проложения линии местности d = 897 м. Опреде-
лить ее длину на карте масштаба 1:25 000. Из формулы (1) найдём d
D = d : M = 897 м : 25 000 = 0,035 88 м = 3,59 см.
Чем меньше знаменатель численного масштаба М, тем крупнее масштаб, и, наобо-
рот, чем больше знаменатель М, тем мельче масштаб. Например, масштаб 1:500 крупнее масштаба 1:20 00 в 4 раза, а масштаб 1:5 000 мельче масштаба 1:100 в 5 раз.
При пользовании численным масштабом приходится выполнять вычисления. Это не всегда удобно при большом объеме выполняемых работ. Поэтому иногда удобнее пользо-
ваться графическими построениями численного масштаба, которые называются линейным и поперечным масштабами.
Линейный масштаб удобнее при измерении расстояний по карте. Линейный масштаб помещен под южной рамкой карты. Деления линейного масштаба оцифрованы в метрах в соответствии с численным масштабом карты, для которой он построен. На рисунке 1 пред-
ставлен линейный масштаб для плана масштаба 1:2 000.
Для построения линейного масштаба на прямой АВ, начиная от одного из его концов, от-
кладывают отрезки одинаковой длины, называемые основанием масштаба (а). На рисунке 1 ос-
нование масштаба составляет 2 см. После первого основания ставят 0 и от него влево и вправо делают соответствующую масштабу оцифровку. Для повышения точности измерений слева от нуля основания делят на более мелкие деления. Длину отрезка на карте измеряют циркулем-
измерителем. Не изменяя раствора ножек, измеритель прикладывают к линейному масштабу так, чтобы правая ножка совмещалась с каким-нибудь делением справа от нуля, а левая находи-
лась на левом основании масштаба, и отсчитывают значение расстояния.
Именованный масштаб – это словесное выражение численного масштаба. Например,
для масштаба 1: 10 000 именованный будет: «в 1 сантиметре 100 метров».
10
40 |
0 |
40 |
80 |
120 |
160 |
А |
|
|
|
|
В |
а = 2 см
D
СD = 80 + 22 = 102 метра
С
М1:2 000
в1 сантиметре 20 метров
Рисунок 1 – Определение расстояний при помощи линейного масштаба
Линейный масштаб не всегда позволяет измерить расстояние с необходимой точностью.
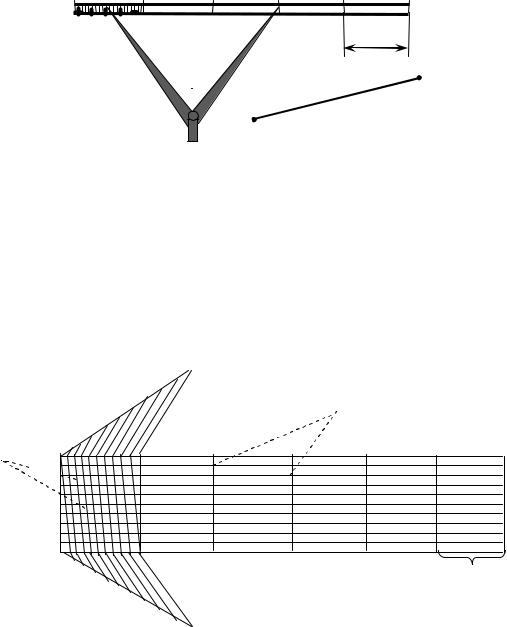
Высокую точность получают при помощи поперечного масштаба. Для его построе-
ния на прямой линии откладывают последовательно несколько раз основание масштаба а
(обычно а = 2 см рисунок 2). Основание масштаба также может быть равным 1, 2, 4 и 5 см.
В
вертикали
С
трансверсали А
m
А'
С'
а
n
В'
Рисунок 2 – Поперечный масштаб
Из полученных точек восстанавливают перпендикуляры, которые называют вертика-
лями. На крайних вертикалях откладывают m равных отрезков (обычно m = 10) и через полу-
ченные точки проводят линии, параллельные основанию – горизонтали. Крайнее левое осно-
вание делят на 10 частей методом параллельных линий. Для этого строят вспомогательные отрезки АВ и А'В' (рисунок 2.2). Вспомогательные отрезки АВ и А'В' проводятся произволь-
ной длины и под произвольным углом к основанию. Эти отрезки делят на 10 равных между
собой частей. Таким образом, нижнее и верхнее основания делят на 10 равных частей (n = 11
