Координаты и параллаксы точек стереопары

Положение соответственных точек на паре снимков определяю в прямоугольных плоских системах координат

Разности абсцисс соответственных точек стереопары называется продольным параллаксом (p).

Разность ординат этих точек называется поперечным параллаксом (q)

Пусть правый снимок стереопары наложен на левый так что системы координат совпали. Тогда продольный параллакс будет представлять собой проекцию расстояний между соответственными точками на ось x, а поперечный на ось y.

Продольный параллакс зависит от рельефа местности, если местность плоская, то «p» = const для все точек стереопары и приблизительно равен базису фотографирования

Поперечный параллакс зависит от углов наклона и разворота снимков, если снимки горизонтальные (трансформированные) в идеальном случае q = 0.

Элементы ориентирования пары снимков

Элементы внешнего ориентирования пары снимков определяют положение левой и правой связок во время фотографирования.

К ним относятся:

α₁ – продольный угол наклона – угол между осью z и проекцией главного луча на

ω₁- поперечный угол наклона левого снимка – угол между главным лучам и плоскостью xz.

ᴂ₁ – угол поворота левого снимка – угол между осью у1 и плоскости проходящей через главный луч и ось Y.

α₂ω₂ᴂ₂ - угловые элементы ориентирования пары снимка

Xs₁Ys₁Zs₁ – координаты левой точки фотографирования во внешней системе координат

Xs₂Ys₂Zs₂ координаты правой точки фотографирования во внешней СК.

Xs₁Ys₁Zs₁, Xs₂Ys₂Zs₂ – линейные элементы ориентирования пары снимков

При аэросъёмке левый и правый снимки стереопары получаются обычно одним и тем же фотоаппаратом. Поэтому можем считать, что элементы внутреннего ориентирования x₀ y₀ f (элементы внутреннего ориентирования) одинаковы.

Таким образом пара снимков имеет 3 элемента внутреннего ориентирования и 12 элементов внешнего ориентирования.

Зависимость между координатами точки объекта и координатами ее изображений на стереопаре

Пусть с коyцов базиса S1 и S2 получена пара снимков p1 и p2. Найдем координаты точки А полагая, что элементы ориентирования снимков известны.

Величина и направление базиса определяется вектором . Причемяв- ся координатамиS₂ в СК

Положение вектора это координаты точки А в СК

Вектора – коллинеарные, поэтому

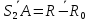и коллинеарные, с другой стороны все эти вектора лежат в одной плоскости следовательно они компланарны, т.е

Формулы (1) и (2) представляют математическую зависимость в векторной форме, что бы представить эту зависимость в координатной форме спроектируем векторы на координатные оси.

А для 2 ого случая:

Формулы 3получены для общего случая

Рассмотрим частный случай съемки, в котором снимки горизонтальные и получены с одной и той же высоты. При этом оси координат х1 и х2 параллельны базису. Принимая левый конец базиса за начало фотограмметрической СК совместим ось Х с базисом, а ось Z с главным лучом левой связки.

Идеальный случай:

Рассмотрим формулу 3 для частного случая

; ;

Решение фотограмметрических задач по горизонтальным снимкам значительно облегчается по сравнению с обработкой наклонных снимков, поэтому на практике часто результаты измерений наклонных снимков приводят горизонтально, т.е делают трансформированным, а затем используют формулы (4)