5

5. Достоинства и недостатки традиционных методов.

Достоинства:

1. Координаты определяются сразу в требуемой системе координат (например государственной СК или МСК), не существует проблемы преобразования из системы координат измерений в локальную СК

2. Нормальные высоты получаются сразу из измерений (геометрическим нивелированием).

3. Возможно применять в любых условиях и любой ситуации на местности: в лесу, в сплошной городской застройке, под землей

3. Точность определения зависит от применяемых приборов и методик: можно всегда выбрать оптимальный по соотношению цена-точность вариант

4. Есть различные варианты стоимостных решений традиционных геодезических приборов от недорогих (оптические инструменты), средних – приборы технической точности, до высокоточных, дорогих оптико-электроннных приборов (тахеометры)

5. Хорошо разработаны методики измерений традиционными методами и обработки полученных измерений

Недостатки:

1. При построении геодезических сетей существует необходимость обеспечивать пря­мую видимости между пунктами. Поэтому нужно строить высокие знаки-сигналы, выбирая места на возвышенностях.

2.Новые пункты закладывают не в местах, удобных для подъезда, а в местах, обеспечивающих прямую видимость между смежными пунктами.

3. Более высокая трудоемкость. Производительность труда традиционных методов определения координат по сравнению со спутниковыми технологиями ниже 10-15 раз.

4. Невозможность кинематических измерений, измерения возможны только между неподвижными объектами

5. Плановые и высотные сети разделены, поэтому одновременно с высокой точностью могут определяться только либо плановые координаты (x,y), либо нормальная высота (из нивелирования). Деление класси­ческих геодезических сетей на плановые и высотные привело к тому, что на пунктах триангуляции оказываются грубые высотные отметки, а на реперах отсутствуют плановые координаты.

6. Более низкий, по сравнению со спутниковыми методами уровень автоматизации, возможны грубые и субъективные ошибки.

7. Высокая зависимость от погоды (при непогоде – дождь, снег, туман, дымка, дым) отсутствует видимость. В отдельные периоды из-за недопустимого влияния внешней среды (солнечная рефракция) измерения также запрещены (особенно высокоточные)

20. Методы, средства и порядок математической обработки спутниковых измерений. Концепции уравнивания спутниковых измерений. Решение базовых линий, контроль качества решений.

Методы и порядок математической обработки спутниковых измерений – обработка ГНСС-измерений и вычисление базовых линий, вычисление невязок замкнутых фигур, оценка точности измерений по невязкам фигур, уравнивание сетей, оценка точности по результатам уравнивания

Средства математической обработки спутниковых измерений – специальное коммерческое ПО для обработки спутниковых измрений

Концепции уравнивания

В общем случае кампания ГНСС измерений включает использование небольшого числа приёмников для определения координат большого количества станций. Выполненные в проекте наблюдения разделяются на сессии, состоящие из наблюдений на отдельных станциях (пунктах). Сессия может быть короткой, всего несколько минут, если в малой сети применяется метод быстрого разрешения неоднозначностей, или несколько часов и даже суток, если необходимо достигать высокую точность в более крупных сетях. При ограниченном числе доступных спутников типичная сессия наблюдения в инженерных сетях продолжается от 1 до 3 часов. Разработаны и используются следующие методики уравнивания спутниковых наблюдений:

• уравнивание наблюдений, выполненных на одной станции;

• обработка одной базовой линии и последующее объединение базовых линий в сеть,

• объединенное уравнивание всех полученных наблюдений отдельной сессии (уравнивание наблюдений многих станций одной сессии), и

• объединение решений многих сессий в строгое всеобщее сетевое решение,

• объединение спутниковых и традиционных геодезических измерений.

Уравнивание одной станции (позиционирование точки, «однопунктовое» решение) обеспечивает абсолютные координаты станции в системе WGS-84 (или ПЗ-90). Если обрабатываются только кодовые измерения, то из-за низкой точности эти результаты обычно представляют малый интерес для геодезических применений, но они часто отвечают требованиям некоторых задач геофизики, ГИС и дистанционного зондирования. Типичная область этого применения – навигация.

Концепция одинарной базовой линии очень широко используется в программном обеспечении для обработки спутниковых данных. В совместном уравнивании обрабатываются наблюдения от двух одновременно работавших приемников, преимущественно в виде двойных разностей. Результатом являются компоненты вектора базовой линии и соответствующая ковариационная матрица K_XYZ.

Отдельные базовые линии используются как исходные данные в программе уравнивания сети. Обработка наблюдений в сети распадается на первичное уравнивание (решение базовых линий) и вторичное уравнивание (уравнивание векторов базовых линий). Эта методика является строгой, если одновременно наблюдали только два приемника, и если используется вся стохастическая информация полной ковариационной матрицы. Однако если пары станций выбраны из большего числа одновременно действовавших приемников, то не все возможные комбинации базовых линий не зависят одна от другой. Для улучшения решения необходимо тщательное взвешивание и ослабление корреляции.

Большинство производителей предлагают вместе с приемниками программы, которые используют концепцию базовых линий. Эти программы удобны для малых проектов, для полевой проверки данных и для применений в реальном времени.

В уравнивании многих станций одной сессии совместно обрабатываются все данные, которые наблюдались одновременно тремя или более участвующими приемниками. В этом случае результатами решения являются R-1 независимых векторов и ковариационная матрица размера 3(R-1) 3(R-1). В зависимости от имеющегося программного обеспечения, результаты можно также выдавать набором из 3R координат и ковариационной матрицы размером 3R3R. Ковариационная матрица также является блочно-диагональной, в которой размер ненулевых диагональных блоков является функцией числа приемников R. Следовательно, это строгое уравнивание наблюдений с использованием всех взаимных стохастических соотношений. Для геодезических целей такое «многопунктовое» уравнивание имеет концептуальные преимущества над методом базовых линий, поскольку используется весь потенциал точности СРНС.

Несколько решений по сессиям можно объединять в уравнивание многих сессий или, более точно, в решение по многим станциям и многим сессиям. Это обычная методика, когда крупные сети разбиваются на части из-за ограниченного числа приемников. Основное условие в таком уравнивании состоит в том, что каждая сессия связывается хотя бы с одной другой сессией через одну или большее количество общих станций, на которых наблюдения выполнялись в обе сессии. Расширение числа общих станций повышает стабильность и надежность всей сети.

Объединение спутниковых и традиционных видов измерений необходимо для перехода от общеземных координат точек спутниковой сети к государственной референцной системе СК-95 и к Балтийской системе нормальных высот.

Решение базовых линий, контроль качества решений – см.Вопрос 19 ответ тот же приводится ниже

Полевые контроли спутниковых измерений.

Контроль отдельных базовых линий осуществляется по тип окончательного решения. Лучшим типом решения для одночастотных измерений являются фиксированное по двойным разностям, для двухчастотных измерений – фиксированное по двойным разностям ионосферно-свободной комбинации фаз. Плавающие решения, как правило, приемлемы для средних базовых линий, в десятки и сотни километров длиной. Погрешности таких решений обычно больше половины длины волны, то есть 10 см.

При расстояниях между пунктами в 20-30 км средние квадратические ошибки длины вектора базовой линии и его компонент в общеземной или локальной геодезической системах обычно находятся в пределах 1 – 2 мм. К средней квадратической ошибке одного измерения очень близка ошибка rms. Полезную информацию о погрешностях дает апостериорная ковариационная матрица (кофакторная матрица). Однако эти данные характеризуют точность лишь по внутренней сходимости.

В связи с тем, что для системы уравнений поправок находится несколько наборов целочисленных неоднозначностей, выбор лучшего из них производится на основании F-теста или Ratio. В этом исследовании соответствующие каждому набору дисперсии располагаются в порядке возрастания и берется отношение дисперсии второго претендента на решение к дисперсии первого претендента на решение 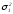то есть к наименьшей из всех дисперсий:

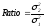. (10.30)

Полагая, что лучшему решению соответствует минимальная дисперсия, обычно при Ratio > 1.5 с вероятностью 95 % ПБЛ присваивает ему тип фиксированного решения. Если Ratio1.5, то первому претенденту на решение присваивается тип плавающего решения.

Тест на относительную дисперсию Reference Variance (RV) проверяет соответствие апостериорной и априорной дисперсий:

(10.31)

Относительная дисперсия является индикатором того, насколько хорошо наблюдалась базовая линия. Эта величина не имеет размерности, иногда ее называют коэффициентом дисперсии или дисперсией единицы веса. Она показывает, насколько полученные данные соответствуют тому, что ожидалось получить. Априорная дисперсия рассчитывается на основе предсказания о нормальном уровне ошибок в измерениях (уровне шумов). Если предположения о суммарном влиянии ошибок оправдалось, то RV=1. При RV<1 можно утверждать, что данные получены более качественные, чем ожидалось, при RV>1 - ожидания не оправдались. Для одночастотных статических измерений нормальное значение относительной дисперсии может быть около 4, а для кинематических съемок, когда положение выводится из 1 – 2 эпох, Reference Variance может быть порядка 5 – 6 и более.

Высокое Reference Variance и низкое Ratio могут быть следствием ряда причин:

• шумные данные, вызванные частичными препятствиями, например, деревьями, данными от спутников вблизи горизонта,

• значительная многопутность,

• немоделируемые систематические ошибки, особенно при одночастотных измерениях на линиях длиннее 15-20 км, где могут быть проблемы с учетом ионосферной рефракции,

• неправильный выбор фиксированного решения.

Линия в 30 км, измеренная одночастотными приемниками, может иметь относительную дисперсию от 10 до 20 из-за влияния ионосферы. Линия в 1 км, измеренная в режиме быстрой статике в 5-минутном сеансе, может иметь высокую относительную дисперсию из-за многопутности. Наблюдения двухчастотной аппаратурой небольших базовых линий (до 10 км) дают относительную дисперсию 0.8-1.0, если на обоих концах линии отсутствуют препятствия. Если на одном конце находится 4-х метровая пирамида из металлического уголка, относительная дисперсия возрастает до 2 – 4 , если пирамиды на обоих концах, - то до 6 – 8. Несмотря на то, что сигналы не имеют потерь в счете циклов, возникающая из-за стоек пирамиды многопутность ухудшает качество измерений [Антонович, 1997].

Важную информацию для анализа решения могут дать графики остаточных невязок уравнений наблюдений.

Ошибки элементов приведения, ошибки фазового центра не сказываются на качественных характеристиках решения базовой линии, они выявляются при вычислении невязок в замкнутых фигурах.

Контроль сетей Для сетей наилучшим средством нахождения проблемных линий является использование программ замыкания фигур, которые для определения невязок суммируют компоненты векторов по замкнутому контуру. Большинство программных пакетов имеют именно этот тип программ. В каждой фигуре можно получить невязки w_X, w_Y, w_Z или w_E, w_N, w_U по каждой из координат как сумму соответствующих приращений, которая теоретически должна равняться нулю:

, (10.32)

где k – число сторон в замкнутой фигуре.

По координатным невязкам можно получить полную невязку w:

(10.33)

и сравнить ее с допустимой (ожидаемой) невязкой w_доп.:

(10.34)

Ошибки _D, _H определяются на основании паспортных данных или устанавливаются на основании инструкций для данного вида работ. С вероятностью 95% должно выполняться условие:

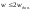. (10.35)

Преимущество контроля по невязкам очевидно: здесь осуществляется не только контроль решения базовой линии, но и ошибки оператора. Большие невязки w_E, w_N свидетельствуют о грубом центрировании антенны, а большая невязка w_H –о промахе при измерении высоты. Недостаток метода контроля по невязкам состоит в невозможности контролировать смещенные решения базовых линий. Один из источников таких решений – ошибки в априорных координатах начала базовой линии.

В статье [Герасимов, Сластенов, 1994] дается формула средней квадратической ошибки измерения одной разности координат по невязкам фигур всей сети:

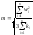. (10.36)

В этой формуле в числителе должна быть сумма квадратов полных невязок из n замкнутых фигур, а в знаменателе – сумма числа сторон во всех фигурах, k – число сторон в фигуре. Если требуется сделать оценку точности по каждой из координат в отдельности, то формулу нужно изменить: в числителе вместо полных невязок использовать только невязки по соответствующей координате, а в знаменателе необходимо убрать коэффициент 3. При этом важно, чтобы одна и та же базовая линия присутствовала только в одной

21. Государственная нивелирная сеть. Назначение и требуемая точность. Схема и программа построения нивелирной сети на разных этапах ее развития. Методы высокоточного нивелирования, гравиметрическое обеспечение нивелирных линий.

Государственная нивелирная сеть. Назначение и требуемая точность. Схема и программа построения нивелирной сети на разных этапах ее развития.см. вопрос 4

Методы высокоточного нивелирования, гравиметрическое обеспечение нивелирных линий.

Геометрическое Нивелирование выполняют путём визирования горизонтальным лучом трубой нивелира и отсчитывания высоты визирного луча над земной поверхностью в некоторой её точке по отвесно поставленной в этой точке рейке с нанесёнными на ней делениями или штрихами). Обычно применяют метод Нивелирование из середины, устанавливая рейки на башмаках или колышках в двух точках, а нивелир - на штативе между ними (рис. 1).

  В зависимости от точности и последовательности выполнения работы по геометрическому Нивелирование подразделяются на классы. Государственная нивелирная сеть СССР строится по особой программе и делится на 4 класса. Нивелирование I класса выполняют высокоточными нивелирами и штриховыми инварными рейками по особо выбранным линиям вдоль железных и шоссейных дорог, берегов морей и рек, а также по др. трассам, важным в том или ином отношении. По линиям Нивелирование I класса средняя квадратичная случайная ошибка определения высот не превышает ±0,5 мм, а систематическая ошибка всегда менее ±0,1 мм на 1 км хода. В СССР Нивелирование I класса повторяют не реже, чем через 25 лет, а в отдельных районах значительно чаще, чтобы получить данные о возможных вертикальных движениях земной коры. Между пунктами Нивелирование I класса прокладывают линии Нивелирование II класса, которые образуют полигоны с периметром 500-600 км и характеризуются средней квадратичной случайной ошибкой около ±1 мм и систематической ошибкой ±0,2 мм на 1 км хода. Нивелирные линии III и IV классов прокладываются на основе линий высших классов и служат для дальнейшего сгущения пунктов нивелирной сети. Для долговременной сохранности нивелирные пункты, выбираемые через каждые 5-7 км, закрепляются на местности реперами или марками нивелирными, закладываемыми в грунт, стены каменных зданий, устои мостов и т.д.