
Учебные материалы по разделам курса физики
1 Механика
Основные формулы и определения
● Согласно
второму закону Ньютона, произведение
массы тела на его ускорение равно
результирующей силе, действующей на
тело: ![]() = m·
= m·![]() .
.
В
другой форме второй закон Ньютона имеет
вид: ![]() =
d
=
d![]() /dt,
где
/dt,
где
![]() -
импульс
тела,
d
-
импульс
тела,
d![]() /dt
– производная от импульса по времени.
/dt
– производная от импульса по времени.
Для движения вдоль оси x второй закон Ньютона имеет вид: Fx =dpx /dt , где Fx -проекция силы на ось , dpx /dt – производная от компоненты импульса по времени.
● Полное
ускорение равно векторной сумме
нормального и тангенциального ускорения:
![]() =
=
![]() n
+
n
+
![]() τ
.
τ
.
Нормальное ускорение a n характеризует изменение скорости по направлению, направлено перпендикулярно скорости и равно:
a n = v 2/R, где v – скорость точки, R – радиус кривизны траектории .
Тангенциальное ускорение а τ характеризует изменение скорости по величине (или по модулю), направлено параллельно скорости и равно производной от скорости по времени: а τ=dv/dt .
● Импульсом
тела называется произведение массы
тела на его скорость:
![]() =
m
=
m![]() .
Импульсом
системы тел называется сумма импульсов
всех тел, входящих в систему. Импульс
замкнутой системы тел сохраняется.
.
Импульсом
системы тел называется сумма импульсов
всех тел, входящих в систему. Импульс
замкнутой системы тел сохраняется.
● Кинетическая энергия поступательного движения тела равна Wk= mv 2/2.
Потенциальная энергия тела, поднятого на высоту h, равна Wp = m g h ,
где g = 9,8 м/с2 – ускорение свободного падения, причём, высота h много меньше радиуса Земли RЗемли .
Потенциальная энергия упруго деформированной пружины равна: W p= k x2/2, где k – коэффициент упругости, x – деформация (изменение длины пружины).
● Полная механическая энергия тела равна сумме кинетической и потенциальной энергий: W ПОЛН. =Wk + Wp .
Закон сохранения энергии формулируется так: полная механическая энергия замкнутой системы, между телами которой действуют только консервативные силы (например, сила тяжести, сила упругости), сохраняется.
● Если
потенциальная энергия зависит только
от одной координаты, то проекция силы
на ось х равна производной от потенциальной
энергии по этой координате, взятой с
обратным знаком: Fx
=
-
![]() .
.
● Угловой скоростью называется производная от угла поворота по времени: ω = dφ /dt.
Угловым ускорением называется производная от угловой скорости по времени: ε = dω /dt.
● Моментом инерции материальной точки называется произведение массы материальной точки на квадрат её расстояния до оси вращения: I = m r 2.
● Моментом
инерции твёрдого тела называется
сумма произведений масс материальных
точек на квадраты их расстояний до
оси вращения:
I
= ![]() i
2.
Момент инерции тела относительно оси
симметрии, проходящей через центр масс
тела, равен:
i
2.
Момент инерции тела относительно оси
симметрии, проходящей через центр масс
тела, равен:
1) для обруча (полого цилиндра) I0 = m R 2,
2) сплошного цилиндра (диска) I0 = m R 2 / 2,
3) шара I0 =(2/5)·m R 2 ,
4) стержня, I0 = (1/12) ml2, где l – длина стержня.
Согласно теореме Штейнера, момент инерции тела относительно произвольной оси равен моменту инерции этого тела относительно оси, параллельной данной и проходящей через центр масс, плюс произведение массы тела на квадрат расстояния между осями: I = I0 + m·d2.
● Момент
силы равен векторному произведению
радиуса – вектора на силу: ![]() = [
= [![]() ·
·
![]() ],
где
],
где ![]() –
радиус – вектор, проведенный от оси
вращения в точку приложения силы. Модуль
момента силы равен:
–
радиус – вектор, проведенный от оси
вращения в точку приложения силы. Модуль
момента силы равен:
M
= F·r·sin(α),
где α – угол между силой ![]() и радиусом – вектором
и радиусом – вектором ![]() .
.
● Момент
импульса материальной точки равен
векторному произведению радиуса –
вектора на импульс: ![]() =
[
=
[![]() ·
·
![]() ],
где
],
где ![]() –
радиус – вектор, проведенный от оси
вращения в точку приложения импульса.
Модуль момента импульса материальной
точки равен L
= m∙v∙r·sin
α, где α – угол между вектором импульса
m
–
радиус – вектор, проведенный от оси
вращения в точку приложения импульса.
Модуль момента импульса материальной
точки равен L
= m∙v∙r·sin
α, где α – угол между вектором импульса
m![]() и
радиусом – вектором
и
радиусом – вектором ![]() .
.
Модуль момента импульса твердого тела численно равен произведению момента инерции тела на его угловую скорость: L= I·ω.
● Согласно основному закону динамики вращательного движения, результирующий момент сил, действующих на тело, равен производной от момента импульса по времени: M = dL / dt. В другой форме: M = I∙ε (при I=const).
Тест 1 - 1
Если
а![]() и
аn-тангенциальное
и нормальное ускорение, то соотношения
а
и
аn-тангенциальное
и нормальное ускорение, то соотношения
а![]() >0
и а n=
0 справедливы для:
>0
и а n=
0 справедливы для:
Варианты ответов:
1) равномерного и прямолинейного движения;
2) ускоренного и прямолинейного движения;
3) равномерного и криволинейного движения;
4) ускоренного и криволинейного движения;
5) замедленного и криволинейного;
6) равномерного движения по окружности.
Решение.
Нормальное
ускорение ап
характеризует
изменение скорости по направлению.
Следовательно, если аn
=
0, то скорость по направлению не
изменяется, и движение будет прямолинейным.
Тангенциальное ускорение а![]() характеризует изменение скорости по
модулю (или величине). Поэтому, если
а
характеризует изменение скорости по
модулю (или величине). Поэтому, если
а![]() >0,
то
скорость по модулю возрастает, и
движение будет ускоренным.
>0,
то
скорость по модулю возрастает, и
движение будет ускоренным.
Ответ: вариант 2.
Тест 1 - 2
Точка М движется по спирали с постоянной по величине скоростью в направлении, указанном стрелкой. При этом величина полного ускорения...
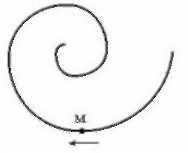
Варианты ответов:
1) увеличивается ;
2) не изменяется;
3) уменьшается.
Решение.
Полное
ускорение равно векторной сумме
нормального и тангенциального ускорения:
![]() =
=
![]() п +
п +
![]() τ
. Нормальное ускорение характеризует
изменение скорости по направлению и
равно a
n
=
v
2/R,
где v
– скорость точки, R
– радиус кривизны траектории. Так как
по условию задачи v
= const,
а R
при движении, показанном на рисунке (т.
е. по часовой стрелке) уменьшается, то
a
n
увеличивается.
Другая составляющая ускорения -
тангенциальное ускорение аτ
характеризует изменение скорости по
величине (или по модулю) и равно
производной от скорости по времени: а
τ
= dv/dt.
Так как скорость v
= const,
то её производная равна нулю и а τ
=0. Тогда а =a
n
,
т.е. полное ускорение по модулю равно
нормальному ускорению. Следовательно,
полное ускорение увеличивается.
τ
. Нормальное ускорение характеризует
изменение скорости по направлению и
равно a
n
=
v
2/R,
где v
– скорость точки, R
– радиус кривизны траектории. Так как
по условию задачи v
= const,
а R
при движении, показанном на рисунке (т.
е. по часовой стрелке) уменьшается, то
a
n
увеличивается.
Другая составляющая ускорения -
тангенциальное ускорение аτ
характеризует изменение скорости по
величине (или по модулю) и равно
производной от скорости по времени: а
τ
= dv/dt.
Так как скорость v
= const,
то её производная равна нулю и а τ
=0. Тогда а =a
n
,
т.е. полное ускорение по модулю равно
нормальному ускорению. Следовательно,
полное ускорение увеличивается.
Ответ: вариант 1.
Тест 1 – 3
Точка движется по окружности с постоянным тангенциальным ускорением. Если проекция тангенциального ускорения на направление скорости положительна, то величина нормального ускорения…
Варианты ответов:1) уменьшается; 2) не изменяется; 3) увеличивается.
Решение.
Нормальное ускорение характеризует изменение скорости по направлению и равно a n = v 2/R, где v – скорость точки, R – радиус кривизны траектории. Так как по условию задачи точка движется по окружности, то R = const. Тангенциальное ускорение характеризует изменение скорости по величине (или по модулю) и равно а τ = dv/dt . По условию а τ= const и проекция тангенциального ускорения на направление скорости положительна. Следовательно, движение по окружности будет равноускоренным. Поскольку при равноускоренном движении скорость по модулю увеличивается, то величина нормального ускорения a n по модулю также увеличивается.
Ответ: вариант 3.
Тест 1 – 4
Материальная
точка М движется по окружности со
скоростью ![]() .
На рис. 1 показан график зависимости
vτ
от времени (
.
На рис. 1 показан график зависимости
vτ
от времени (![]() -единичный вектор положительного
направления, vτ
- проекция
-единичный вектор положительного
направления, vτ
- проекция ![]() на это направление). На рис.2 укажите
направление вектора полного ускорения.
на это направление). На рис.2 укажите
направление вектора полного ускорения.
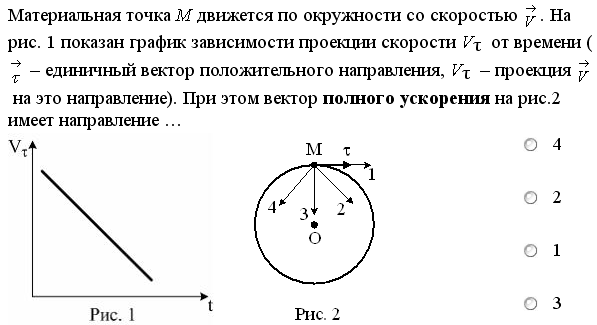

Варианты ответов:
1) Направление 1; 2) Направление 2; 3) Направление 3; 4) Направление 4.
Решение.
Полное
ускорение тела складывается из векторной
суммы тангенциального ускорения ![]() τ
,
характеризующего изменение
скорости
по модулю (или величине), и нормального
ускорения
τ
,
характеризующего изменение
скорости
по модулю (или величине), и нормального
ускорения ![]() n
,
характеризующего изменение скорости
по направлению. Рассмотрим, как направлены
вектора
n
,
характеризующего изменение скорости
по направлению. Рассмотрим, как направлены
вектора ![]() τ
и
τ
и ![]() n
.
При
равнопеременном движении вектор
тангенциального ускорения совпадает
по направлению с вектором скорости,
если движение равноускоренное, и
противоположен ей, если движение
равнозамедленное. Вектор нормального
ускорения перпендикулярен вектору
скорости.
n
.
При
равнопеременном движении вектор
тангенциального ускорения совпадает
по направлению с вектором скорости,
если движение равноускоренное, и
противоположен ей, если движение
равнозамедленное. Вектор нормального
ускорения перпендикулярен вектору
скорости.
Из
рис. 1 следует, что модуль вектора
скорости линейно убывает со временем.
Следовательно, движение будет
равнозамедленным, и вектор тангенциального
ускорения будет противоположен по
направлению вектору скорости vτ.
Так как скорость направлена по касательной
к траектории (направление 1 на рис. 2),
то направление тангенциального ускорения
![]() τ
при равнозамедленном движении будет
противоположно направлению 1.
τ
при равнозамедленном движении будет
противоположно направлению 1.
При
движении тела по окружности скорость
изменяется по направлению, и нормальное
ускорение
![]() n
будет
направлено к центру окружности
(направление 3 на рис.2). Результирующее
ускорение, равное векторной сумме
n
будет
направлено к центру окружности
(направление 3 на рис.2). Результирующее
ускорение, равное векторной сумме ![]() =
=
![]() τ
+
τ
+
![]() n
,
будет иметь направление 4.
n
,
будет иметь направление 4.
Ответ: вариант 4.
Тест 1 – 5
Материальная
точка М
движется
по окружности со скоростью
![]() .
На
рис. 1 показан график зависимости vτ
от времени (
.
На
рис. 1 показан график зависимости vτ
от времени (![]() - единичный вектор положительного
направления, vτ
-
проекция
- единичный вектор положительного
направления, vτ
-
проекция
![]() на
это направление). На рис.2 укажите
направление силы, действующей на точку
М в момент времени t1.
на
это направление). На рис.2 укажите
направление силы, действующей на точку
М в момент времени t1.


Варианты ответов:
1) Направление 1; 2) Направление 2; 3) Направление 3; 4) Направление 4.
Решение
Согласно
второму закону Ньютона, ускорение
пропорционально результирующей силе,
действующей на тело. Полное ускорение
тела складывается из векторной суммы
тангенциального ускорения ![]() τ,
которое
характеризует изменение
скорости
по модулю, и нормального ускорения
τ,
которое
характеризует изменение
скорости
по модулю, и нормального ускорения
![]() n
,
характеризующего изменение скорости
по направлению. Из рис.1 следует, что
для момента времени t
1
скорость по модулю линейно возрастает.
Следовательно, движение будет
равноускоренным, и вектор тангенциального
ускорения
n
,
характеризующего изменение скорости
по направлению. Из рис.1 следует, что
для момента времени t
1
скорость по модулю линейно возрастает.
Следовательно, движение будет
равноускоренным, и вектор тангенциального
ускорения ![]() τ
будет совпадать по направлению с
вектором скорости
τ
будет совпадать по направлению с
вектором скорости ![]() τ
(направление 1 на рис. 2) .
τ
(направление 1 на рис. 2) .
При
движении тела по окружности скорость
изменяется по направлению, и нормальное
ускорение ![]() n
будет
направлено к центру окружности
(направление 3 на рис.2). Результирующее
ускорение равно векторной сумме
n
будет
направлено к центру окружности
(направление 3 на рис.2). Результирующее
ускорение равно векторной сумме ![]() =
=
![]() τ+
τ+
![]() n
и будет
иметь направление 2. Следовательно,
результирующая сила также будет иметь
направление
2.
Ответ:
вариант 2.
n
и будет
иметь направление 2. Следовательно,
результирующая сила также будет иметь
направление
2.
Ответ:
вариант 2.
Тест 1 – 6
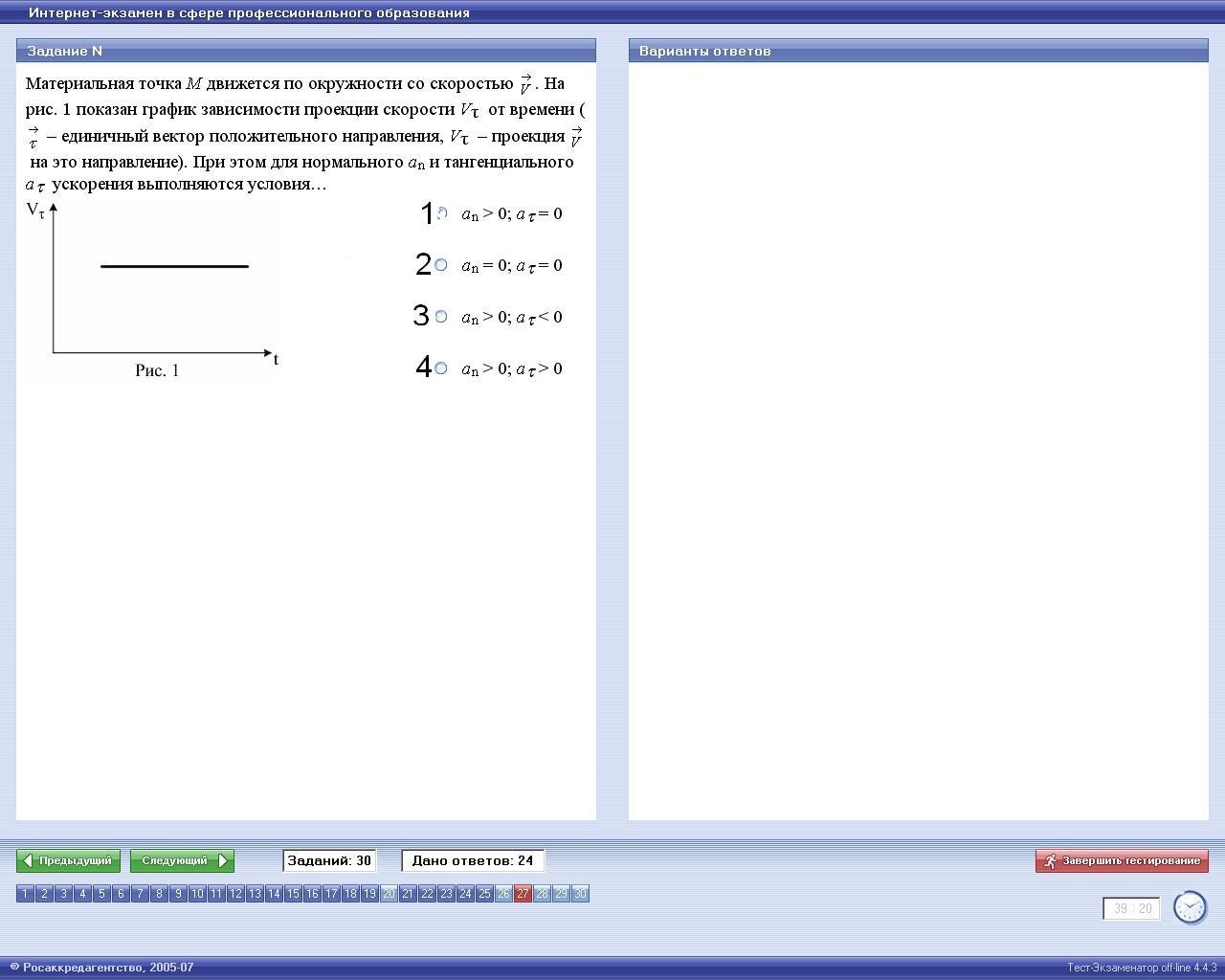 Материальная
точка М
движется
по окружности со скоростью . На
Материальная
точка М
движется
по окружности со скоростью . На
рис.
1 показан график зависимости проекции
скорости vτ
от времени,
где ![]() -
единичный вектор положительного
направления vτ
-
проекция
-
единичный вектор положительного
направления vτ
-
проекция
![]() .на
это направление. При этом для нормального
аn
и
тангенциального аτ
ускорения
выполняются условия...
.на
это направление. При этом для нормального
аn
и
тангенциального аτ
ускорения
выполняются условия...
Варианты ответов:
1) аn>0; аτ= 0; 2) an = 0; aτ= 0;
3) аn>0; аτ<0. 4) ап>0; аτ>0.
Решение
Нормальное ускорение аn характеризует изменение скорости по направлению. Если точка движется по окружности, то её скорость изменяется по направлению, следовательно, аn> 0. Тангенциальное ускорение аτ характеризует изменение скорости по модулю (или величине). Из рис. 1 следует, что скорость по модулю не изменяется, т.е. тангенциальное ускорение аτ=0. Следовательно, аn>0, аτ = 0. Ответ: вариант 1.
Тест 1 - 7
Тело массой 2 кг поднято над Землёй. Его потенциальная энергия равна 400 Дж. Если на поверхности Земли его потенциальная энергия равна нулю и силами сопротивления воздуха можно пренебречь, скорость, с которой оно упадёт на Землю составит…
Варианты ответов:
1) 14 м/с; 2) 20 м/с; 3) 10 м/с; 4) 40 м/с.
Решение
Поскольку
силами сопротивления воздуха можно
пренебречь, то нужно применить закон
сохранения энергии, согласно которому,
потенциальная энергия тела, поднятого
над Землёй, равна его кинетической
энергии в конце падения: W
p=
Wk.
Кинетическая энергия тела
равна
Wk
= mv
2/2.
Отсюда v
=
![]() . После численной подстановки получим:
v
= 20 м/с.
. После численной подстановки получим:
v
= 20 м/с.
Ответ: вариант 2.
 Тест
1 – 8
Тест
1 – 8
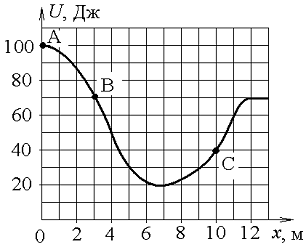
Небольшая шайба начинает движение без начальной скорости по гладкой ледяной горке из точки А. Сопротивление воздуха пренебрежимо мало. Зависимость потенциальной энергии шайбы от координаты х изображена на графике U=U(x).
Скорость шайбы в точке С … Варианты ответов:
1)
в
![]() раз
больше, чем в точке В;
раз
больше, чем в точке В;
2) в 4 раза больше, чем в точке В;
3)
в
![]() раза
больше, чем в точке В;
раза
больше, чем в точке В;
4) в 2 раза больше, чем в точке В.
Решение.
Поскольку силами сопротивления воздуха и силами трения шайбы о лед можно пренебречь, то нужно применить закон сохранения энергии, и полную механическую энергию замкнутой системы считать постоянной. Так как полная механическая энергия системы равна сумме кинетической и потенциальной, то W = Wк + WP = const. Потенциальную энергию можно найти из графика, приведённого на рисунке, а кинетическую найти как разность между полной энергией и потенциальной: Wк = W - WP . Следовательно, в точке А энергия равна:
W= WP =100 Дж, Wк = 0. В точке В WP =70 Дж, Wк В= 100 -70 = 30 Дж.
В точке С WP =40 Дж, Wкс = 100 -40 = 60 Дж.
Чтобы сравнить скорости в точках С и В, нужно найти отношение их кинетических энергий. Учитывая, что кинетическая энергия равна W k= m v 2/2, получим:
![]() =
= 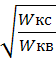 =
= ![]() =
= ![]() .
Таким образом,
скорость
шайбы в точке С
в
.
Таким образом,
скорость
шайбы в точке С
в
![]() раз
больше,
чем в точке В.
Ответ:
вариант
1.
раз
больше,
чем в точке В.
Ответ:
вариант
1.
Тест 1 – 9
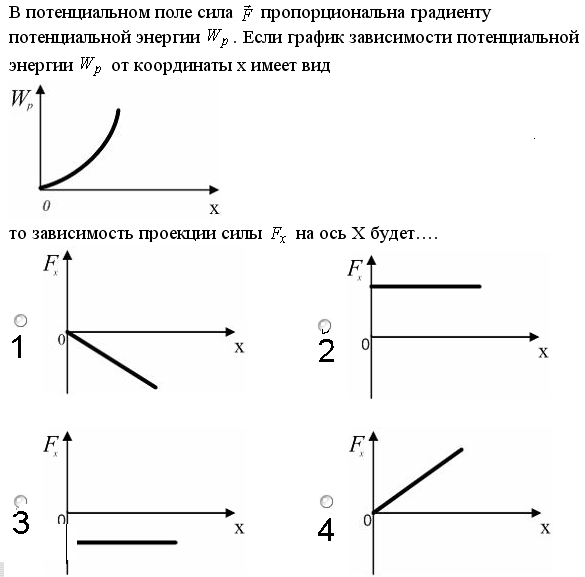 В
потенциальном поле сила
пропорциональна
градиенту потенциальной энергии WP.
Если график зависимости потенциальной
энергии WP
от
координаты х имеет вид, представленный
на рисунке, то зависимость проекции
силы Fх
на ось Оx будет…
В
потенциальном поле сила
пропорциональна
градиенту потенциальной энергии WP.
Если график зависимости потенциальной
энергии WP
от
координаты х имеет вид, представленный
на рисунке, то зависимость проекции
силы Fх
на ось Оx будет…
Варианты ответов:
