2 Электричество

Основные формулы и определения

● Сила взаимодействия F между двумя неподвижными точечными зарядами q ₁ и q ₂ вычисляется по закону Кулона:

F = k∙│q₁│∙│q₂│/ r²,

где k - коэффициент пропорциональности, r – расстояние между зарядами.

● Напряженность электрического поля – это силовая характеристика, определяемая силой, действующей на единичный точечный положительный заряд q₀ , помещенный в данную точку поля:

= /q₀.

Линии напряженности электрического поля начинаются на положительных зарядах и заканчиваются на отрицательных зарядах или уходят в бесконечность, то есть силовые линии разомкнуты.

● По теореме Гаусса поток вектора напряженности электрического поля через замкнутую поверхность равен алгебраической сумме зарядов, заключенных внутри поверхности, делённой на электрическую постоянную и диэлектрическую проницаемость среды.

● Напряженность электрического поля равна градиенту потенциала, взятому с обратным знаком:

= - grad φ.

Связь между проекцией напряженности электрического поля на ось x и потенциалом даётся уравнением:

Е_х = - d φ/dx.

● Электростатическое поле является потенциальным. Работа в потенциальном поле сил может быть представлена как разность потенциальных энергий или как произведение заряда q на разность потенциалов:

А = W₁ – W₂ = q(φ₁ – φ₂ ).

● По закону Ома для однородного участка цепи:

R = U/I,

где U – напряжение на участке цепи, I – сила тока в цепи, R –сопротивление участка цепи.

Сопротивление однородного проводника:

R = ρ∙ℓ/ S,

где ρ –удельное сопротивление проводника, ℓ- длина участка проводника, S – площадь поперечного сечения.

● Зависимость плотности тока ј от напряженности электрического поля E подчиняется закону Ома в дифференциальной форме:

ј = σ · E,

где σ – удельная проводимость. Удельной проводимостью называется величина, обратная удельному сопротивлению:

σ = 1/ ρ.

● Мощность постоянного тока N равна произведению силы тока I на напряжение U:

N = I·U.

● Закон Ома для полной цепи:

ε = I∙R + I·r,

где ε – ЭДС источника тока, I – сила тока в цепи, R – внешнее сопротивление, r – внутреннее сопротивление источника тока.

Тест 2 -1

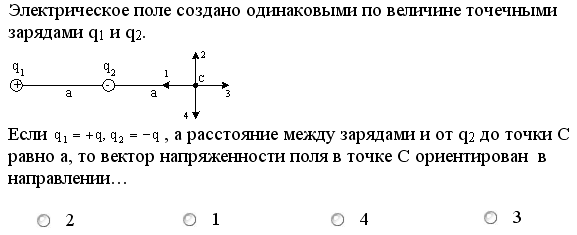
Электрическое поле создано одинаковыми по величине точечными зарядами q₁ и q₂. Если q₁ = +q , q₂ = -q, a расстояние между зарядами и от заряда q₂ до точки С равно а, то вектор напряженности поля в точке С ориентирован в направлении...

Варианты ответов:

1) в направлении 1;

2) в направлении 2;

3) в направлении 3;

4) в направлении 4.

Решение.

Напряженность электрического поля – это силовая характеристика, определяемая силой, действующей на единичный точечный положительный заряд, помещенный в данную точку поля: = / q₀. Для того чтобы определить направление вектора напряженности, надо в данную точку поля (точку наблюдения) поместить воображаемый единичный положительный заряд, тогда вектор силы, действующий на него, укажет направление вектора напряженности. Следовательно, со стороны заряда +q ₁ на пробный заряд +q _0, помещенный в точку С, будет действовать сила отталкивания, и вектор напряженности ₁ будет иметь направление 3, а со стороны отрицательного заряда -q ₂ будет действовать сила притяжения, и вектор ₂ будет иметь направление 1. Результирующая напряженность находится по принципу суперпозиции:

= ₁ + ₂ . В скалярной форме: E = E ₁ - E ₂. Модуль вектора напряженности электрического поля точечного заряда равен:

E = k∙q /r²,

где k - коэффициент пропорциональности r – расстояние от точечного заряда до точки наблюдения. Так как расстояние от заряда q₁ до точки С в два раза больше, чем от заряда q₂, то E ₁ < E ₂ , и вектор E результирующей напряженности электрического поля будет ориентирован в направлении 1.

Ответ: вариант 1.

Тест 2 – 2

Точечный заряд +q находится в центре сферической поверхности. Если добавить заряд +q за пределами сферы, то поток вектора напряженности электростатического поля через поверхность сферы...

Варианты ответов: