
Контрольная работа №1
102. Уравнения
движения двух материальных точек по
прямой:
![]() ,
где
,
где![]() = 12
м/с,
= 12
м/с,![]() ,
,![]() ,
где
,
где![]() = 2
м/с,
= 2
м/с,![]() .
В какой момент времени скорости этих
точек будут одинаковыми? Чему равны
скорости и ускорения точек в этот момент?
.
В какой момент времени скорости этих
точек будут одинаковыми? Чему равны
скорости и ускорения точек в этот момент?
Дано:
![]()
![]()
![]() = 12
м/с
= 12
м/с
![]()
![]() = 2
м/с
= 2
м/с
![]()
v1 = v2 = v
t=? v=? a1 =? а2 = ?
Решение:
Модуль мгновенной скорости находим как производную от координаты по времени:
![]()
![]()
![]()
Приравниваем скорости двух точек и находим в какой момент времени это произойдет
![]()
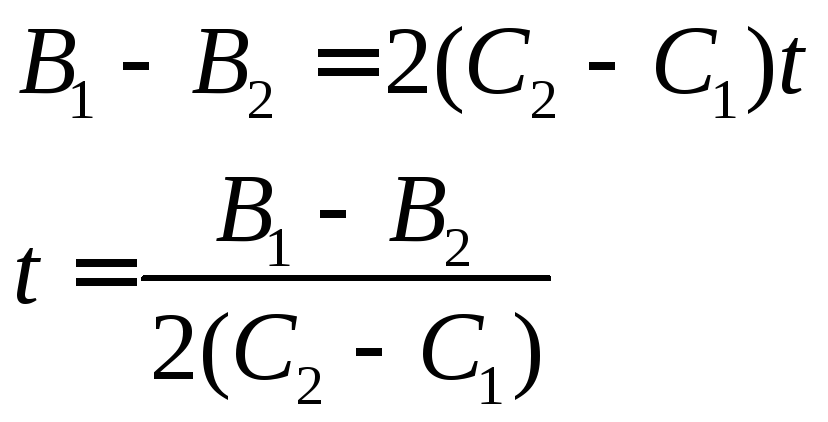
![]() с
с
Скорости в этот момент будут равны
![]()
![]() м/с
м/с
Ускорение есть производная скорости по времени
![]()
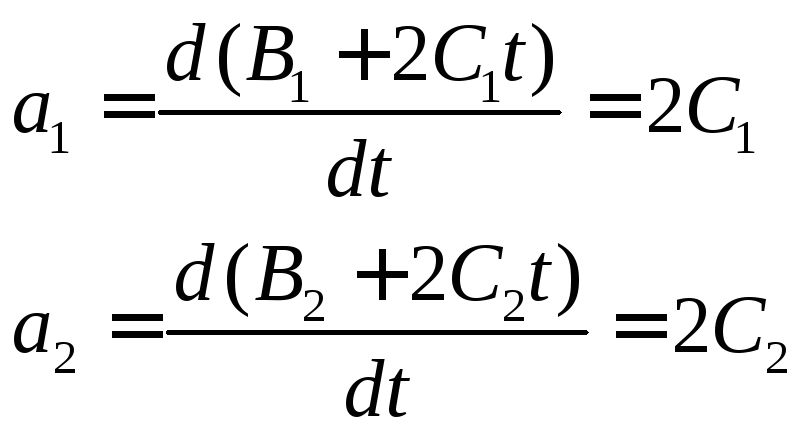
Таким образом, ускорения точек постоянны во времени и равны
![]() м/с2
м/с2
![]() м/с2
м/с2
Ответ:
![]() с,
с,![]() м/с,
м/с,![]() м/с2,
м/с2,
![]() м/с2.
м/с2.
112. На горизонтальной поверхности лежит тело массой 5 кг. Какой путь пройдет это тело за 1 с, если к нему приложить силу 50 Н, образующую угол 60 с горизонтом? Коэффициент трения между телом и поверхностью принять равным 0,2.
Дано:
m = 5 кг
t = 1 c
F = 50 H
α = 60
μ = 0,2
L=?
Решение:
На тело действуют
силы: сила тяжести
![]() ,
сила реакции опоры
,
сила реакции опоры![]() ,
сила трения
,
сила трения![]() ,
сила
,
сила![]() .
Изобразим их на чертеже, направим оси
координат – х – вдоль плоскости горизонта
в сторону направления проекции силыF,
у – перпендикулярно плоскости вверх.
.
Изобразим их на чертеже, направим оси
координат – х – вдоль плоскости горизонта
в сторону направления проекции силыF,
у – перпендикулярно плоскости вверх.
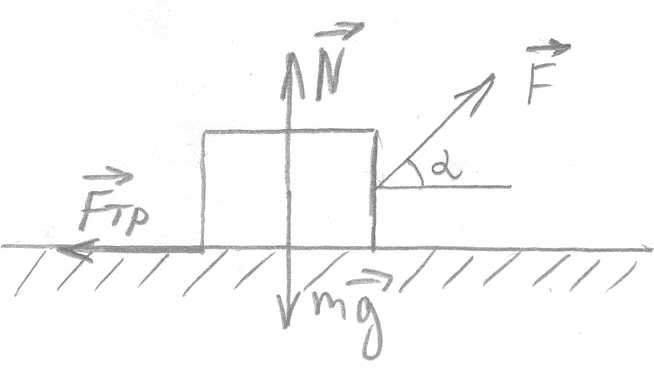
По второму закону Ньютона
![]()
Спроецируем равенство на оси координат
Х:
![]() (1)
(1)
Y:
![]()
Из последнего
равенства имеем
![]() .
.
Сила трения равна
![]()
Подставим в (1)
![]()
Выразим ускорение
![]()
![]()
Найдем пройденный путь. Движение равноускоренное. Начальная скорость и расстояние равны 0. Тогда скорость равна
![]()
Пройденное расстояние
![]()
Проверим размерность
[L]= с2·[(кг·м/с2)/кг - м/с2] = м
Вычислим
![]() м
м
Ответ: 2,4 м.
122. Снаряд, летевший со скоростью 400 м/с, разорвался на два осколка. Меньший осколок, масса которого составляет 40% от массы снаряда, полетел в противоположном направлении со скоростью 150 м/с. Определить скорость большого осколка (по величине и направлению).
Дано:
v = 400 м/с
m1 = 0,4m
u1 = 150 м/с
u2=?
Решение:
Сопротивлением
воздуха пренебрежем. Считаем, что снаряд
находится в горизонтальном полете,
появлением вертикальной составляющей
скорости в результате действия силы
тяжести также пренебрежем. В этом случае
система замкнутая, суммарный импульс
сохраняется. Запишем закон сохранения
импульса
![]() .
Исходя из того, что векторы скоростей
.
Исходя из того, что векторы скоростей![]() и
и![]() противонаправлены, очевидно, что вектор
скорости
противонаправлены, очевидно, что вектор
скорости![]() также параллелен первым двум векторам.
Примем, что он сонаправлен
также параллелен первым двум векторам.
Примем, что он сонаправлен![]() .
.
Сделаем чертеж
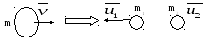

Спроецируем закон сохранения импульса на направление скорости полета снаряда.
![]()
Найдем выражение для скорости большей части снаряда.
![]()
Учтем, что
![]()
![]()
Вычислим ![]() м/с
м/с
Поскольку скорость получилась положительной, следовательно, направление вектора скорости выбрано верно.
Ответ: 767 м/с.
132. Найти работу, совершаемую при подъеме груза массой 10 кг по наклонной плоскости с углом наклона 45 на расстояние 2 м, если время подъема – 2 с, а коэффициент трения = 0,1.
Дано:
m = 10 кг
α = 45
L = 2 м
t = 2 с
= 0,1
А = ?
Решение:
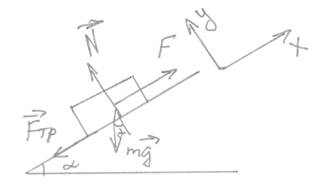
На тело действуют
силы: сила тяжести
![]() ,
сила реакции опоры
,
сила реакции опоры![]() ,
сила трения
,
сила трения![]() и внешняя сила
и внешняя сила![]() ,
которая и будет совершать работу.
Изобразим их на чертеже, направим оси
координат –х – вдоль плоскости вверх,
у – перпендикулярно плоскости вверх.
,
которая и будет совершать работу.
Изобразим их на чертеже, направим оси
координат –х – вдоль плоскости вверх,
у – перпендикулярно плоскости вверх.
Тогда по второму закону Ньютона
![]()
Спроецируем равенство на оси координат
Х:
![]()
Y:
![]()
Из последнего
равенства имеем
![]() .
.
Подставим в первое уравнение и выразим ускорение тела
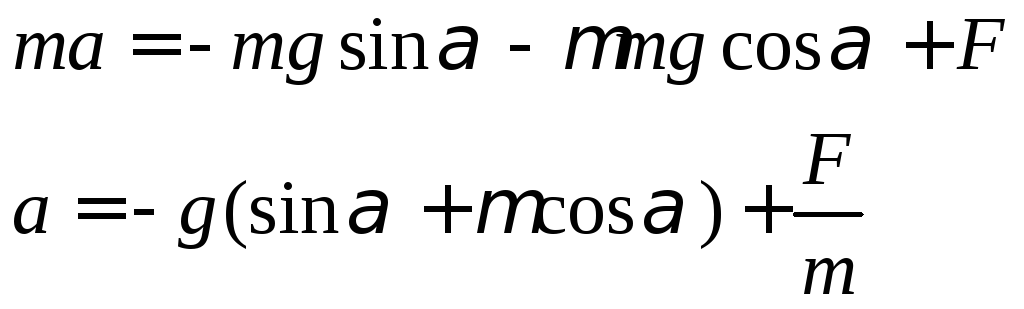
Ускорение, с котором будет двигаться тело, найдем из условия для времени подъема. Для равноускоренного движения
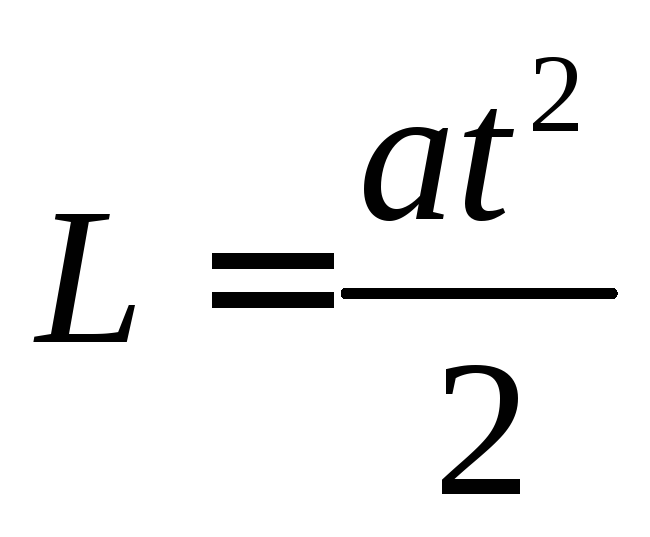
Отсюда ускорение
тела равно
![]() .
.
Приравняем выражения для ускорения и выразим действующую на тело силу.
![]()
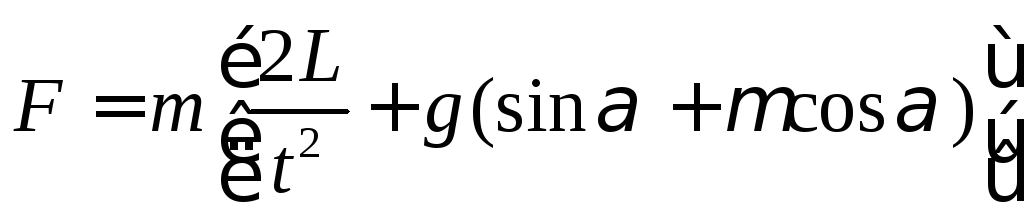
По определению
работа силы F
равна
![]()
![]() - перемещение тела,
- перемещение тела,
![]() - направление между вектором силы и
вектором перемещения.
- направление между вектором силы и
вектором перемещения.
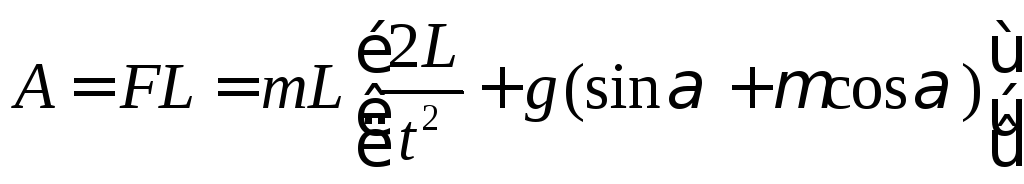
Проверим размерность
[А]=кг·м·м/с2 = Дж
 Дж
Дж
Ответ: 172 Дж.
142. На барабан
радиусом 20 см, момент инерции которого
равен 0,1
![]() ,
намотан шнур, к которому привязан груз
массой 0,5 кг. До начала вращения барабана
высота груза над полом равна 1 м. Найти:
1) через сколько времени груз опустится
до пола; 2) кинетическую энергию груза
в момент удара о пол. Трением пренебречь.
,
намотан шнур, к которому привязан груз
массой 0,5 кг. До начала вращения барабана
высота груза над полом равна 1 м. Найти:
1) через сколько времени груз опустится
до пола; 2) кинетическую энергию груза
в момент удара о пол. Трением пренебречь.
Дано:
R = 20 см = 0,2 м
I = 0,1
![]()
m=0,5 кг
Н = 1 м
t = ? WK = ?
Решение:
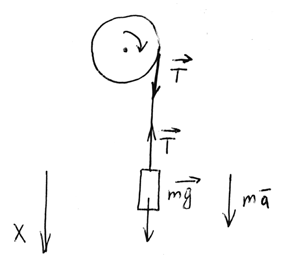
Считаем шнур невесомым и нерастяжимым, тогда сила натяжения шнура Т одинакова во всех точках
Второй закон Ньютона для груза (проецируем на ось ox):
![]() (1)
(1)
Угловое ускорение
маховика будет равно
![]() ,
(2) гдеR-радиус
маховика.
,
(2) гдеR-радиус
маховика.
По закону изменения момента импульса системы
![]() ,
,
где L-
момент импульса системы,
![]() - момент внешних сил, действующих на
систему (силаT)
- момент внешних сил, действующих на
систему (силаT)
![]() ,
где
,
где
![]() - угловая скорость маховика. С учетом
того, чтоI
постоянно
- угловая скорость маховика. С учетом
того, чтоI
постоянно
![]()
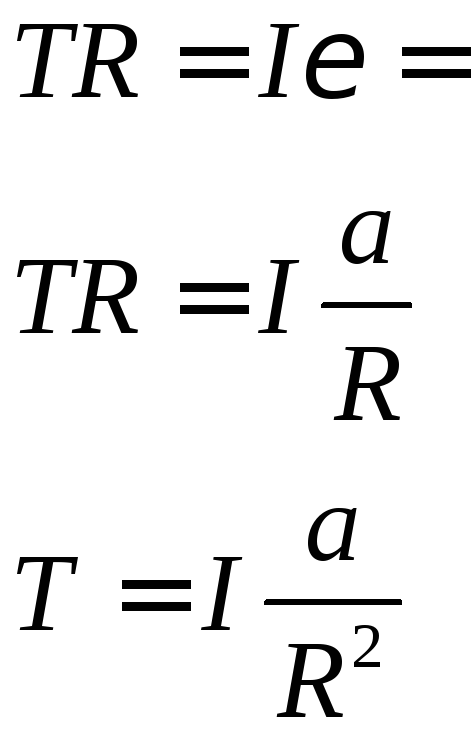
Подставляем в (1) и находим ускорение
![]()
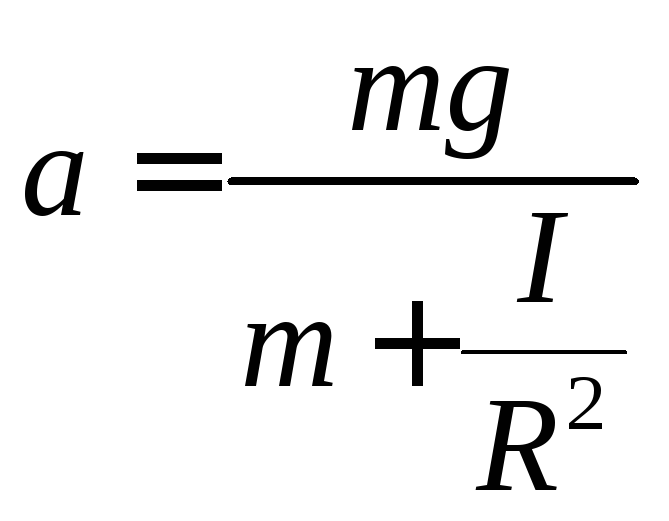
Для равноускоренного движения зависимость пройденного расстояния от времени
![]()
Отсюда находим время опускания груза
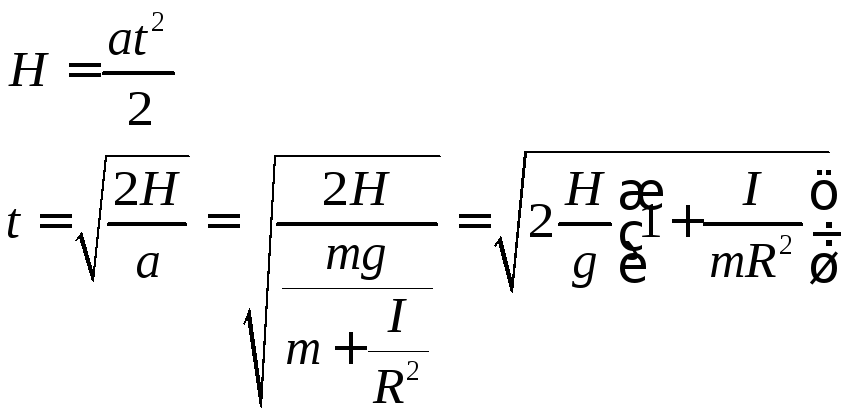
Вычислим
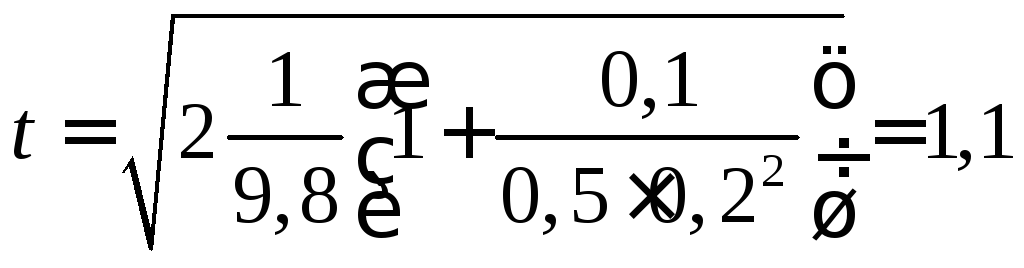 с
с
Если скорость груза в начальный момент времени равна нулю, то в момент касания пола она будет равна
![]() .
.
Кинетическая энергия груза в момент касания
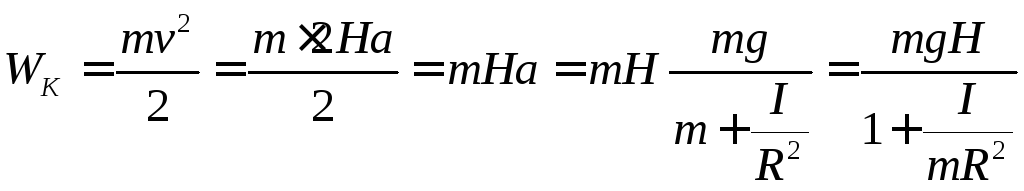
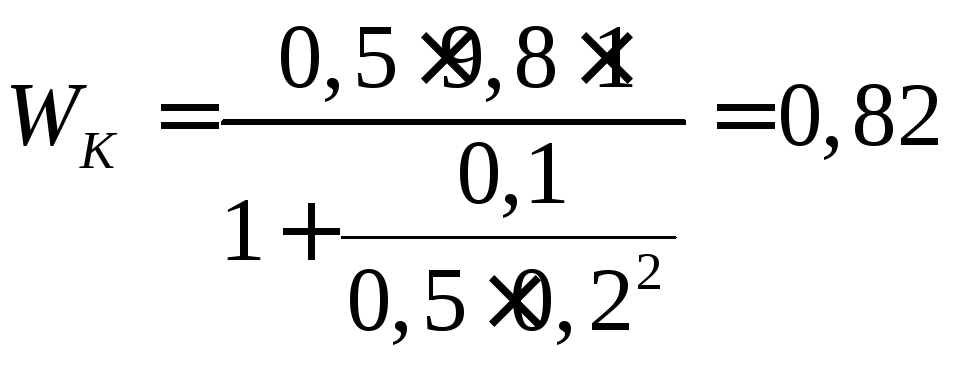 Дж
Дж
Ответ: 0,82 Дж.
152. Определить высоту наклонной плоскости, если линейная скорость центра шара, скатившегося без скольжения с наклонной плоскости равна 2,65 м/с. Начальная скорость шара равна нулю.
Дано:
v= 2,65 м/с
h =?
Решение:
Движение шара складывается из поступательного и вращательного движения шара. Следовательно,
Wk= Wk пост+ Wk вр
Кинетическая энергия поступательного движения
Wk
пост =
![]()
![]() - скорость центра
масс, т.е. центра шара,
- скорость центра
масс, т.е. центра шара,
![]() - масса шара.
- масса шара.
Кинетическая энергия вращательного движения
Wk
вр =
![]()
![]() - момент инерции
шара,
- момент инерции
шара,
![]() - угловая скорость вращения.
- угловая скорость вращения.
Изобразим движение шара. Линейная скорость движения точек шара, которые попеременно соприкасаются с поверхностью, одинакова. Тогда суммарные мгновенные значения скоростей равны:
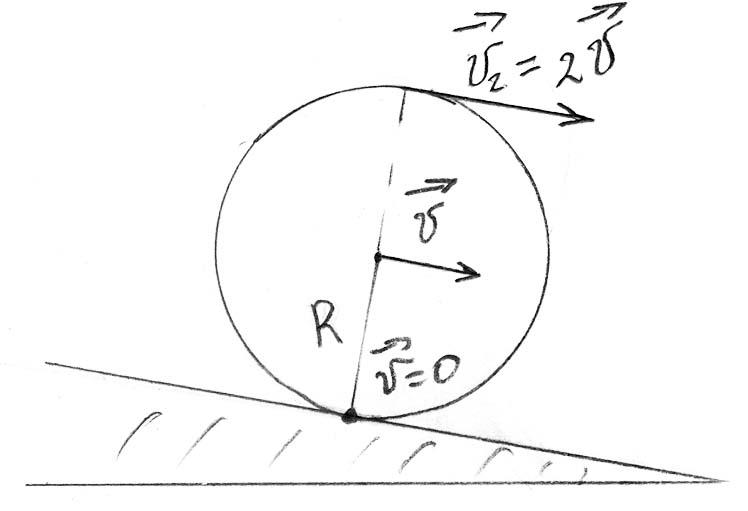
Обозначим радиус шара R. Тогда
![]()
Для сплошного шара
![]()
Wk=
![]()
Система замкнутая. По закону сохранения энергии
Wk
=![]()
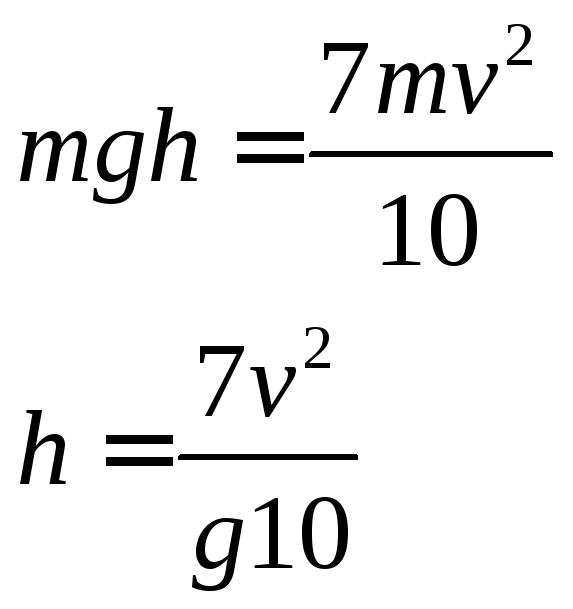
Проверим размерность
![]()
![]() м
м
Ответ: 0,50 м.
