
- •Содержание
- •1. Теоретические основы построения гмм аналитическим способом.
- •1.1. Обоснование выбора вариантной системы взаимного ориентирования снимков
- •1.2. Вывод и решение строгого уравнения взаимного ориентирования снимков
- •1.2.1. Вывод строгого уравнения взаимного ориентирования в вариантной системе координат
- •1.2.2. Решение строгого уравнения взаимного снимков в вариантной системе
- •1.3. Вывод приближенного уравнения взаимного ориентирования
- •1.4. Вывод формул определения элементов взаимного ориентирования в вариантной системе
- •1.5. Вывод формул прямой фотограмметрической засечки
- •1.6. Внешнее ориентирование модели
- •1.7. Вывод формул априорной оценки точности построения геометрической модели местности в вариантной системе
1.2.2. Решение строгого уравнения взаимного снимков в вариантной системе
Исходным уравнением для определения элементов взаимного ориентирования является условие компланарности соответственных лучей (1.5). Это уравнение является нелинейным по отношению к неизвестным
1' ,1’, 1’, , . Для определения неизвестных используется итерационный метод.
Представим уравнение (1.5) в виде
φ( 1' , 1’, 1’, , )= cos cos ( Y1’Z2’ – Z1’Y2’) - cos sin ( X1’Z2’ – Z1’X2’) +
+
(1.12)
З
(1.13)
1'0 = 1’0=1’0= 0 = 0=0 .
Разложим функцию (1.12) в ряд Тейлора, ограничиваясь величинами первого порядка малости для того, чтобы уравнение (1.5) стало линейным.
Запишем в общем виде разложение функции (1.12) в ряд Тейлора:
φ( 1'
,1’,
1’,
,
)= φ(1'0,
1’0,
1’0,
0,
0)
+
 δ1'
+
δ1'
+
+
![]()
 δ1’+
δ1’+
![]() δ2’+
δ2’+
![]() δ
+
δ
+
+
(1.14)![]() δ
.
δ
.
В формуле (1.14): φ( 1' ,1’, 1’, , )-истинное значение функции (1.12),
φ(1'0, 1’0, 1’0, 0, 0)- значение функции, вычисленное через приближенные значения элементов взаимного ориентирования 1'0, 1’0, 1’0, 0, 0,
 ,
,
 ,
,![]() ,
,![]() ,
,![]() -первые
производные от функции (1.12) по элементам
взаимного ориентирования .
-первые
производные от функции (1.12) по элементам
взаимного ориентирования .
![]() δ1',δ1’,
δ1’,
δ,
δ-
поправки к приближенным значениям
элементов взаимного ориентирования,
являются неизвестными в уравнение
(1.14)
δ1',δ1’,
δ1’,
δ,
δ-
поправки к приближенным значениям
элементов взаимного ориентирования,
являются неизвестными в уравнение
(1.14)
Найдем первую производную от функции (1.12) по 1' :
(1.15)
-sin(Y2’Z1’) ;
Найдем первую производную от функции (1.12) по 1’:






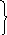


 =
cos
cos
Z2’
b2’(x1-x0)-b1’(y1-y0)
-
=
cos
cos
Z2’
b2’(x1-x0)-b1’(y1-y0)
-
- Y2’ c2’(x1-x0)-c1’(y1-y0) - cos sin Z2’ a2’(x1-x0)+ a1’(y1-y0) -
-

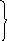


 X2’
c2’(x1-x0)-c1’(y1-y0)
+ sin
Y2’
a2’(x1-x0)
+ a1’(y1-y0)
-
X2’
c2’(x1-x0)-c1’(y1-y0)
+ sin
Y2’
a2’(x1-x0)
+ a1’(y1-y0)
-
(1.16)



- X2’ b2’ (x1-x0) – b1’ ( y1-y0) ;
Н айдем
первую производную от функции (1.12) по1’
:
айдем
первую производную от функции (1.12) по1’
:
![]()







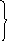
 σ1’=
cos
cos
Z
2’
b3’
sin1’
( x1-x0)+
b3’cos1’
(y1-y0)
+ + cos1’
f - Y2’
c3’
sin1’
(x1-x0)-
f - c3’
cos1’
(y1-y0)
– b3’
cosα1’
f
-
σ1’=
cos
cos
Z
2’
b3’
sin1’
( x1-x0)+
b3’cos1’
(y1-y0)
+ + cos1’
f - Y2’
c3’
sin1’
(x1-x0)-
f - c3’
cos1’
(y1-y0)
– b3’
cosα1’
f
-


 -cos
sin
Z
2’
a3’
sin1’
(x1-x0)
+ a3’
cos1’
(y1-y0)+
b3’
sin α1’f
-
-cos
sin
Z
2’
a3’
sin1’
(x1-x0)
+ a3’
cos1’
(y1-y0)+
b3’
sin α1’f
-
-

 X2’
c3’
sin1’(x1-x0)-
c3’
cos1’(y1-y0)
- cosα1’
f +
X2’
c3’
sin1’(x1-x0)-
c3’
cos1’(y1-y0)
- cosα1’
f +
+ (1.17)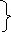

 sin
Y2’
a3’sin1’(x1-x0)
+ a3’cos1’
( y1-y0)
+ b3’
sin α1’
f -
sin
Y2’
a3’sin1’(x1-x0)
+ a3’cos1’
( y1-y0)
+ b3’
sin α1’
f -
- X2’ b3’ sin1’(x1-x0) + b3’cos1’(y1-y0) + cos1’ f
Найдем первую производную от функции (1.12) по :
(1.18)![]()
+ cos( X1’Y2’ – Y1’X2’) ;
Н
(1.19)![]() =
-cos
sin
( Y1’Z2’-Z1’Y2’)
- cos
cos(X1’Z2’-Z1’X2’);
=
-cos
sin
( Y1’Z2’-Z1’Y2’)
- cos
cos(X1’Z2’-Z1’X2’);
Обозначим в (1.14) первые производные в виде коэффициентов:

 =
a
=
a
(1.20)
: =b
=b
![]() =
c
=
c
![]() =
d
=
d
![]() =
e
=
e
Перенесем φ( 1' ,1’, 1’, , ) в правую часть выражения (1.14):
φ
(1.21)
где l- свободный член.
У
(1.22)
aδ1' + bδ1’ + cδ2’ + dδ + eδ + l = 0 ,
Уравнение (1.22) будет линейным по отношению к неизвестным δ1',δ1’, δ1’, δ, δ.
Если число уравнений больше пяти , то возникает задача уравнивания и вместо уравнений вида (1.22) будет иметь место система уравнений поправок:
 a1δ1'+b1δ1’+c1δ1’+d1δ+e1δ=V1
a1δ1'+b1δ1’+c1δ1’+d1δ+e1δ=V1
(1.23)
,
. . . . . . . . . . . . . . . . .
anδ1'+bnδ1’+cnδ1’+dnδ+enδ=Vn
n-число уравнений поправок, равное числу точек стереопары, учавствующих в определении ЭВзО снимков, для которых измерены x1,,y1,,p,q либо x1,y1,x2,y2.
n-5- число избыточных уравнений.
Задачу уравнивания решают по методу наименьших квадратов(МНК) под условием [PVV]=min
З
(1.24)
An5X51+Ln1=Vn1 ;
An5-матрица коэффициентов уравнений поправок:
 a1
b1
c1
d1
e1
a1
b1
c1
d1
e1
(1.25)
. . . . . . . . . . . .
. an bn cn dn en
Ln1- вектор свободных членов:
 l1
l1
(1.26)
Ln1= l2 ,
ln
X51- вектор неизвестных :
 δ1'
δ1'
X51
=
(1.27)
δ
δ
Vn1 – вектор невязок :

(1.28)
Vn1=
. . . .
Vn
П
(1.29)
B55X51+C51=0 ,
г
(1.30)
B55=A5nAn5 ;
C
(1.31)
C51=A51Ln1 .
В уравнение (1.29) входят 5 уравнений, число нормальных уравнений равно числу неизвестных.
(1.32)
X51=B55-1C51 ,

 δ1'
δ1'
X51=
(1.33)
δ
δ
Затем вычисляются исправленные значения ЭВзО в первой итерации:
 1'I
=
1'0
+ δ1'I
1'I
=
1'0
+ δ1'I
(1.34)
1’I = 1’0 + δ1’I .
I = 0 + δI
I = 0 + δI
Для того, чтобы перейти к другой итерации, нужно проверить условие:


 δ1'k
- δ1'
k-1
< ε
δ1'k
- δ1'
k-1
< ε
(1.35)


 δ1’k
- δ1’
k-1 <ε ,
δ1’k
- δ1’
k-1 <ε ,

 δk
- δk-1
<
ε
δk
- δk-1
<
ε

 δk
- δk-1
<
ε
δk
- δk-1
<
ε
где к и к-1 – номера последующей и предыдущей итерации ;
![]() -допустимая величина,
которая зависит от цели решаемой задачи,
если условие (1.35) не выполняется, то
вычисление ЭВзО производится в новой
итерации.
-допустимая величина,
которая зависит от цели решаемой задачи,
если условие (1.35) не выполняется, то
вычисление ЭВзО производится в новой
итерации.
Д
(1.36)
N=Nзаданное ,
где N-выполненное число итераций , а Nзаданное- заданное число итераций.
Апостериорная оценка точности определения ЭВзО выполняется по следующим величинам:
– проверяется точность выполнения условия компланарности соотвественных лучей, проверяется качество выполнения условия (1.5). Подставим в условие (1.5) вычисленные значения ЭВзО в последней итерации. Запишем условие (1.5) через трансформированные координаты точек левого и правого снимков:

(1.37)
.
X2’=x20 ; Y2’=y20; Z2’= -f
Подставим формулы (1.37) в уравнение (1.15) :
c
(1.38)
р
(1.39)
cos cos ( y10-y20) - cos sin p0 + sin( - x10y20/ f + y10x20)= 0 .
В формуле (1.39) x10,x20,y10,y20- трансформированные координаты соответсвенных точек левого и правого снимков, вычисленные через элементы взаимного ориентирования снимков, полученные в последней итерации. Они вычисляются по формулам:

x
10=-
f
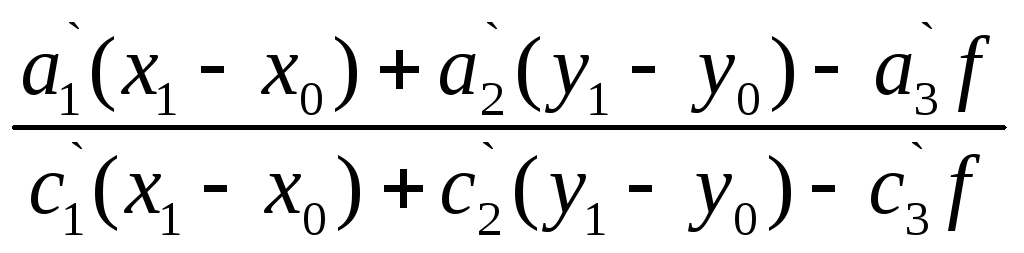
y10=
-f
 .
.
(1.40)
.![]()
y20=-f
![]()
Теоретически cos cos ( y10-y20) - cos sin p0 + sin( - x10y20/ f + y10x20/f)=0, однако практически cos cos ( y10-y20) - cos sin p0 + sin( - x10y20/ f + +y10x20/f)≠0, эта величина – остаточный поперечный параллакас.
Ф
(1.41)
δq= cos cos ( y10-y20) - cos sin p0 + sin( - x10y20/ f + y10x20/f).
Величина δq характеризует точность определения ЭВзО снимков:
Средне квадратическая ошибка δq:
(1.42) .
.
(1.43)
Средняя квадратическая ошибка единицы веса:
μ
=
 ,
,
где k- число неизвестных, в данном случае оно равно 5, тогда
(1.44) .
.
3. Средние квадратические ошибки ЭВзО снимков:
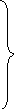
m1'
= μ![]()
(1.45)![]()
m2’
= μ![]() .
.
mυ
= μ![]()
mτ
= μ
![]()
На следующем этапе выполняется контроль качества результатов определения элементов взаимного ориентирования, для этого вычисленные величины δq,mσq,μ, m1', m1’. m2’, mυ, mτ сравнивают с допусками[Инструкция по фотограмметрическим работам при создание йифровых карт и планов. М.,2002,100с.], в качестве допустимой величины приведена mqдоп.=10 мкм = 0,01мм.Если допуски выполняются, то решение задачи взаимного ориентирования считается законченным. Если допуски не выполняются, то производится анализ результатов, с целью выявления ошибок, тогда либо измеряют δq заново, либо данная точка исключается из процесса взаимного ориентирования снимков, после чего элементы взаимного ориентирования вычисляются заново.
