2.6.2 Оценка точности способа полярных координат
Для способа полярных координат (рис.2.18) матрица параметрических уравнений поправок на основании формул (1.19) и (1.21) имеет следующий вид
(2.27) (2.28) (2.30) (2.31) (2.40)
Матрица весов результатов измерений имеет следующий вид
(2.41)
Следовательно матричное уравнение (1.18) в общем виде для способа полярных координат решения не имеет, поскольку на диагонали матрицы Р находится неизвестное соотношение СКО отложения углов и длин линий. Для устранения отмеченной неопределенности априорно зафиксируем неизвестное соотношение между СКО откладываемых элементов в виде произвольного положительного числа К. В этом случае принятое условие (1.23) и (1.24) имеет следующий вид
(2.42)
Исходя из этого условия, в способе полярных координат необходимая точность отложения угла может быть вычислена по формуле
(2.43)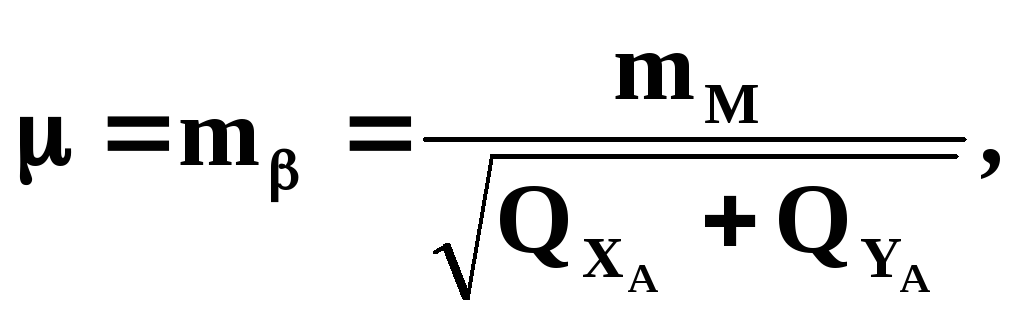
а необходимая точность отложения длин линий с использованием следующего выражения
(2.44)
Отметим, что размерность mL и mМ в формулах (2.43) и (2.44) должны совпадать. Структура матрицы весовых коэффициентов для способа полярных координат полностью соответствует структуре матрицы, полученной для прямой угловой засечки (2.35).
Для способа полярных координат матрица параметрических уравнений поправок в численном виде будет иметь следующий вид
В том случае, когда коэффициент К=1 решение матричного уравнения (1.18) приводит к матрице весовых коэффициентов следующего вида
Необходимая точность отложения углов и длин линий составит в соответствии с формулой (2.43) и (2.44) следующие численные значения
Следовательно, по результатам использования данного алгоритма, при отложении углов в способе полярных координат, типовая технология отложения углов должна соответствовать измерению углов в полигонометрии 4 класса mβ=3”.
Выполним оценку точности запроектированной фигуры разбивки, с использованием следующей, в данном варианте строгой формулы
(2.45)
Применяя к формуле (2.45) “принцип равного влияния” имеем
(2.46)
Расхождение между полученными результатами объясняется тем обстоятельством, что использование строгого алгоритма, основанного на вычислении обратной матрицы (1.18), в условиях, когда число измерений равно числу определяемых параметров (в фигуре разбивки отсутствуют избыточные измерения) приводит к неудовлетворительным результатам. Следовательно, для способа полярных координат рекомендуется использовать формулы (2.45 и 2.46) на основании которых типовая технология отложения углов должна соответствовать 2 разряду при построении ГСС /1/ с нормативной точностью угловых измерений mβ=10”.
2.6.3 Оценка точности линейной засечки
Для линейной засечки изображенной на рисунке 2.19 оценка точности выполняется по аналогии с прямой угловой засечкой и способом полярных координат. Матрица параметрических уравнений поправок А в формуле (1.18) на основании формул (1.21) будет выглядеть следующим образом
(2.47)
Если за СКО единицы веса принять СКО линейных измерений =mL, то матрица весов результатов линейных измерений на основании формулы
(2.48)
будет по аналогии с прямой угловой засечкой представлена в виде единичной матрицы следующего вида
(2.49)
Матрица весовых коэффициентов совпадает с матрицей весовых коэффициентов, полученной для способа прямой угловой засечки, а необходимую точность отложения длин линий можно вычислить по следующей формуле
(2.50)
В численном виде матрица параметрических уравнений поправок А для рассматриваемого варианта будет иметь следующее значение
В результате решения матричного уравнения (1.18) матрица весовых коэффициентов Q в численном виде будет иметь следующий вид
На основании формулы (2.50) необходимая точность линейных измерений может быть вычислена исходя из следующего выражения
Использование приближенной формулы для линейной засечки, состоящей из двух симметричных треугольников, приводит к следующим результатам
(2.51)
Отметим, что в данном случае погрешность использования приближенной формулы составляет примерно также 10%, как и в прямой угловой засечке.