
- •Лабораторная работа №1
- •3. Литература
- •4. Содержание и форма отчета
- •5. Контрольные вопросы
- •6. Методика выполнения лабораторной работы
- •Задание 1. Построить интервальный вариационный ряд распределения Краткие теоретические сведения
- •Решение
- •Задание 2. Построить гистограмму частот интервального вариационного ряда Краткие теоретические сведения
- •Задание 2. Построить гистограмму частот интервального вариационного ряда Решение
- •Краткие теоретические сведения
- •Задание 3. Записать эмпирическую функцию распределения и построить ее график Решение
- •Задание 4. Рассчитать основные числовые характеристики вариационного ряда Решение
- •4А) Мода – это варианта, имеющая наибольшую частоту.
- •Для определения остальных числовых характеристик воспользуемся методом произведений.
- •4Е)Асимметрия (коэффициент асимметрии)
- •Задание 5. Определение границ истинных значений числовых характеристик изучаемой случайной величины с заданной надёжностью Краткие теоретические сведения
- •Задание 5. Определение границ истинных значений числовых характеристик изучаемой случайной величины с заданной надёжностью Решение
- •Задание 6. Содержательная интерпретация результатов первичной обработки по условию задачи
- •7. Интерпретация значения коэффициента вариации V.
- •Задание 6. Содержательная интерпретация результатов первичной обработки по условию задачи Решение
- •3. Интерпретация среднего квадратичного отклонения .
Для определения остальных числовых характеристик воспользуемся методом произведений.
Введем условные варианты.
![]() ,
где С – «ложный нуль».
,
где С – «ложный нуль».
Чаще всего в качестве ложного нуля
принимается либо варианта, находящаяся
в середине вариационного ряда, либо
мода
![]() (варианта
(варианта![]() ,
имеющая наибольшую частоту), либо любое
другое число, упрощающее расчеты.
,
имеющая наибольшую частоту), либо любое
другое число, упрощающее расчеты.
Если за
![]() принять какое - либо значение
принять какое - либо значение![]() ,
то соответствующая ему условная варианта
,
то соответствующая ему условная варианта![]() будет равна нулю, а слева и справа от
нуля будут располагаться соответственно
значения
будет равна нулю, а слева и справа от
нуля будут располагаться соответственно
значения![]() 1,
1,![]() 2,
2,![]() 3,
3,![]() 4
и т.д.
4
и т.д.
ПримемС = 547,5,h= 5. Составим расчетную таблицу:
Таблица 4.
-
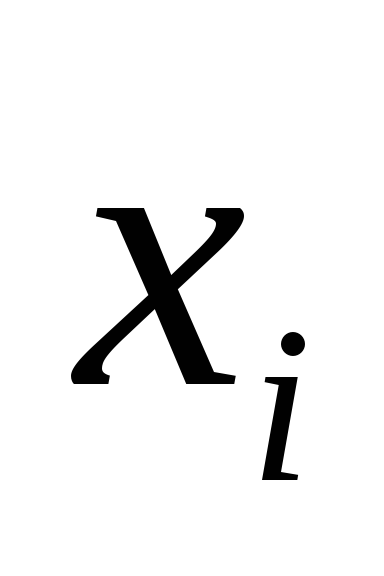
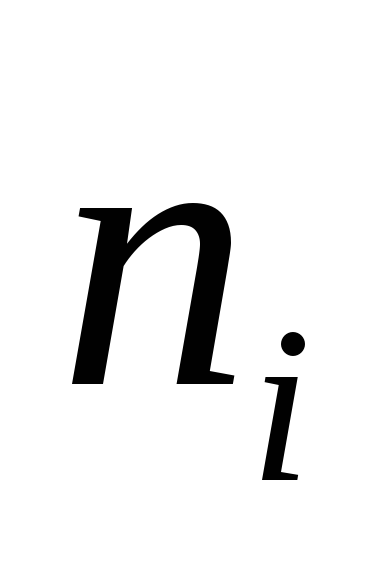
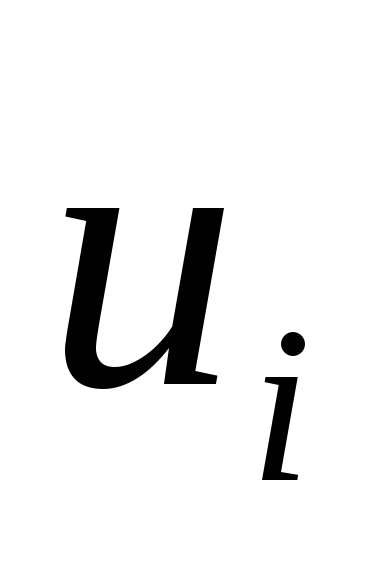
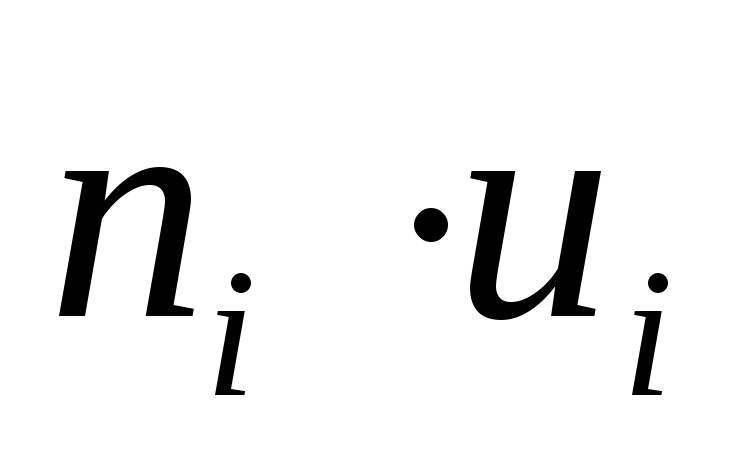
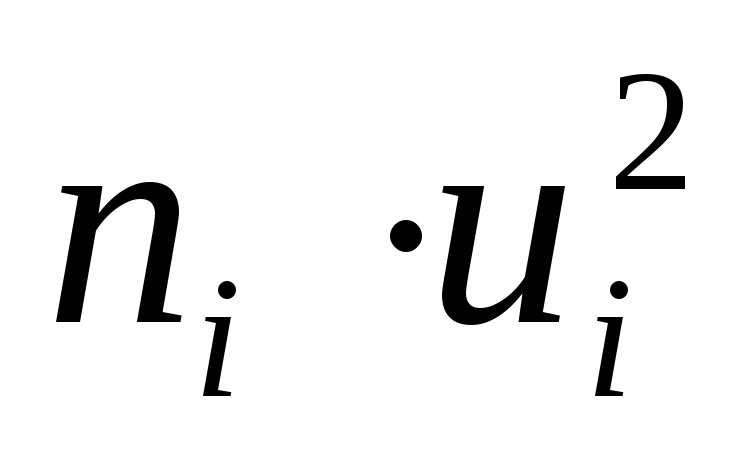
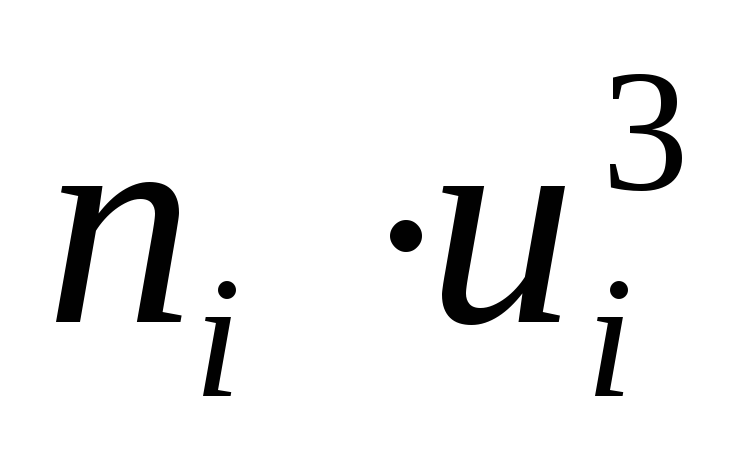
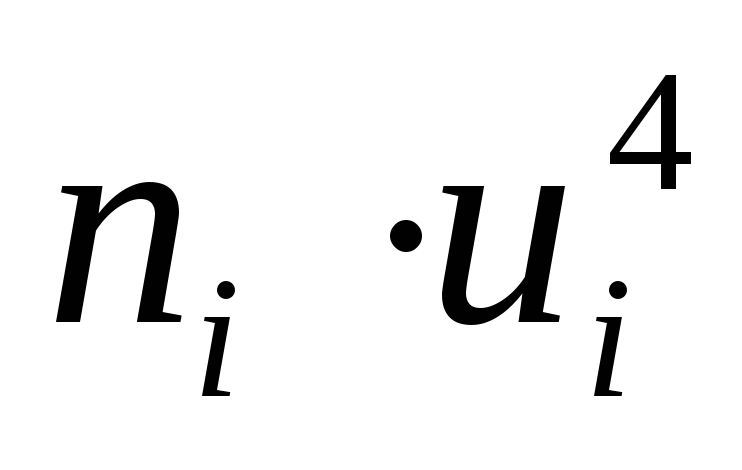
ni(ui +1)4
532,5
4
-3
-12
36
-108
324
64
537,5
10
-2
-20
40
-80
160
10
542,5
8
-1
-8
8
-8
8
0
547,5
26
0
0
0
0
0
26
552,5
17
1
17
17
17
17
272
557,5
23
2
46
92
184
368
1863
562,5
7
3
21
63
189
567
1792
567,7
5
4
20
80
320
1280
3125

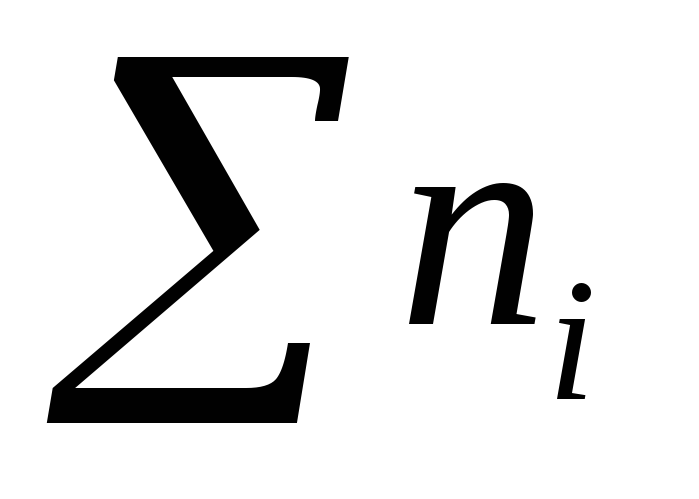 =
100
=
100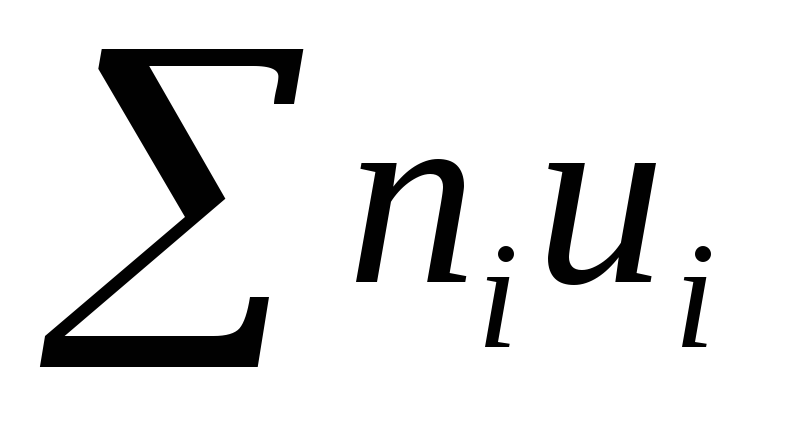 =
64
=
64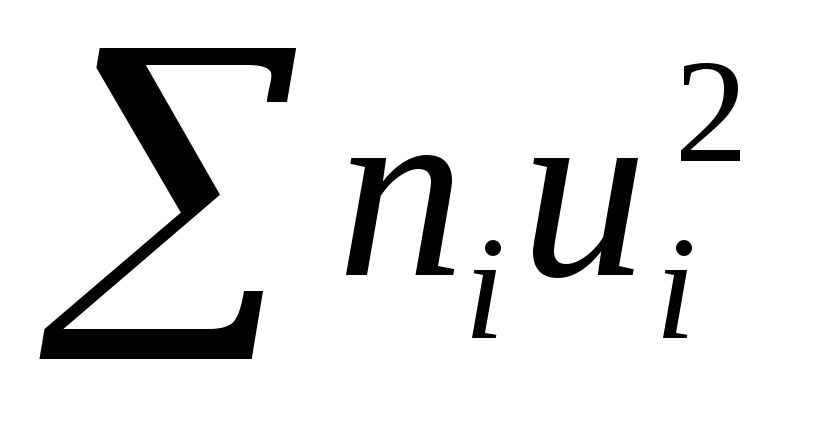 =
336
=
336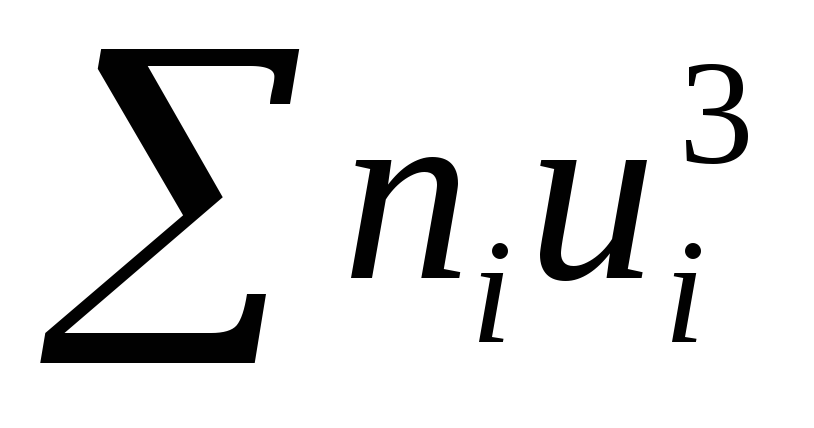 =
514
=
514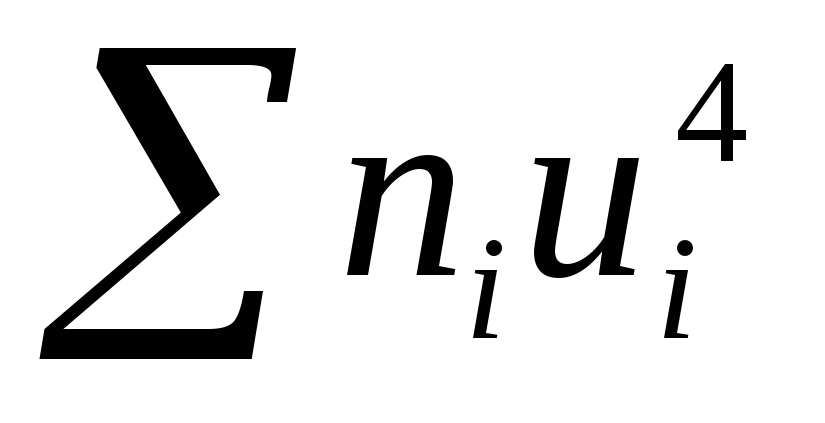 =
2724
=
2724∑= 7152
В![]() ыполним
проверку.
ыполним
проверку.
2724+4*(514)+6*336+4*(64)+100=7152
4б)Условные начальные моментынайдем по формулам:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
4в)Выборочная средняя
![]()
![]() =
550,7
=
550,7
4г)Дисперсия(рассеивание) – характеристика рассеяния значений случайной величины Х около ее математического ожидания.
Выборочная дисперсия
![]()
![]() =
=
![]() ≈ 73,8
≈ 73,8
Среднее квадратичное отклонениетакже служит для оценки рассеяния
случайной величины Х вокруг ее среднего
значения
![]()
![]() ≈
8,6
≈
8,6
Исправленная дисперсия генеральной совокупности
![]() =
100/99*73,8 ≈ 74,54
=
100/99*73,8 ≈ 74,54
Исправленное среднее квадратичное
отклонение![]() ≈
8,63
≈
8,63
4д)Коэффициентом вариацииV
![]() ;
;
![]()
4Е)Асимметрия (коэффициент асимметрии)
Для вычисления асимметрии и эксцесса найдем центральные моменты:
![]()
![]() ≈
- 98,36
≈
- 98,36
![]()
![]() ≈ -292,24
≈ -292,24
Асимметрия
![]()
![]() ≈
-0,15
≈
-0,15
4и)Эксцессвычисляем по формуле:
![]() ;
;
![]()
Задание 5. Определение границ истинных значений числовых характеристик изучаемой случайной величины с заданной надёжностью Краткие теоретические сведения
Доверительные интервалы находят для
оценки неизвестного математического
ожидания α нормального распределения
по выборочной средней
![]() при неизвестном(или при известном)
генеральной совокупности.
при неизвестном(или при известном)
генеральной совокупности.
Доверительный интервал – это интервал, который покрывает неизвестный параметр α с заданной надежностьюγ.
Известно, что истинное значение измеряемой величины равно ее математическому ожиданию α. Поэтому задача сводится 1) к оценке математического ожиданияα при неизвестном, т.к. в задании на лабораторную работу не дано значениегенеральной совокупности; 2) к оценке среднего квадратичного отклонения нормального распределения.
5а)Доверительный интервал для оценки
математического ожидания нормального
распределения при неизвестном среднем
квадратичном отклонении генеральной
совокупности, покрывающий математическое
ожидание с заданной надежностью, имеет
вид:![]() ,
гдеs– исправленное
среднее квадратичное отклонение;
,
гдеs– исправленное
среднее квадратичное отклонение;![]() -
табличное значение, которое зависит от
заданной надежностиγ и объема
выборки см. «Таблицу значений
-
табличное значение, которое зависит от
заданной надежностиγ и объема
выборки см. «Таблицу значений![]() »
Приложение 3 учебника.
»
Приложение 3 учебника.
5б)Доверительный интервал для оценки среднего квадратичного отклонения нормального распределения, покрывающийс заданной надежностью имеет вид:
![]() ,
гдеs– исправленное
среднее квадратичное отклонение;
,
гдеs– исправленное
среднее квадратичное отклонение;![]() -
табличное значение находится по «Таблице
значений
-
табличное значение находится по «Таблице
значений![]() »
(см. Приложение 4 учебника)
»
(см. Приложение 4 учебника)
