6.5.Центр тяжести

При рассмотрении материальных тел, размерами которых можно пренебречь по сравнению с радиусом Земли, силы тяжести частей, составляющих тело, можно приближенно считать системой параллельных сил. Центром тяжести твердого тела называют неизменно связанную с этим телом точку С, через которую проходит линия действия равнодействующей сил тяжести частиц данного тела при любых его положениях в пространстве.

Ограничимся рассмотрением методов определения центров тяжести плоских фигур. Для однородного тела, имеющего форму тонкой пластины постоянной толщины, существуют следующие формулы для определения координат ее центра тяжести:

(1)

где

(2)

- осевые статические моменты плоской фигуры относительно осей xиy, лежащих в ее плоскости;- площадь фигуры,A_k,x_k,y_k- площади и координаты центров тяжести частей, составляющих фигуру.

Основным свойством статического момента является то, что он равен нулю относительно осей, проходящих через центр тяжести фигуры. Отсюда, в частности, следует, что если однородное тело имеет плоскость, ось или центр симметрии, то его центр тяжести лежит, соответственно, в этой плоскости, на этой оси или в этом центре.

Метод разбиения тела на части и метод отрицательных масс непосредственно определен формулами (1), (2). Разбиение фигуры производится на части, положения центров тяжести и площади которых могут быть легко определены. Метод отрицательных масс предполагает присвоение отрицательного знака площадям вырезов при рассмотрении многосвязных фигур.

Примеры определения центра тяжести плоской фигуры

П-1

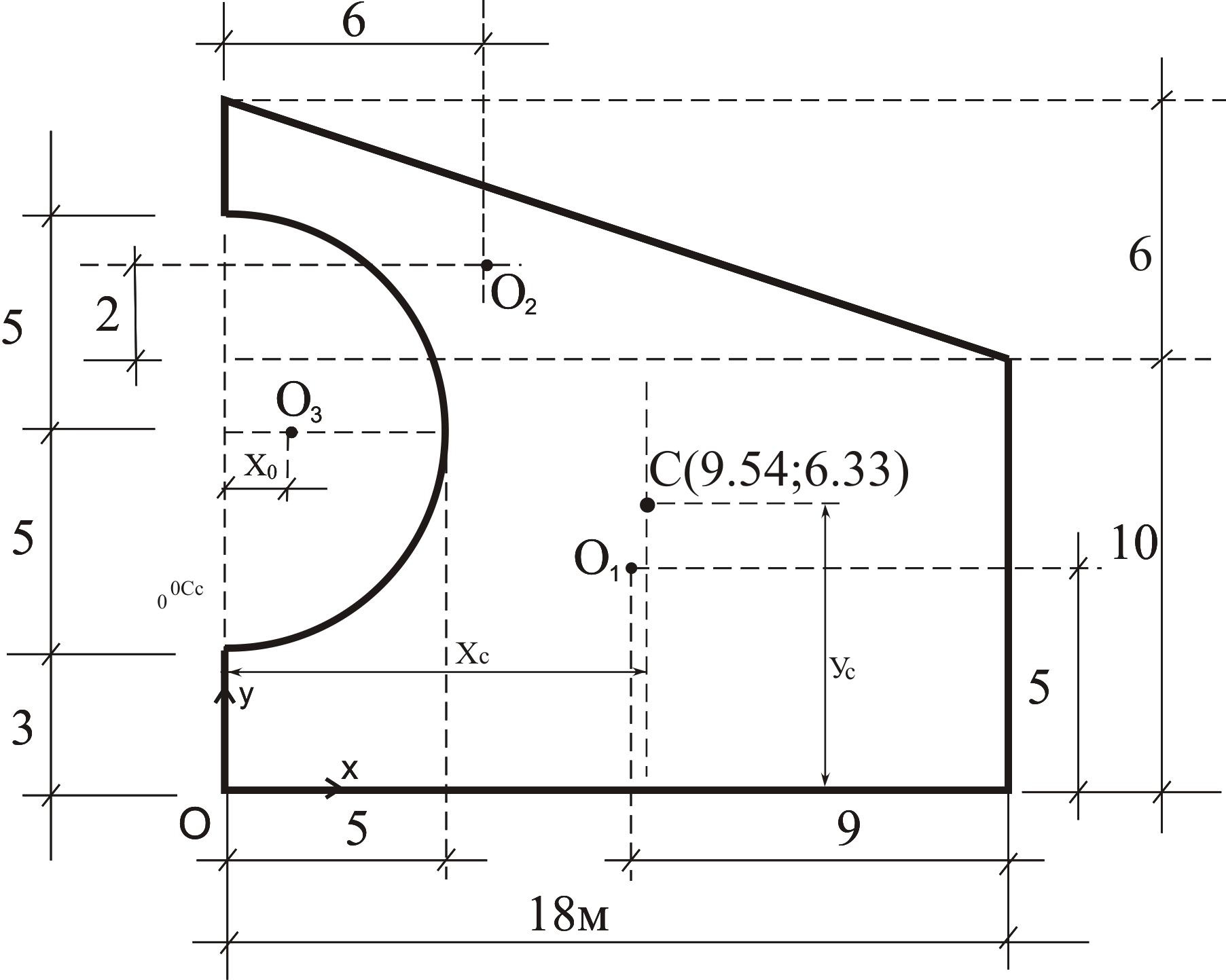
Разбиваем фигуру на составные части: 1-я – прямоугольник (18х10),

2-я – треугольник (18х6) и 3-я – полукруг, ограниченный дугой окружности радиуса r=5м. Отмечаем центры тяжести каждой из частейи «привязываем» их местонахождения к декартовой ортогональной систем системе координатxOy.

x₀– расстояние от центра тяжести полукруга О₃до центра тяжести круга.

Положение центра тяжести фигуры определим относительно точки О – начала координат

,

в которых – площадь фигуры, А_i– площади составляющих ее частей,

– осевые статические моменты фигуры.

х_i,y_i– координаты центров тяжести составляющих фигуру частей.

Для упорядочивания расчетов составим таблицу:

№ части	хi	уi	Ai	хi Ai	уiAi
1	9	5	90	810	450
2	6	12	54	324	648
3	2.12	8	-39.3	-83.3	-314
			А=	Sy=	Sx=

Окончательно получим:

Точку С(х_с , у_с) в принятом масштабе отмечаем на фигуре.

П-2 определения положения центра тяжести плоской фигуры

Разбиваем данную фигуру на составляющие ее части: прямоугольник abek, треугольникkedи полукругmnk. Фиксируем на рисунке положения их центров тяжести (т.т. О₁, О₂, О₃). При этом расстояние от центра круга до центра тяжести полукруга вычисляем по формуле

Положение центра тяжести фигуры определим относительно произвольно выбранной системы координат xKyс помощью формул

.

Обозначим через - координаты центров тяжести и площади составляющих фигуру частей, составим таблицу

Номер части	xi (дм)	yi (дм)	Ai (дм2)	xiAi (дм3)	yiAi (дм3)
1	-5	6	120	-600	720
2	-4	1.7	-25.13	100.5	-42.72
3	2	8	36	72	288

Так как

окончательно получим

Положение центра тяжести отмечено чертеже фигуры.

Критерии оценки (в % от 100) (штрафные санкции)

Пропуск 2-х занятий ( -5). Решение лишь одной задачи контрольной работы (-60) . Решение лишь двух задач (-30) Решение всех 3-х задач (0). Некачествен-ное оформление работы (-5). Без ответа на два из пяти вопросов по теории (-5).

Пропуск 2-х занятий ( -5). Решение лишь одной задачи контрольной работы (-60) . Решение лишь двух задач (-30) . Решение всех задач (0). Некачественное оформление работы (-5). Без ответа на два из пяти вопросов по теории (-5). Тест 1: правильных ответов 90-100% – (0) 80-89% – (-5) 60-79% –(-15) 50-59% – (-20)0-49% (-30).

Пропуск 2-х занятий ( -5). Неверно определены реакции опор фермы (-50) . Определены: 3 из 6 усилий (-30) , 4 из 6 усилий (-20) , 5 из 6 усилий (-10) , 6 из 6 усилий (0) , Некачественное оформление работы (-5), Без ответа на два из пяти вопросов по теории (-5).

Пропуск 2-х занятий ( -5). Ход решения задачи контрольной работы верен, ошибки в счете (-30) . Решение задачи полностью верно (0) . Некачественное оформление работы (-5). Без ответа на два из пяти вопросов по теории (-5). Тест 2: правильных ответов 90-100% – (0) 80-89% – (-5) 60-79% –(-15) 50-59% – (-20) 0-49% –(-30)

35