
9_физ_2(кинематика)
.pdf
Министерство образования и науки Российской Федерации Московский физико-технический институт
(государственный университет) Заочная физико-техническая школа
ФИЗИКА
Кинематика
Задание №2 для 9-х классов
(2015 – 2016 учебный год)
г. Долгопрудный, 2015

2015-2016 уч. год, №2, 9 кл. Физика. Кинематика
Составитель: В.И. Чивилёв, доцент кафедры общей физики МФТИ. Е.В. Паркевич, бакалавр МФТИ.
Физика: задание №2 для 9-х классов (2015 – 2016 учебный год), 2015, 28 с.
Дата отправления заданий по физике и математике – 29 октября 2015 г.
Учащийся должен стараться выполнять все задачи и контрольные вопросы в заданиях. Некоторая часть теоретического материала, а также часть задач и контрольных вопросов, являются сложными и потребуют от учащегося больше усилий при изучении и решении. В целях повышения эффективности работы с материалом они обозначены символом «*» (звёздочка). Мы рекомендуем приступать к этим задачам и контрольным вопросам в последнюю очередь, разобравшись вначале с более простыми.
Составители:
Чивилёв Виктор Иванович Паркевич Егор Вадимович
Подписано 04.06.15. Формат 60×90 1/16. Бумага типографская. Печать офсетная. Усл. печ. л. 1,75.
Уч.-изд. л. 1,55. Тираж 1200. Заказ №3-з.
Заочная физико-техническая школа Московского физико-технического института (государственного университета)
ООО «Печатный салон ШАНС»
Институтский пер., 9, г. Долгопрудный, Московская обл., 141700. ЗФТШ, тел./факс (495) 408-51-45 – заочное отделение,
тел./факс (498) 744-63-51 – очно-заочное отделение, тел. (498) 755-55-80 – очное отделение.
e-mail: zftsh@mail.mipt.ru
Наш сайт: www.school.mipt.ru
© МФТИ, ЗФТШ, 2015
Все права защищены. Воспроизведение учебно-методических материалов и материалов сайта ЗФТШ в любом виде, полностью или частично, допускается только с письменного разрешения правообладателей.
2015, ЗФТШ МФТИ, Чивилёв Виктор Иванович Паркевич Егор Вадимович
2

2015-2016 уч. год, №2, 9 кл. Физика. Кинематика
1. Задача механики
Все мы хорошо знаем, что любое физическое явление или процесс в окружающем нас материальном мире представляет собой закономерный ряд изменений, происходящих во времени и пространстве. Механическое движение, под которым мы понимаем изменение положения данного тела (или его частей) относительно других тел, и есть простейший вид физического процесса. Механическое движение тела представляет собой достаточно сложную и интересную науку, а соответствующий раздел физики, изучающий её, называется механикой. Основная задача механики заключается в том, чтобы определить положение тела в любой момент времени. Стоит отметить, что сама механика делится на множество разных частей, каждая из которых занимается определённой задачей. Одной из таких является кинематика. Именно эту часть механики мы и рассмотрим в данной работе.
2. Что же такое кинематика?
Кинематика отвечает на вопрос: как движется тело, не вдаваясь при этом в подробности причин, вызывающих это движение. Далее, когда мы говорим о движении некоторого тела, то мы подразумеваем изменение его положения в пространстве и времени. Но чтобы определить его положение в любой момент времени, необходимо выбрать соответствующее тело отсчета, относительно которого будет рассматриваться движение интересующего нас тела, при этом с телом отсчёта жёстко связывают систему координат (например, декартову). Всё вместе это задаёт систему отсчёта, под которой понимают систему координат (жёстко связанную с телом отсчёта) и "часы"– любой прибор отсчитывающий время.
3. Упрощение в виде материальной точки
Стоит отметить, что описание движения тела – очень сложная задача. Поэтому физики для ответа на какой-либо вопрос часто прибегают к упрощениям. В качестве примера рассмотрим следующее упрощение. Ясно, что всякое тело имеет определенные размеры. Различные части тела находятся в разных местах пространства. Однако, во многих задачах механики нет необходимости указывать положения отдельных частей тела, если его размеры малы по сравнению с расстояниями до других тел. Тогда тело можно считать материальной точкой. То есть реальный объект заменяется точечным с той же массой, поэтому когда в задаче говорится о движении материальной точки, надо помнить, что она ещё наделена массой. Так можно поступать, например, при изучении движения планет вокруг Солнца.
2015, ЗФТШ МФТИ, Чивилёв Виктор Иванович Паркевич Егор Вадимович
3
2015-2016 уч. год, №2, 9 кл. Физика. Кинематика |
|
|
|
|
|
|
|
|
|||||||
Наряду с материальной точкой, в механике ещё одним ключевым |
|||||||||||||||
понятием служит приближение в виде абсолютно твёрдого тела. В |
|||||||||||||||
данном случае реальный объект рассматривается в качестве системы |
|||||||||||||||
материальных точек, расстояния между которыми в условии задачи |
|||||||||||||||
можно считать неизменными. |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
4. Путь и перемещение |
|
|
|
|
|
|
|
||||
Положение материальной точки в пространстве в любой момент |
|||||||||||||||
времени (закон движения) можно определять либо с помощью |
|||||||||||||||
зависимости |
координат |
от |
времени |
x = x(t), y = y(t), z = z(t) |
|||||||||||
(координатный способ), либо при помощи зависимости от времени |
|||||||||||||||
радиус-вектора r (t) (векторный способ), проведенного из начала |
|||||||||||||||
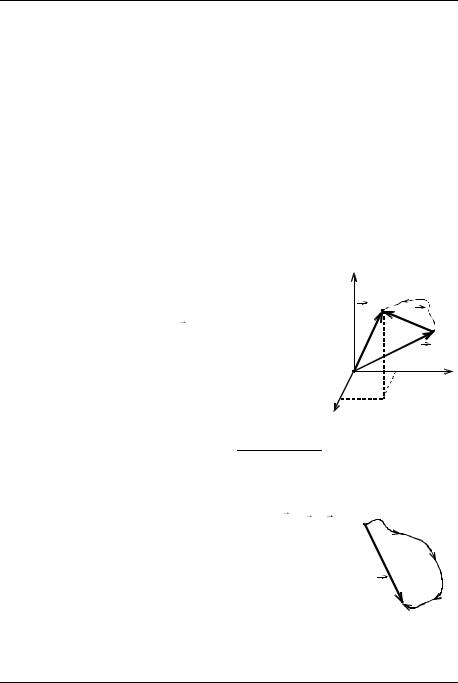
координат до данной точки (см. рис.1). Начальное положение тела |
(в |
||||||||||||||
момент времени t0 = 0 ) задаётся начальным радиусом-вектором |
r0 , |
||||||||||||||
координаты которого (x0 ; y0 ; z0 ) . |
|
|
|
|
z |
|
|
|
|
||||||
Комментарий к рис. 1. Определение положения |
|
|
B |
|
L |
|
|||||||||
точки с помощью координат |
x = x(t), y = y(t) |
и |
|
r(t) |
r |
|
|||||||||
|
|
|
|
|
|
r0 |
|
|
|
|
|
|
|||
z = z(t) |
и радиус-вектора |
r ; |
– радиус-вектор |
|
|
|
|
A |
|||||||
положения точки в начальный момент времени. |
|
|
|
|
|
r0 |
|
||||||||
Линия, по которой движется некоторая точка |
|
O |
|
|
|
|
|||||||||
тела, называется траекторией движения этой |
|
|
|
|
y |
||||||||||
|
|
|
|
|
|||||||||||
точки. Данную |
траекторию легко описать, |
если |
|
x |
|
|
|
|
|||||||
известны зависимости координат точки от |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
||||||||||
времени. Длина участка траектории, пройденного |
|
Рис. 1 |
|
||||||||||||
точкой при ее движении, называется пройденным |
|
|
|
|
|
|
|||||||||
путём |
L, |
а вектор, |
соединяющий начальную |
и |
конечную |
точки |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
траектории, называется перемещением S . |
Из |
рис. 1 видно, что |
|||||||||||||
перемещение тела из точки |
A в точку B равно изменению радиус- |
||||||||||||||
векторов, соединяющих данные точки, т. е. S = r r0 . |
a |
|
|
L |
|
||||||||||
В случае достаточно малого промежутка времени t |
|
|
|
|
|||||||||||
|
|
|
|
|
|||||||||||
пройденный телом путь L почти совпадает |
с |
|
|
|
|
|
|||||||||
модулем вектора перемещения. Однако нельзя путать |
|
S |
|
|
|
||||||||||
их! Дело в том, что при движении тела по |
|
|
|
|
|||||||||||
|
|
|
|
|
|||||||||||
криволинейной |
траектории |
модуль |
вектора |
|
|
b |
|
|
|||||||
перемещения |
всегда |
меньше |
пройденного |
пути |
|
Рис. 2 |
|
||||||||
(рис. 2). |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Комментарий к рис. 2. пройденный путь |
L |
и |
|
|
|
|
|
||||||||
2015, ЗФТШ МФТИ, Чивилёв Виктор Иванович |
|
|
|
|
|
|
|
|
|||||||
|
|
|
Паркевич Егор Вадимович |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |

2015-2016 уч. год, №2, 9 кл. Физика. Кинематика
вектор перемещения S при криволинейном движении тела; a и b – начальная и конечная точки пути.
Как мы уже сказали выше, процесс движения тела может быть очень сложным. Например, тело может вращаться вокруг какой-нибудь оси, либо двигаться поступательно. Наиболее простым в этом случае является последний тип движения. В этом случае все точки тела перемещаются одинаково, и для описания движения всего тела достаточно выяснить зависимость координат от времени для произвольно выбранной точки тела.
5.Понятие скорости движения.
5.1.Приращения и их геометрический смысл
Для количественной характеристики процесса движения тела вводится понятие скорости движения, но прежде, чем мы дадим её определение, рассмотрим некоторые вспомогательные понятия из математики для более ясного подхода.
Пусть x – произвольная точка, лежащая в некоторой окрестности
фиксированной точки x0 . Разность |
x x0 называется |
приращением |
независимой переменной (или приращением аргумента) |
в точке x0 и |
|
обозначается x . Таким образом, |
x = x x0 , откуда |
следует, что |
x = x0 x . Говорят также, что первоначальное значение аргумента
x0 получило приращение x . Вследствие этого значение функции |
f |
|
изменится на величину: |
|
|
f = f (x) f (x0 ) = f (x x) f (x0 ) |
(1) |
|
Эта разность называется приращением функции |
f в точке |
x0 , |
соответствующим приращению x , и обозначается символом f . |
Из |
|
этого выражения видно, что при фиксированном x0 |
приращение |
f |
есть функция от x . f называют также приращением зависимой переменной и обозначают через y для функции y = f (x). Рассмотрим
следующий пример.
Пример №1. Найдите приращение f функции x0 , если приращение аргумента равно x .
Решение: Согласно (1) будем иметь:
f = f (x x) f (x ) = |
|
1 |
|
1 |
= |
x0 (x0 x) |
|
|
|
|
|||
0 |
x0 |
x |
|
x x0 (x0 x) |
||
|
|
|||||
f (x) = 1/x в точке
= |
|
x |
. (2) |
|
|
|
|||
x (x |
x) |
|||
0 |
0 |
|
|
|
2015, ЗФТШ МФТИ, Чивилёв Виктор Иванович Паркевич Егор Вадимович
5
2015-2016 уч. год, №2, 9 кл. Физика. Кинематика |
|
|
|
|
|
||||
|
x |
|
|
y |
|
|
C |
|
B |
Ответ: f = x (x x) . |
|
f(x + x) |
|
|
|
|
|||
|
|
|
|
|
|
||||
0 |
0 |
|
|
0 |
|
|
|
|
|
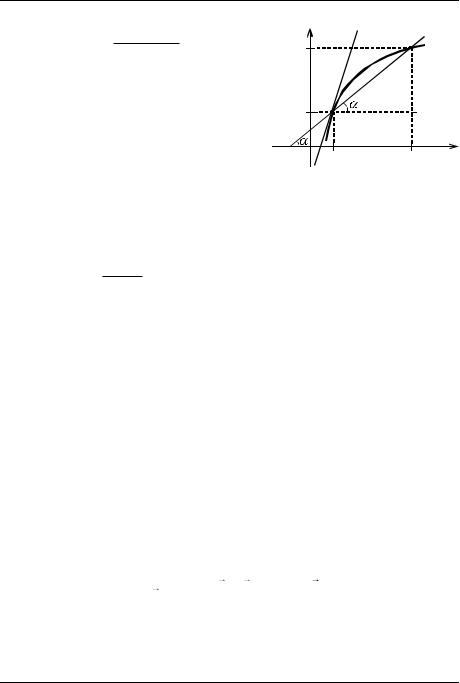
Зададимся теперь вопросом: в чём |
f |
|
|
l |
|
f |
|||
же состоит рис. 3 геометрический |
|
|
|
||||||
|
|
|
|
|
|
||||
смысл приращений |
f |
и |
x ? Для |
f (x0) |
A |
|
x |
|
|
этого на рис. 3 рассмотрим прямую l , |
|
|
|
|
|||||
|
|
|
|
|
|
||||
проходящую через любые две точки |
O |
x |
|
x |
|
x + x x |
|||
|
|
|
|
0 |
|
||||
графика функции |
f . Такую прямую |
|
|
|
|
0 |
|||
|
|
|
|
|
|
||||
ещё называют секущей к графику f . |
|
|
Рис. 3 |
|
|
||||
Комментарий к рис. 3. График |
|
|
|
|
|
|
|||
функции f (x) , пересекаемый прямой l |
в точках A и B . |
|
|
||||||
Угловой коэффициент k |
секущей, проходящей через точки (x0 ; y0 ) |
||||||||
и (x; y) , равен y y0 . Выразим его через приращения x и y |
|||||||||
x x |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
(рис. 3): |
|
|
|
|
|
|
|
|
|
|
|
|
k = tg = |
y |
|
|
|
|
(3) |
|
|
|
|
x |
|
|
|
|
|
Здесь мы воспользовались тем, что угловой коэффициент прямой |
|||||||||
y = kx b равен тангенсу |
угла наклона , |
который |
эта |
прямая |
|||||
образует с осью абсцисс. |
|
|
|
|
|
|
|
|
|
5.2.Средняя скорость
Спомощью введённых приращений удобно выражать среднюю скорость движения за промежуток времени [t0 ;t0 t]. Если точка
движется по прямой и известна её координата x(t) , то:
vср |
( t) = |
x |
= |
x(t0 |
t) x(t0 ) |
(4) |
t |
|
t |
||||
Поскольку в этом случае приращение |
x есть длина пути, который |
|||||
прошла точка за время t , то такую скорость ещё называют средней путевой.
Можно также ввести и среднюю скорость перемещения:
vср ( t) = |
r |
= |
r (t0 |
t) r (t0 ) |
(5) |
t |
|
t |
|||
|
|
|
|
Чтобы понять разницу между двумя этими понятиями рассмотрим следующий пример.
Пример №2 Известно, что автомобиль выехал из пункта A в пункт
2015, ЗФТШ МФТИ, Чивилёв Виктор Иванович Паркевич Егор Вадимович
6

2015-2016 уч. год, №2, 9 кл. Физика. Кинематика
B, расстояние между которыми LAB = 5 км. Время которое он затратил
на поездку равно = 5 мин. Затем автомобиль возвратился назад в пункт A . Найдите среднюю путевую скорость и среднюю скорость перемещения.
Решение: Поскольку начальное и конечное положения автомобиля
совпадают, то перемещение в этом случае равно нулю, т. е. |
r = 0. |
|||||||||||||||
Следовательно, и средняя скорость перемещения |
v |
|
= |
| r | |
|
= 0. |
Зато, |
|||||||||
ср |
|
t |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
как видим, средняя путевая скорость равна: |
|
|
|
|
|
|
|
|
|
|
||||||
|
v = |
L |
|
= |
5км |
= 1км / мин. |
|
|
|
|
|
|
|
|
|
(6) |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
ср |
|
|
5мин |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Ответ: |
средняя скорость |
перемещения v |
= |
| r | |
= 0, |
|
средняя |
|||||||||
|
|
|
||||||||||||||
|
|
|
|
|
|
ср |
|
|
t |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
путевая vср |
= 1 км/мин. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5.3. Понятие производной |
|
|
|
|
|
|
|
|
|
|
|||||
Введём теперь понятие производной функции |
f |
в точке |
x0 . В |
|||||||||||||
|
||||||||||||||||
математике вводится следующее определение: производной функции
f в точке x0 |
называется число, |
к которому стремится разностное |
|||||||
отношение: |
|
|
|
|
|
|
|
|
|
|
f = |
f (x0 |
x) f (x0 ) |
, при |
x 0 |
(7) |
|||
|
|
|
|
|
|||||
|
x |
x |
|
|
|||||
В случае функции y = f (x) |
производную обозначают следующим |
||||||||
образом: |
|
|
|
|
|
|
|
|
|
|
|
lim |
f |
= |
dy |
= y |
|
(8) |
|
|
|
x |
|
|
|||||
|
|
x 0 |
|
dx |
|
|
|||
Вернёмся к рис. 3. Если зафиксировать точку |
A и двигать по |
||||||||
направлению к ней точку B , |
то |
x неограниченно уменьшается и |
|||||||
приближается к |
0, а секущая |
ÀÂ приближается к касательной |
ÀÑ. |
||||||
Следовательно, предел разностного отношения равен угловому коэффициенту касательной в точке A. Отсюда следует: производная функции в точке есть угловой коэффициент касательной к графику этой функции в этой точке. В этом и состоит геометрический смысл производной.
5.4. Мгновенная скорость
Мгновенной скоростью v(t) поступательного движени материальной точки в момент времени t называется предел отношения малого
2015, ЗФТШ МФТИ, Чивилёв Виктор Иванович Паркевич Егор Вадимович
7

2015-2016 уч. год, №2, 9 кл. Физика. Кинематика
|
|
|
|
|
перемещения S к малому |
промежутку времени t, за который |
|||
произошло это перемещение, при условии t 0 : |
|
|||
v(t) = lim |
S |
, или v (t) = lim |
r . |
(9) |
t 0 |
t |
t 0 |
t |
|
Такой предел называется производной перемещения по времени. При этом проекция скорости на ось прямоугольной декартовой системы координат равна производной координаты по времени. Например, для проекции вектора скорости на ось X , получим:
|
|
x |
|
dx |
|
|
(10) |
|||||
|
vx (t) = lim |
= |
dt |
= x . |
||||||||
|
|
t 0 t |
|
|
|
|
|
|
|
|
||
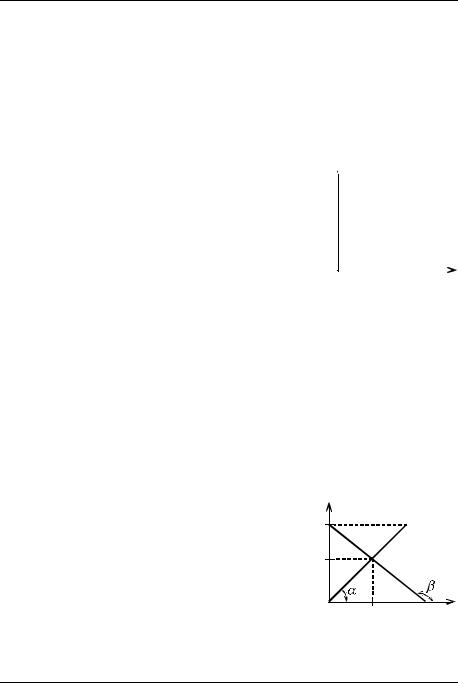
При последовательном уменьшении длитель- |
|
|
|
|
|
|||||||
v |
||||||||||||
ности промежутка времени t |
направление век- |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
тора перемещения |
S приближается к касатель- |
A |
||||||||||
ной в точке А |
траектории |
движения, |
через |
|
|
|
|
|
||||
которую проходит материальная точка в момент |
|
|
|
|
|
|||||||
|
S |
|||||||||||
времени t (см. |
рис. 4). Поэтому |
вектор |
v |
|
||||||||
|
|
|
|
|
||||||||
скорости лежит на касательной к |
траектории |
Рис. 4 |
||||||||||
движения материальной точки |
в точке |
À |
и |
|
|
|
|
|
||||
направлен в сторону движения материальной точки.
Комментарий к рис. 4. Вектор скорости v тела направлен по касательной к траектории движения в точке A.
Физический смысл выбора направления вектора скорости тела по касательной к траектории движения заключается в следующем. Как показывает опыт, при таком выборе вектор скорости указывает направление, в котором будет двигаться материальная точка из точки А траектории, если в момент прохождения этой точки действие любых других тел на нее прекратится.
Пример №3. Пусть при движении тела вдоль оси X его координата изменяется согласно уравнению x(t) = kt2 , где k = 5 м/с 2 . Найти мгновенную скорость v( ) в момент времени = 1 сек.
Решение: Чтобы определить значение мгновенной скорости в этот момент времени, необходимо сначала найти предел отношения x/ t при t 0. Воспользуемся здесь введёнными выше приращениями.
Пусть в момент времени t координата тела равна x1 = kt2 , а в момент
времени t t, соответственно, |
x = k(t t)2 |
. Следовательно, прира- |
|||
|
|
|
2 |
|
|
щение координаты равно: |
|
|
|
|
|
x = x |
x |
= k(t t)2 kt2 = 2kt t k( t)2. |
(11) |
||
2 |
1 |
|
|
|
|
Таким образом, искомое отношение равно:
2015, ЗФТШ МФТИ, Чивилёв Виктор Иванович Паркевич Егор Вадимович
8
2015-2016 уч. год, №2, 9 кл. Физика. Кинематика
|
x |
= 2kt k t. |
|
(12) |
|
|
|
|
|||
|
t |
|
|
||
Наконец, устремляя t 0 , получим, что: |
|
||||
v( ) = lim |
x = 2 5м / с2 |
1сек = 10м / с. |
(13) |
||
t 0 |
t |
|
|
||
Ответ: v( ) = 10 м/с. |
|
|
|
|
|
6.Равномерное и неравномерное движение
Взависимости от скорости движения выделяют два случая, а именно случай равно- v
 мерного движения и неравномерного. Движение
мерного движения и неравномерного. Движение
с постоянной по модулю и направлению A |
|
B |
||
|
||||
скоростью называется равномерным прямоли- |
|
L=v.t |
|
|
нейным движением. При равномерном прямо- |
|
|
||
линейном движении тело движется по прямой и |
|
|
|
|
за любые равные промежутки времени проходит |
O |
|
|
|
C t |
||||
одинаковые пути. При равномерном движении |
||||
|
|
|
||
график зависимости модуля скорости v от вре- |
|
Рис. 5 |
||
мени t является прямой, параллельной оси |
|
|
|
|
абсцисс (рис. 5).
Комментарий к рис. 5. График зависимости модуля скорости v от времени t . Путь L , пройденный телом за время t при равномерном движении
со скоростью v, определяется уравнением:
|
|
|
|
|
|
|
L = vt. |
|
|
|
(14) |
||
Если площадь |
прямоугольника |
ОАВС |
на |
графике |
зависимости |
||||||||
скорости v от времени t |
выразить в единицах произведения скорости |
||||||||||||
v на время t , то она соответственно будет равна пройденному пути L : |
|||||||||||||
|
|
|
|
|
|
OA ОС = vt. |
|
|
|
(15) |
|||
Рассмотрим следующий пример. |
|
|
|
|
|
|
|||||||
Пример |
№4. |
Пусть |
из |
пунктов |
A |
и |
x |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B, расстояние |
между |
которыми |
равно |
L , |
l |
|
|
||||||
одновременно |
навстречу |
друг |
другу |
начали |
|
|
|||||||
|
C |
|
|||||||||||
двигаться |
два |
автомобиля: |
первый |
со |
xC |
|
|||||||
|
|
||||||||||||
скоростью v1, второй v2 . Определите, через |
|
|
|||||||||||
|
|
|
|||||||||||
сколько времени они встретятся и расстояние |
|
|
|
||||||||||
от точки |
A |
до |
места их встречи. Решить |
O |
tC |
t |
|||||||
задачу графически. |
|
|
|
|
|
|
|
Рис. 6 |
|
||||
Решение. Зависимость координат авто- |
|
||||||||||||
|
|
|
|||||||||||
мобилей (рис. 6). Будем считать,что автомо- |
|
|
|
||||||||||
2015, ЗФТШ МФТИ, Чивилёв Виктор Иванович |
|
|
|
||||||||||
|
|
|
Паркевич Егор Вадимович |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |

2015-2016 уч. год, №2, 9 кл. Физика. Кинематика
били движутся равномерно и прямолинейно. В этом случае зависимость координат последних от времени будет иметь вид:
x1 = v1t, и x2 = l v2t. |
(16) |
В момент встречи координаты двух автомобилей будут равны, т. е. x1 = x2. Отсюда находим время t = L / (v1 v2 ), через которое эта
встреча произойдёт, а также расстояние lv1 / (v1 v2 ) от пункта A до места их встречи. Графики зависимости координаты автомобилей от времени изображены на рис. 6. Здесь tg = v1 , а tg = v2< 0, т. к. v2 направлена в сторону, противоположную направлению принятому за
положительное. Моменту встречи соответствует точка C пересечения графиков.
Ответ: tC |
= |
|
L |
, а |
xC |
= |
lv1 |
. |
||
v1 |
v2 |
v1 |
v2 |
|||||||
|
|
|
|
|
|
|||||
7. Понятие ускорения
Однако движение любого тела в реальных условиях никогда не бывает строго равномерным и прямолинейным. В большей степени оно, как правило, неравномерное. Поскольку при неравномерном поступательном движении скорость тела изменяется с течением времени, то для количественного процесса изменения скорости тела вводят ещё одну величину – ускорение.
7.1 Среднее ускорение
Среднее ускорение – это отношение изменения скорости к промежутку времени, за который это изменение произошло.
Определить среднее ускорение можно формулой: |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
= |
v = |
v v0 |
, |
|
(17) |
||
|
|
|
|
|
v0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ср |
|
t |
|
t2 t1 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
направление вектора ускорения совпадает |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
с |
направлением |
изменения |
|
вектора |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v |
|
|
||||||||||||
|
|
|
|
|
|
|
v |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
скорости |
v = v v0 |
( v0 это |
начальная |
||||||||||
|
|
|
v |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
aср |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
скорость, то есть скорость, с которой тело |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
начало |
ускоряться). |
|
В |
момент времени |
|||||||
|
t1 |
|
t |
|
|
t2 |
|
|
t |
|
||||||||||||||||||
|
|
|
|
|
|
t1 |
(рис. |
7) |
тело |
имеет |
скорость |
v0 , в |
||||||||||||||||
|
|
|
|
|
|
|
Рис. 7 |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
момент времени t2 скорость v. |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7.2. Мгновенное ускорение |
|
|
|
|
||||||||
|
По |
определению |
мгновенным |
ускорением |
называется |
векторная |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
равная |
пределу |
отношения |
малого |
изменения |
вектора |
|||||||||||||||
величина a , |
||||||||||||||||||||||||||||
2015, ЗФТШ МФТИ, Чивилёв Виктор Иванович Паркевич Егор Вадимович
10
