Curve

называется соприкасающаяся плоскостью исходной кривой в точке r0. Начальная точка M0(r0) и направляющие векторы r00 è r000 составляют внутреннюю систему координат этой плоскости.

Соприкасающаяся плоскость не меняется при допустимой замене параметра. Действительно,

Поэтому при замене параметра вектор второй производной умножается на положительный множитель и получает приращение, коллинеарное касательной. Это означает, что при любом выборе параметра конец этого вектора (отложенного от точки на кривой) лежит в одной и той же полуплоскости соприкасающейся плоскости. Назовем эту полуплоскость

положительной.

Кривая, определяемая уравнением (3), лежит в соприкасающейся плос-

кости и определяется в ее внутренней системе координат уравнением u2 = 2v. Такой вид имеет уравнение параболы, если начало координат

на параболе, одна из осей ее касается, а вторая ось параллельна оси параболы. Оно является каноническим уравнением, если система координат декартова прямоугольная.

В отличие от касательной, парабола меняется при замене параметра.

Действительно, внутренняя система координат соприкасающейся плоскости меняется, а уравнение u2 = 2v остается неизменным. Значит, это

уравнение в новой системе координат определяет новую параболу. Постараемся выбрать в соприкаса-

ющейся плоскости декартову прямоугольную систему координат, естественно связанную с кривой в окрестности выбранной точки. Для этого выберем на кривой параметр s так, чтобы

dr

(Дифференцирование по s вместо штриха будем обозначать точкой сверху.) Тогда

dds(r; r) = 2(r; •r) = 0;

и вектор •r ортогонален r.

9

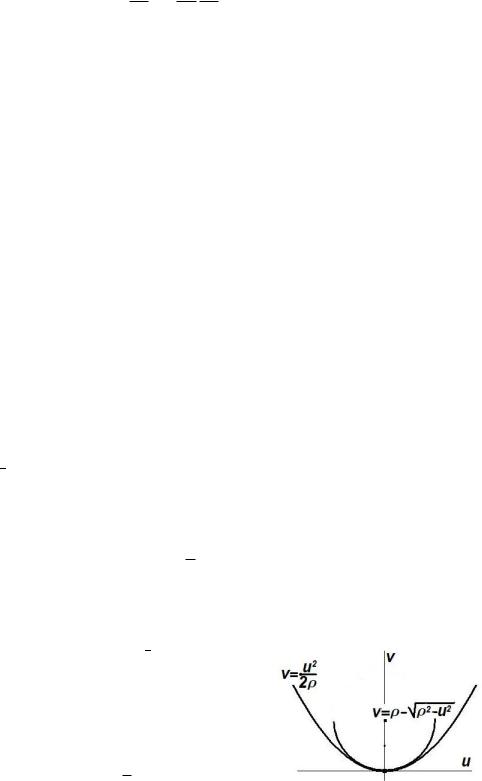
Такой выбор параметра всегда возможен. Действительно, при замене

параметра

ddrt = ddsr ddst :

Поэтому, если на кривой выбран некоторый параметр t 2 [ ; ], то необходимо (и достаточно), чтобы js0tj = jr0tj. Сохраняя ориентацию кривой,

В качестве s(t) выберем ту первообразную функции jr0tj, которая удовлетворяет условию s( ) = 0: Легко видеть, что эта функция строго

монотонная и дважды непрерывно дифференцируемая, а значит такая замена является допустимой.

Параметр s называется натуральным параметром. Натуральный па-

раметр определен однозначно. Действительно, если s и s1 = '(s) два натуральных параметра, то jr0sj = jr0s1 j j'0(s)j = 1, è '0(s) = 1, если ориентация кривой не менялась. Следовательно, s1 = s + C, à C = 0, åñëè

оба параметра равны нулю в начальной точке кривой.

В курсе доказывается, что при выборе в качестве параметра переменной длины дуги длина вектора производной тождественно равна единице. Это выясняет геометрический смысл натурального параметра.

Перейдем к натуральному параметру. Вектор

•r ортогонален r, но длина его, вообще говоря, отлична от 1. Величина

k = j•r(s0)j

называется кривизной кривой в данной точке, а вектор n = k1•r

вектором главной нормали. Его длина равна 1, и он направлен в положительную полуплоскость соприкасающейся плоскости.

Это означает, что базис t = r0; n = •r0=j•r0j

ортонормированный, и уравнение соприкаса-

ющейся параболы, соответствующей натуральному параметру, при таком базисе канониче- ское. Уравнение (3) запишется как

r(u; v) = r0 + t s + 12k n s2;

Ðèñ. 3

10

и мы видим, что парабола имеет уравнение v = (1=2)ku2 èëè u2 = 2 v; где = 1=k. Коэффициент называется радиусом кривизны.

Для объяснения этого названия сравним параболу v = u2=(2 ) и окружность радиуса , проходящую через вершину параболы (рис. 3): u2 + (v )2 = 2. Та полуокружность, которая проходит через нача-

Отсюда видно, что окружность и парабола отличаются друг от друга на бесконечно малую не менее, чем третьего порядка относительно u = s.

Окружность с уравнением u2 +(v )2 = 2, где радиус кривизны,

называется соприкасающейся окружностью, а ее центр центром кривизны. Итак, пренебрегая бесконечно малыми третьего порядка, можно считать, что точка движется по окружности радиуса , лежащей в со-

прикасающейся плоскости.

Выясним геометрический (кинематический) смысл кривизны. То, что на кривой выбран натуральный параметр s 2 [0; S], означает, что ко-

нец вектора r(s) проходит кривую с линейной скоростью, равной 1. При этом, как мы видели, с точностью до бесконечно малых третьего порядка

можно считать, что точка кривой движется по соприкасающейся окруж-

!

ности. Ее угловая скорость ! направлена перпендикулярно плоскости вращения, то есть соприкасающейся плоскости. Так как j!j j j

! = t = 1,

мы видим, что

j!j

! = k:

Пренебрегая малыми третьего порядка, мы считаем движение точки круговым. При этом вектор t поворачивается, оставаясь перпендикуляр-

ным радиусу, и угловая скорость его вращения равна угловой скорости

!

вращения радиуса, то есть ! . Заметим, что вектор t поворачивается в сторону положительной полуплоскости соприкасающейся плоскости, то есть по направлению к вектору n. Это значит, что направление его

вращения видно против часовой стрелки из того полупространства, в которое направлено векторное произведение [t; n].

11

Вектор b = [t; n] называется вектором бинормали. Он имеет длину

1 и направлен перпендикулярно соприкасающейся плоскости, образуя правую тройку с t и n. Так как r = t и •r = kn, мы видим, что

• ! kb = [r; r] = ! :

Èòàê,

вектор kb может интерпретироваться как угловая скорость

вращения касательной при движении точки по кривой с линейной скоростью, равной 1.

Еще одна геометрическая интерпретация кривизны может быть полу- чена так. Найдем расстояние от конца вектора r(s0+ s) до касательной. Оно равно

(7)

Этот же результат можно усмотреть и из формулы (6).

Вы- числения при натуральном параметре, конечно, просты, но переход к натуральному параметру, как правило затруднителен. Поэтому полезны следующие формулы.

1. Нормальная плоскость. Радиус-вектор начальной точки r0, íîð- мальный вектор r00. Уравнение

(r r0; r00) = 0:

2. Соприкасающаяся плоскость. Радиус-вектор начальной точки r0, направляющие векторы r00 è r000. Уравнение

(r r0; r00; r000) = 0:

12

5. Спрямляющая плоскость. Радиус-вектор начальной точки r0, íà- правляющие векторы r00 è [r00; r000]. Уравнение:

(r r0; r00; [r00; r000]) = 0 èëè (r r0; n) = 0:

6. Для вычисления кривизны найдем еще раз расстояние h, получен-

Найденное h совпадает с (7) потому что речь идет о расстоянии до ка-

сательной от одной и той же точки, координаты которой представлены как функции параметров s и t:

Разделим обе части равенства на s2 и перейдем к пределу при s ! 0. При этом необходимо учесть, что

В результате мы получим

j[r0 ; r00]j

k = 0 0 : jr00j3

Для плоской кривой, заданной уравнениями x = x(t); y = y(t) эта формула принимает вид

jy00x0 y0x00j

k = (x02 + y02)3=2 :

7. Центр кривизны. Его радиус-вектор получается как

rc = r0 + n:

Получим координаты центра кривизны для плоской кривой, заданной уравнениями x = x(t) и y = y(t). Мы найдем нормальный вектор n, если повернем касательный вектор r0(x0; y0) на прямой угол и разделим

на его длину. Но необходимо выбрать направление поворота так, чтобы угол между повернутым вектором и вектором r00(x00; y00) был острым.

13

Рассмотрим вектор a с координатами ( ( y0); x0), где = 1. Оче- видно, что (r0; a) = 0. Потребуем, чтобы (r00; a) было положительно:( y0x00 + x0y00) > 0. Это определяет как = sgn (y00x0 x00y0). Вектор a необходимо пронормировать, то есть разделить на (x02 + y02)1=2,

умножить на радиус кривизны = 1=k, и отложить полученный вектор от точки с радиус-вектором r(x; y). Это позволяет написать следующие координаты центра кривизны:

Очевидные упрощения приводят к формулам

5. Формулы Френе. Лучи, направленные по векторам t, n и b

составляют трехгранный угол, называемый трехгранником Френе. Ча- сто так же называют и ортонормированный базис, составленный из этих векторов. Векторы t, n и b зависят от параметра, и трехгранник пово-

рачивается при движении точки. Поэтому его называют также сопровождающим трехгранником. Формула

жения производных от остальных векторов.

Для этого напомним сначала, что компоненты произвольного вектора в ортонормированном базисе e1; e2; e3 это его скалярные произведения на соответствующие базисные векторы. По определению ортонормированного базиса (ei; ej) = 0 ïðè i 6= j, è (ei; ei) = 1. Дифференцируя эти равенства, получаем

(e0i; ej) + (ei; e0j) = 0 è 2(e0i; ei) = 0;

14

то есть производная каждого вектора ему ортогональна, а, например, компонента производной первого вектора по второму отличается знаком от компоненты производной второго вектора по первому.

Принимая во внимание эти соображения и равенство (8), мы можем написать

Эти формулы называются формулами Френе. Единственный незнакомый нам объект в этих формулах это функция { = {(s), называ-

åìàÿ кручением кривой. Кручение определяется третьей производной от радиус-вектора точки по параметру, если, конечно, эта производная существует. Оно характеризует отклонение точки от исходной соприкасающейся плоскости, при ее смещении по кривой на s. Действительно,

рассмотрим расстояние от точки с радиус-вектором r = r(s0 + s) до плоскости, соприкасающейся с кривой в точке r0 = r(s0). Оно равно

или после упрощений

p = 16 s3j(v; b)j + o( s3);

Обратим внимание на то, что кручение, в отличие от кривизны, может принимать отрицательные значения. Его знак показывает, в какую сторону от соприкасающейся плоскости смещается точка кривой.

Чтобы получить выражение кручения через произвольный параметр вычислим еще раз то же расстояние с учетом знака:

15

Разделим равенство

(r0; r00; r000) t3 + o( t3) = {k s3 + o( s3)

j[r0; r00]j

íà s3 и перейдем к пределу при s ! 0 также, как это делалось при вычислении кривизны:

(r0; r00; r000)

{k = j[r0; r00]j jr0j3 :

6.Кривизна и кручение характеризуют кривую в целом.

Это означает, что задание непрерывно дифференцируемых функций k = k(s) > 0 и { = {(s) для s 2 [0; S] определяет кривую с точностью до

положения в пространстве.

Объясним, откуда это следует. Если к формулам Френе мы добавим равенство r = t, то получится система из четырех векторных уравнений,

выражающих производные от четырех векторов как линейные комбинации этих векторов с коэффициентами заданными функциями. Такая система есть сокращенная запись объединения трех систем линейных дифференциальных уравнений (для каждой из компонент).

В курсе обыкновенных дифференциальных уравнений доказывается теорема (теорема существования и единственности решения задачи Коши для линейных систем), согласно которой существует и притом единственное решение r = r(s), t = t(s), n = n(s), b = b(s) рассматриваемой

системы уравнений, удовлетворяющее начальным условиям r(0) = r0, t(0) = t0, n(0) = n0, b(0) = b0, ãäå r0, t0, n0 è b0 могут быть заданы произвольно.

Начальные условия задают положение в пространстве трехгранника Френе, соответствующего начальной точке. После этого кривая определяется кривизной и кручением однозначно.

16