Сложность

Большинство встречающихся в природе звуков невозможно представить простой синусоидальной волной, аналогичной той, что изображена на рис. 12.2. Звук, соот­ветствующий по своим свойствам идеальной синусоиде с постоянной частотой и амплитудой, может быть получен лишь в лабораторных условиях. Большинство звуков, которые мы слышим в реальной жизни, — это сочетания акустических сиг­налов, каждый из которых может быть представлен своей собственной синусоидой, вследствие чего их общая, суммарная, синусоида отличается сложностью. Так, большинство окружающих нас звуков — голоса людей и животных, шум, донося­щийся с улиц, забитых транспортными средствами, звуки музыкальных инстру­ментов и т. п. — это результат взаимного наложения различных волн с разными частотами. Для подобных звуков характерны чрезвычайно сложные циклы изме­нений давления — циклы сжатия и разрежения (рис. 12.6).

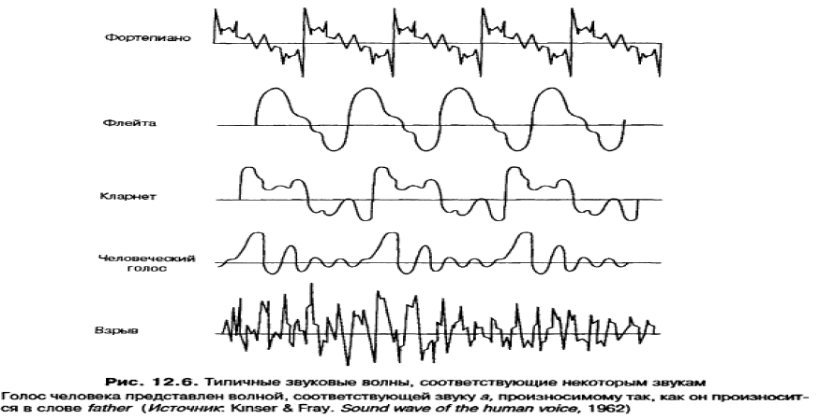
В сложных звуковых волнах, создаваемых музыкальными инструментами, про­является важное свойство источников звуковых колебаний Как правило, любой источник сложных звуковых колебаний одновременно создает звуковые волны с разными частотами. Самые низкие частоты, называемые фундаментальной часто­той (или первой гармоникой), определяют высоту сложного звука Задетая скри­пичная или гитарная струна колеблется как единое целое, вызывая чередование сжатий и разрежений окружающего ее воздуха Однако колебания создает не толь­ко вся струна целиком (что является источником фундаментальной частоты), од­новременно звуковые волны генерируются и отдельными участками струны, пред­ставляющими собой строго определенные доли ее общей длины (рис. 12.7).

Эти дополнительные колебания с частотами, кратными фундаментальной ча­стоте, называются гармониками (или обертонами). Иными словами, фундамен­тальная частота представляет собой самую низкую частоту сложной звуковой волны; все более высокие частоты, кратные частоте фундаментальной волны, пред­ставляют собой гармоники последней. Роль фундаментальной частоты и ее гармо­ник будет рассмотрена ниже, в разделе, посвященном патологии слуха.

Сложные волны и анализ Фурье. Несмотря на то что сложный звук не может быть представлен в виде одной синусоидальной волны, его можно представить несколькими синусоидами. Вспомните то, что было сказано про анализ Фурье в главе б при обсуждении анализа сложных визуальных сцен их разложением на простые синусоидальные волны. Аналогичным образом анализируются и звуковые волны. Не вдаваясь в детали, можно сказать, что, согласно теореме Фурье, любая сложная периодическая волна может быть представлена в виде суммы ряда про­стых синусоидальных волн, каждая их которых имеет свои собственные частоту и амплитуду. Разложение сложной волны любой формы на компоненты, имеющие синусоидальную форму, называется анализом Фурье. Синтез волн, имеющих сложные формы, из простых синусоидальных волн называется синтезом Фурье.

В качестве примера синтеза сложной волны рассмотрим рис. 12.8. Источником приблизительно такой квадратной волны, полный цикл которой представлен в пра­вом нижнем углу рис. 12.8, бывают некоторые сирены. Анализ этого звука, выпол­ненный по методу Фурье, показал, что он образован пятью компонентами, пред­ставленными в левой колонке рис. 12.8. Правая колонка — сложные волны, образующиеся в результате последовательного добавления компонентов (на каждом этапе добавляется по одной волне). Математически анализ Фурье начинается с фундаментальной частоты — самой низкой частоты из всех, представленных в сложной волне. Именно к ней добавляются синусоидальные волны, более высо­кие частоты которых кратны фундаментальной частоте.

Высота сложного тона определяется его фундаментальной частотой. Если ис­пытуемому предъявить сложный звук, а затем попросить его подобрать простой звук, соответствующий ему по высоте, то он выберет звук, который можно пред­ставить простой синусоидой с частотой, примерно равной фундаментальной частоте сложного звука. Иными словами, высота сложного тона приблизительно рав­на высоте звука, который можно представить синусоидой с частотой, близкой к фундаментальной частоте сложного тона (Мооге, 1994).

Акустический закон Ома. Аудиальная система может, правда лишь приблизи­тельно, анализировать сложные волны по методу Фурье: она разлагает их на со­ставляющие компоненты и направляет информацию о представленных в ней час­тотах на более высокие уровни аудиальной системы. Этот феномен, известный под названием акустического закона Ома (названного в честь немецкого физика Геор­га Ома (1787-1854), более известного своими работами в области электричества заключается в следующем: когда на нас воздействует относительно сложный звук, например когда мы слышим аккорд, образованный несколькими нотами, мы спо­собны оценить вклад, внесенный в него отдельно каждой нотой Иными словами, из закона Ома следует, что мы способны воспринимать индивидуальные частот­ные компоненты сложного звука.

Тембр. Психологическим аспектом восприятия звука, отражающим сложность звуковой волны, является тембр (от старофранцузского слова tamber, что значит «маленький колокольчик»). Тембр — это отличительное качество тона того или иного звука, являющееся результатом числа и интенсивности гармоник (или обер­тонов), которые производит этот звук Например, сложный звук музыкального инструмента образован фундаментальной частотой и обертональными частотами, всегда кратными фундаментальной частоте и присутствующими в звуке в разных количествах. Количество и характер обертонов, создаваемых разными музыкаль­ными инструментами, различны, вследствие чего различны и тембры. Именно бла­годаря тембру мы отличаем музыкальные инструменты друг от друга даже тогда, когда звучат одни и те же ноты одинаковой высоты. Различия в тембрах музыкаль­ных инструментов — следствие различий их обертонов.

Подводя итог, можно сказать, что высота сложного звука зависит в первую оче­редь от его фундаментальной частоты, а тембр — от гармоник. Именно поэтому такие инструменты, как гитара и фортепиано, создающие много обертонов, обла­дают и более наполненным, богатым звуком, нежели инструменты, издающие от­носительно чистый, однородный звук (в частности, флейта).