
- •Теория автоматического управления
- •Рецензент кандидат технических наук, доцент кафедры автоматики и телемеханики фгбоу впо «ВятГу» в. Н. Поздин
- •Общие вопросы
- •1.1. Цель и задачи лабораторного практикума
- •1.2. Общие методические указания
- •2. Частотные характеристики и переходные процессы в сау
- •Программа самостоятельной работы
- •Программа работ в лаборатории
- •2.1.3. Методические указания к работе № 1
- •Вопросы для самоконтроля
- •Литература
- •2.2.1. Цель работы
- •2.2.2. Задание к работе
- •2.2.3. Методические указания к лабораторной работе № 2
- •Вопросы для самопроверки
- •Программа работы в лаборатории
- •3.1.3. Методические указания к лабораторной работе № 3
- •Вопросы для самоконтроля
- •3.2. Лабораторная работа № 4. Система с параллельным корректирующим устройством
- •3.2.1. Цель работы
- •3.2.2. Задание к работе
- •Программа самостоятельной работы
- •Программа работы в лаборатории
- •3.2.3. Методические указания к лабораторной работе № 4
- •Вопросы для самопроверки
- •4.1.3. Методические указания к лабораторной работе № 5
- •Вопросы для самопроверки
- •4.2. Лабораторная работа № 6. Система с импульсным элементом
- •4.2.1. Цель работы
- •4.2.2. Задание к работе
- •Программа самостоятельной работы
- •4.2.3. Методические указания к лабораторной работе № 6
- •Вопросы для самопроверки
- •Библиографический список
- •Теория автоматического управления
Вопросы для самопроверки
1. По структурной схеме НСАУ пояснить процесс появления автоколебаний.
2. Какова причина того, что в НСАУ с двухзвенным фильтром амплитуда автоколебаний выше, чем в системе с однозвенным фильтром?
3. Как меняется
![]() и
и![]() при
изменении параметровa
и в
нелинейного звена?
при
изменении параметровa
и в
нелинейного звена?
Литература
[2, c.138–154, 232–235];
[3, c.290–302, 311–317];
[4, c.251–258].
Рис.
12. Структурная схема и параметры НСАУ
к лабораторной
работе № 5 Рис.
13. Определение параметров автоколебаний
в НСАУ с двухзвенным
фильтром


4.2. Лабораторная работа № 6. Система с импульсным элементом
4.2.1. Цель работы
И
![]()
![]()

 зучить
влияние импульсного элемента на динамику
замкнутой системы регулирования.
Убедиться в существовании придельной
частоты среза непрерывной части системы,
зависящей от периода следования
импульсов, выше которой замкнутая
система при наличии импульсного элемента
становится неустойчивой или колебательной.
зучить
влияние импульсного элемента на динамику
замкнутой системы регулирования.
Убедиться в существовании придельной
частоты среза непрерывной части системы,
зависящей от периода следования
импульсов, выше которой замкнутая
система при наличии импульсного элемента
становится неустойчивой или колебательной.
Р![]() ис.
14. Структурная схема к лабораторной
работе № 6
ис.
14. Структурная схема к лабораторной
работе № 6
4.2.2. Задание к работе
Таблица 5
|
Вариант |
|
|
|
|
|
|
|
|
|
|
|
1-1 1-2 1-3 |
0.1 0.1 0.1 |
10 |
2 2 2 |
1 1 1 |
1 1 1 |
1 0 1 |
0.052 0.052 0.052 |
0.1 0.1 0.1 |
0.176 0.176 0.176 |
0.91 0.91 0.91 |
|
2-1 2-2 2-3 |
0.1 0.1 0.1 |
10 |
3 3 3 |
1 1 1 |
1 1 1 |
1 0 1 |
0.052 0.052 0.052 |
0.1 0.1 0.1 |
0.088 0.088 0.088 |
1.91 1.91 1.91 |
|
3-1 3-2 3-3 |
0.2 0.2 0.2 |
10 |
4 4 4 |
1 1 1 |
1 1 1 |
1 0 1 |
0.052 0.052 0.052 |
0.2 0.2 0.2 |
0.088 0.088 0.088 |
1.91 1.91 1.91 |
|
4-1 4-2 4-3 |
0.1 0.1 0.1 |
10 |
3 3 3 |
1 1 1 |
1 1 1 |
1 0 1 |
0.052 0.052 0.052 |
0.1 0.1 0.1 |
0.088 0.088 0.088 |
0.91 0.91 0.91 |
Программа самостоятельной работы
1. Построить
аппроксимированные ЛАЧХ разомкнутой
САУ с параметрами, приведёнными на рис.
12. Определить частоту
![]() среза системы. При построении импульсный
элемент учитывать безынерционным звеном
с коэффициентом передачи, равным.
среза системы. При построении импульсный
элемент учитывать безынерционным звеном
с коэффициентом передачи, равным.
2. Из числа набираемых
на наборном поле значений
![]() подобрать ближайшее меньшее значение,
при котором
подобрать ближайшее меньшее значение,
при котором![]() .
.
3. Построить ЛАЧХ и переходную функцию замкнутой САУ.
Программа работы в лаборатории
1. Собрать исследуемую систему на наборном поле.
2. На экране
компьютера просмотреть и зарисовать
переходные процессы на выходе САУ при
подаче ступенчатого входного воздействия
![]() для
различных значений
для
различных значений![]() .
Определить предельную величину
.
Определить предельную величину![]() ,
при которой замкнутая импульсная система
становится неустойчивой или колебательной.
Сопоставить экспериментальные данные
с расчётом.
,
при которой замкнутая импульсная система
становится неустойчивой или колебательной.
Сопоставить экспериментальные данные
с расчётом.
3. Объяснить полученные результаты.
4.2.3. Методические указания к лабораторной работе № 6
Исследуемая
импульсная САУ состоит из импульсного
элемента – звена 4 и аналоговых элементов.
Звенья 1, 3 – апериодические; звено 2 –
апериодическое с постоянной времени
![]() приk1
или интегрирующее с постоянной времени
приk1
или интегрирующее с постоянной времени
![]() приk1
=
, звено 5 – безынерционное с коэффициентом
связи 1 при
приk1
=
, звено 5 – безынерционное с коэффициентом
связи 1 при
![]() или пропорционально – интегрирующее
с постоянной времениТ4
при
или пропорционально – интегрирующее
с постоянной времениТ4
при![]() и
и![]()
![]() .
Импульсный элемент выдаёт импульсы
через период, равный
.
Импульсный элемент выдаёт импульсы
через период, равный![]() .
Продолжительность импульса в долях
периода
.
Продолжительность импульса в долях
периода![]() (скважность импульса) равна.
Высота импульса равна ординате сигнала
(скважность импульса) равна.
Высота импульса равна ординате сигнала
![]() на входе элемента 4.
на входе элемента 4.
В соответствии с
теоремой Котельникова, замкнутую
импульсную систему можно рассматривать
как линейную непрерывную систему с
учётом импульсного элемента в виде
безынерционного звена с передаточным
коэффициентом
при условии, что частота среза
![]() не превышает предельного значения
не превышает предельного значения![]() .
.
При
![]() наличие в системе импульсного элемента
практически не отражается на переходных
процессах в замкнутой системе, если не
принимать во внимание наложенные на
кривую переходного процесса пульсации
периода следования импульсов. При этом
амплитуда пульсации тем меньше, чем
меньше значение
наличие в системе импульсного элемента
практически не отражается на переходных
процессах в замкнутой системе, если не
принимать во внимание наложенные на
кривую переходного процесса пульсации
периода следования импульсов. При этом
амплитуда пульсации тем меньше, чем
меньше значение![]() .
.
При
![]() наличие импульсного элемента может
привести к неустойчивости замкнутой
системы.
наличие импульсного элемента может
привести к неустойчивости замкнутой
системы.
Аппроксимированную
ЛАЧХ
![]() САУ в разомкнутом состоянии рекомендуется
строить ускоренно в следующем порядке:
САУ в разомкнутом состоянии рекомендуется
строить ускоренно в следующем порядке:
определить наклон ЛАЧХ в области низких частот, определяемый наличием или отсутствием идеальных дифференцирующих и интегрирующих звеньев. В варианте 1 присутствует одно интегрирующее звено 1/T2p c эквивалентным коэффициентом усиления
 ,
в варианте 2 – два интегрирующих звена
1/T2p
и
,
в варианте 2 – два интегрирующих звена
1/T2p
и
 и
и ,
в варианте 3 – интегрирующее и
дифференцирующее звенья отсутствуют
и
,
в варианте 3 – интегрирующее и
дифференцирующее звенья отсутствуют
и .
Таким образом, в области низких частот
ЛАЧХ отсекает на оси ординат отрезок,
равный
.
Таким образом, в области низких частот
ЛАЧХ отсекает на оси ординат отрезок,
равный ,
и идёт в вариантах 1, 2, 3 с наклоном,
соответственно –1, –2, 0 лог/дек;
,
и идёт в вариантах 1, 2, 3 с наклоном,
соответственно –1, –2, 0 лог/дек;
найти частоты сопряжения
 сомножителей вида
сомножителей вида иTip+1;
иTip+1;последовательно по мере возрастания
 изменять наклон
изменять наклон на –1 лог/дек для сомножителей
вида
на –1 лог/дек для сомножителей
вида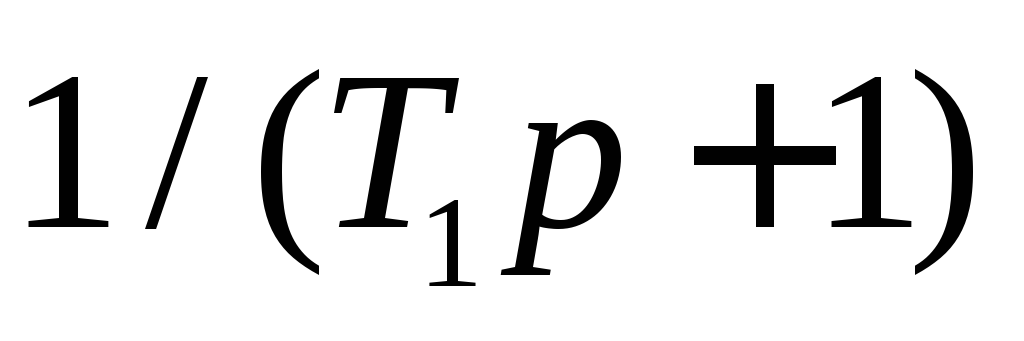 и на + 1 лог/дек для сомножителей видаTip+1;
и на + 1 лог/дек для сомножителей видаTip+1;абсцисса, в которой
 ,
определяет частоту
,
определяет частоту среза САУ. ЛАЧХ замкнутой САУ может
быть найдена упрощённо по
аппроксимированной
среза САУ. ЛАЧХ замкнутой САУ может
быть найдена упрощённо по
аппроксимированной с
учётом поправок при
с
учётом поправок при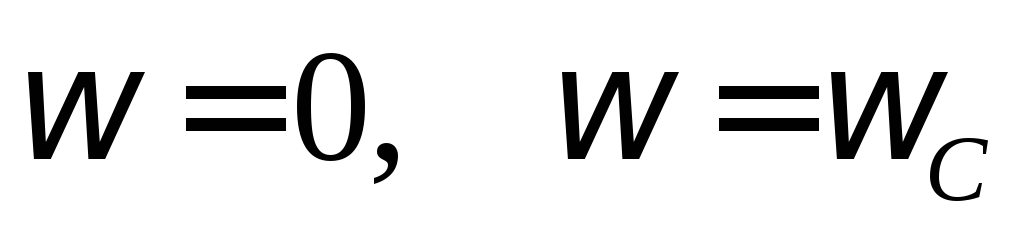 .
.
