
- •Конспект лекций
- •2. Основные операции над матрицами
- •Тема 2 Определители и их свойства.
- •1. Определители и их свойства
- •2. Ранг матрицы
- •3. Обратная матрица
- •Тема 3. Элементы линейной алгебры в экономике
- •1. Линейная модель международной торговли
- •2. Модель Леонтьева многоотраслевой экономики
- •Тема 4 Системы линейных алгебраических уравнений
- •1. Системы линейных алгебраических уравнений. Теорема Кронекера Капелли
- •2. Применение определителей к исследованию и решению систем линейных уравнений. Формулы Крамера
- •1. Решение систем линейных алгебраических уравнений методом обратной матрицы
- •2. Решение систем линейных алгебраических уравнений методом Гаусса
- •Тема 5 Элементы векторной алгебры
- •1. Векторы. Координаты вектора
- •2. Линейные операции над векторами
- •3. Скалярное и векторное произведение векторов
- •Тема 6. Элементы высшей алгебры
- •Тема 7 Элементы аналитической геометрии
- •1. Уравнение линии на плоскости
- •2. Прямая линия на плоскости
- •3. Полярные координаты
- •1. Канонические уравнения эллипса, гиперболы, параболы
- •2. Преобразования декартовой системы координат на плоскости
2. Линейные операции над векторами
Сумма
векторов
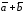 есть вектор
есть вектор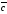 ,
соответствующий их геометрической
сумме (правило
параллелограмма)
(рис. 4.10).
Из рис. 4.10
видно, что если конец вектора
,
соответствующий их геометрической
сумме (правило
параллелограмма)
(рис. 4.10).
Из рис. 4.10
видно, что если конец вектора
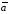 совмещен (параллельным перемещением)
с началом вектора
совмещен (параллельным перемещением)
с началом вектора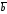 ,
то вектор
,
то вектор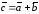 будетсоединять
начало вектора
будетсоединять
начало вектора
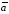 с концом вектора
с концом вектора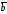 .
.
Вычитание
векторов
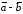 есть сумма вектора
есть сумма вектора
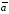 с вектором (
с вектором (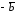 ),
который противоположен вектору
),
который противоположен вектору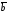 :
: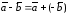 (рис. 4.11).
(рис. 4.11).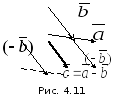
Если
векторы
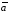 и
и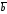 заданы своими координатами:
заданы своими координатами: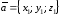 ,
,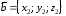 ,
то
,
то
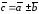 =
=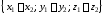 .
(4.5)
.
(4.5)
Вектор
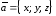 можно
представить в виде суммы трех его
компонент по координатным осям (рис. 4.7):
можно
представить в виде суммы трех его
компонент по координатным осям (рис. 4.7):
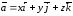 (4.6)
(4.6)
Эта
сумма называется разложением
вектора по базисным векторам (базису).
Отсюда следует, что координаты вектора
– это коэффициенты
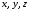 в разложении (4.6)
вектора по базисным векторам.
в разложении (4.6)
вектора по базисным векторам.
Произведение
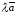 вектора
вектора
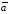 на скаляр
(число)
на скаляр
(число)
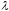 есть вектор, который коллинеарен вектору
есть вектор, который коллинеарен вектору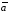 ,
имеет длину
,
имеет длину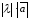 и направлен в ту же
сторону, что
и вектор
и направлен в ту же
сторону, что
и вектор
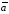 ,
если
,
если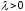 ,
и в противоположную сторону, если
,
и в противоположную сторону, если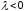 .
Если вектор задан своими координатами:
.
Если вектор задан своими координатами: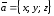 ,
то
,
то
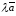 =
=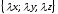 .
(4.7)
.
(4.7)
Сложение
векторов и умножение их на скаляры
удовлетворяют соотношениям (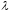 и
и – числа):
– числа):
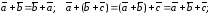
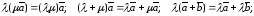
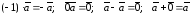 .
.
Пример.
Найти координаты вектора
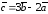 ,
если
,
если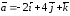 ,
,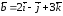 .
.
◄ По
заданным разложениям векторов по базису
находим их координаты:
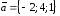 ,
,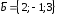 .
Используя (4.5) и (4.7), получаем
.
Используя (4.5) и (4.7), получаем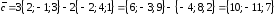 ►
►
3. Скалярное и векторное произведение векторов
Скалярное
произведение двух векторов
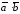 (обозначают также
(обозначают также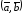 )
есть скаляр (число)
)
есть скаляр (число)
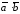 =
=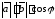 ,
(4.8)
,
(4.8)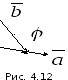
где
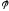 – угол между векторами
– угол между векторами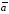 и
и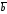 (рис. 4.12).
(рис. 4.12).
Для
острого угла между векторами
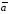 и
и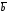 их скалярное произведение
их скалярное произведение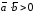 ,
а для тупого –
,
а для тупого –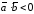 .
Если они взаимно перпендикулярны
.
Если они взаимно перпендикулярны
(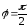 ),
то
),
то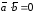 .
Для коллинеарных векторов
.
Для коллинеарных векторов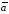 и
и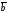 скалярное произведение
скалярное произведение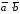 =
=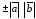 ,
где “+” для однонаправленных векторов,
а “–“ ― для противоположно направленных.
В частности
,
где “+” для однонаправленных векторов,
а “–“ ― для противоположно направленных.
В частности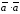 =
=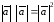 ,
что позволяет записать длину вектора
,
что позволяет записать длину вектора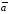 в виде
в виде =
=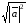 (отсюда другое
название длины вектора – «модуль
вектора»).
(отсюда другое
название длины вектора – «модуль
вектора»).
Единичные
базисные векторы прямоугольной декартовой
системы координат удовлетворяют
соотношениям:
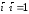 ,
,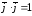 ,
,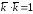 ,
,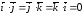 .
Используя эти соотношения, не трудно
получить, что если векторы
.
Используя эти соотношения, не трудно
получить, что если векторы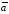 и
и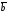 заданы своими декартовыми координатами:
заданы своими декартовыми координатами: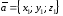 ,
,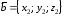 ,
то их скалярное произведение
,
то их скалярное произведение
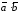 =
=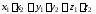 .
(4.9)
.
(4.9)
Из определения скалярного произведения (4.8) следует, что угол между векторами
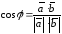 .
(4.10)
.
(4.10)
Свойства скалярного произведения:
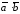 =
= ;
;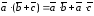 ;
;
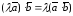 ;
;
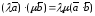 ;
;
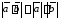 .
.
Пример.
Вычислить
 ,
если
,
если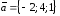 ,
,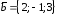 .
.
◄ Используя
свойства скалярного произведения, имеем
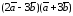 =
=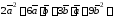

=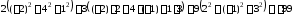 .►
.►
Пример.
Даны координаты вершин треугольника
на плоскости:
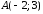 ,
,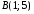 ,
,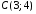 .
Найти угол в треугольнике при вершине
.
Найти угол в треугольнике при вершине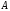 и длину стороны
и длину стороны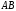 .
.
◄ Проведем
из вершины
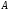 векторы в вершины
векторы в вершины и
и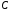 (рис. 4.13).
Тогда угол
(рис. 4.13).
Тогда угол
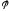 при вершине
при вершине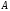 будет равен углу между векторами
будет равен углу между векторами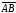 и
и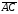 ,
а длина стороны
,
а длина стороны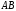 равна длине вектора
равна длине вектора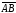 .
Находим координаты векторов:
.
Находим координаты векторов: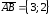 ,
,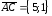 .
Согласно формуле (.10)
.
Согласно формуле (.10)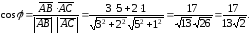 Длина
стороны
Длина
стороны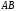 =
=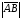 =
=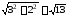 .
►
.
►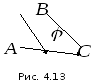
Векторное
произведение
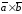 (другое обозначение
(другое обозначение
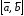 )
двух векторов
)
двух векторов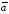 и
и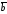 есть третий вектор
есть третий вектор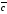 ,
модуль которого
,
модуль которого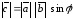 (т. е. равен площади параллелограмма,
построенного на векторах
(т. е. равен площади параллелограмма,
построенного на векторах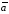 и
и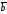 ),
а направление перпендикулярно к обоим
векторам
),
а направление перпендикулярно к обоим
векторам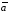 и
и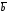 (т. е. плоскости упомянутого параллелограмма)
и совпадает с направлением поступательного
движения правого винта при его повороте
от
(т. е. плоскости упомянутого параллелограмма)
и совпадает с направлением поступательного
движения правого винта при его повороте
от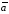 к
к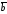 на угол, меньший
на угол, меньший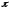 (рис 4.14).
Из этого определения векторного
произведения следует, что векторы
(рис 4.14).
Из этого определения векторного
произведения следует, что векторы
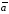 ,
,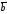 и
и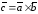 образуютправую
систему.
образуютправую
систему.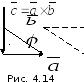
Если
векторы
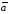 и
и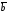 коллинеарны (
коллинеарны (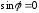 ),
то
),
то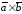 =0.
=0.
Свойства векторного произведения:
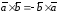 ;
;
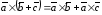 ;
;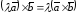 ;
;
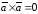 ;
;
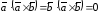 .
.
Базисные единичные векторы декартовой прямоугольной системы координат удовлетворяют следующим соотношениям:
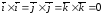 ;
;
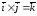 ;
;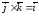 ;
;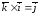 .
.
Если
векторы
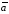 и
и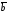 заданы своими декартовыми координатами:
заданы своими декартовыми координатами: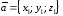 ,
,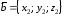 ,
то их векторное произведение
,
то их векторное произведение
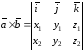 .
(4.11)
.
(4.11)
Смешанным
(векторно – скалярным) произведением
векторов
называется
произведение
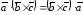 ,
результатом которого является скаляр
(число). Для компланарных векторов их
смешанное произведение
,
результатом которого является скаляр
(число). Для компланарных векторов их
смешанное произведение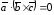 .
Если векторы
.
Если векторы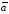 ,
,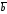 и
и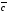 образуют правую тройку, то
образуют правую тройку, то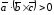 ,
если – левую, то
,
если – левую, то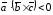 .
.
Смешанное
произведение
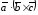 равно объему параллелепипеда
равно объему параллелепипеда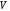 ,
построенного на векторах
,
построенного на векторах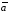 ,
,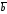 и
и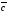 (рис. 4.15),
взятому со знаком “+”, если векторы
(рис. 4.15),
взятому со знаком “+”, если векторы
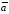 ,
,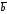 и
и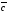 образуют правую тройку, и со знаком “–“,
если ― левую:
образуют правую тройку, и со знаком “–“,
если ― левую: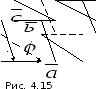
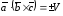 .
(4.12)
.
(4.12)
Если
векторы
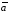 ,
,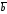 и
и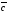 заданы своими декартовыми координатами:
заданы своими декартовыми координатами: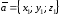 ,
,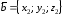 ,
,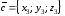 ,
то их смешанное произведение
,
то их смешанное произведение
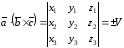 (4.13)
(4.13)
Пример.
Даны координаты вершин треугольника:
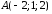 ,
,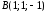 ,
,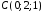 .
Найти площадь
.
Найти площадь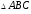 .
.
◄ Направим
из вершины
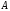 треугольника векторы в вершины
треугольника векторы в вершины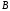 и
и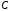 (рис. 4.16).
Учитывая, что площадь
(рис. 4.16).
Учитывая, что площадь
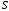
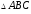 равна половине площади параллелограмма,
построенного на этих векторах, площадь
которого, в свою очередь, можно выразить
через векторное произведение, будем
иметь
равна половине площади параллелограмма,
построенного на этих векторах, площадь
которого, в свою очередь, можно выразить
через векторное произведение, будем
иметь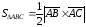 .
Находим координаты векторов:
.
Находим координаты векторов: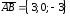 ,
,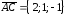 .
По формуле (4.11) находим векторное
произведение
.
По формуле (4.11) находим векторное
произведение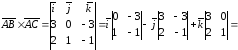
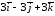 =
=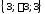 .
.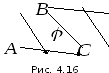
Таким
образом,
 (кв. ед.). ►
(кв. ед.). ►
Пример.
Найти объем параллелепипеда, построенного
на векторах
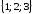 ,
, ,
,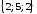 .
.
◄ Искомый
объем найдем по формуле (4.13). Вычисляем
смешанное произведение данных векторов:
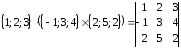 =
=
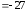 .
Объем параллелепипеда
.
Объем параллелепипеда
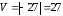 .
►
.
►
